В алгебре существует множество методов и операций для решения различных математических задач. Один из таких методов — куб разности. Куб разности представляет собой специальную операцию, которая позволяет найти куб разницы двух чисел. Этот метод имеет свои особенности, которые важно понимать для правильного применения. В данной статье мы рассмотрим определение куба разности и расскажем о его особенностях. Благодаря этому вы сможете более эффективно использовать этот метод в своих математических вычислениях и задачах.
- Определение и особенности куба разности в алгебре
- Определение куба разности
- Способы вычисления куба разности
- Метод разностей кубов
- Метод формулы разности кубов
- Таблица разностей кубов
- Примеры использования куба разности
- 1. Расчет изменения объема
- 2. Оценка изменения показателей
- 3. Определение величины изменений в экспериментах
- Куб разности в алгебре: определение и особенности
Определение и особенности куба разности в алгебре
Куб разности обладает рядом особенностей, которые делают его интересным и полезным средством в алгебре.
- Раскрытие скобок: По свойству куба разности, его можно раскрыть с помощью формулы разности кубов. Таким образом, (а — b)^3 = а^3 — 3а^2b + 3ab^2 — b^3. Это позволяет упростить алгебраические выражения и решать уравнения, связанные с кубами разности.
- Сокращение: Если значения а и b равны, то куб разности становится нулем: (а — а)^3 = 0. Это свойство позволяет сокращать выражения и находить значения переменных, при которых куб разности равен нулю.
- Взаимосвязь с другими алгебраическими операциями: Куб разности связан с другими алгебраическими операциями, такими как квадрат разности и разность кубов. Это позволяет использовать эти операции вместе для решения сложных задач и упрощения выражений.
Использование куба разности в алгебре позволяет решать уравнения, моделировать реальные ситуации и анализировать математические отношения на более высоком уровне. Он помогает углубить понимание алгебры и развить навыки аналитического мышления.
Итак, куб разности в алгебре – это мощный инструмент, который помогает упрощать выражения, находить значения переменных и решать сложные математические задачи. Используйте его с уверенностью и наслаждайтесь его применением в вашем образовании и повседневной жизни.
Определение куба разности
Когда мы говорим о кубе разности, мы имеем в виду математическую операцию, которая применяется к разности двух чисел.
Рассмотрим пример: у нас есть два числа, а и b. Их разницу обозначим как (a-b). Если мы возведем эту разность в куб, то получим куб разности и обозначим его как (a-b)^3.
Что же происходит, когда мы возводим куб разности в куб? Мы получаем куб куба разности, что записывается как ((a-b)^3)^3, то есть (a-b)^9.
Таким образом, куб разности — это возведение в куб разности двух чисел, а куб куба разности — это возведение в куб куба разности.
- Пример 1: Пусть a=5 и b=2. Тогда куб разности будет равен (5-2)^3=3^3=27.
- Пример 2: Пусть a=7 и b=4. Тогда куб разности будет равен (7-4)^3=3^3=27.
Куб разности имеет несколько особенностей. Например, его значение всегда будет положительным, если только разность двух чисел не равна нулю.
Также стоит упомянуть, что куб κ разности (a-b)^κ всегда будет симметричен относительно оси координат. Это означает, что его график будет выглядеть одинаково независимо от знака значений a и b.
Итак, теперь вы знаете, что такое куб разности. Эта математическая операция позволяет нам рассчитывать значение куба разности двух чисел и имеет несколько интересных особенностей. Она может применяться в различных областях математики и науки, а также в повседневной жизни.
Способы вычисления куба разности
В алгебре существуют различные методы и формулы для вычисления куба разности. Представлю несколько из них ниже:
Метод разностей кубов
Этот метод основан на разложении разности кубов на сумму трех слагаемых:
(a — b)(a^2 + ab + b^2) = a^3 — b^3
где a и b — любые числа.
Данный метод позволяет сократить количество операций и упростить вычисление куба разности.
Метод формулы разности кубов
Этот метод основан на формуле разности кубов:
(a — b)^3 = a^3 — 3a^2b + 3ab^2 — b^3
где a и b — любые числа.
Для вычисления куба разности по этому методу необходимо вычислить каждое слагаемое по формуле и затем сложить их результаты.
Таблица разностей кубов
Для упрощения вычислений можно использовать таблицу разностей кубов. В этой таблице представлены значения кубов от 1 до 10, а также разности кубов для каждой пары чисел.
| Число | Куб | Разность кубов |
|---|---|---|
| 1 | 1 | 0 |
| 2 | 8 | 7 |
| 3 | 27 | 19 |
| 4 | 64 | 52 |
| 5 | 125 | 100 |
| 6 | 216 | 160 |
| 7 | 343 | 236 |
| 8 | 512 | 408 |
| 9 | 729 | 648 |
| 10 | 1000 | 900 |
При использовании таблицы разностей кубов можно быстро и точно определить значение куба разности для любых двух чисел от 1 до 10.
В приведенных выше способах вычисления куба разности каждый из них имеет свои преимущества и может быть использован в различных ситуациях. Выбор метода зависит от конкретной задачи и удобства его применения.
Примеры использования куба разности
1. Расчет изменения объема

Предположим, у вас есть куб с изначальным объемом 10 кубических сантиметров. Затем, вы увеличиваете размер всех его сторон на 2 сантиметра. Чтобы узнать, насколько увеличился объем куба, вы можете воспользоваться кубом разности.
Для этого нужно вычислить разницу объемов двух кубов: первого с изначальными размерами и второго с увеличенными размерами. Куб разности позволит вам найти эту разницу и узнать, насколько увеличился объем куба. В данном случае, куб разности будет равен 8 кубическим сантиметрам (12^3 — 10^3 = 1728 — 1000 = 728).
2. Оценка изменения показателей
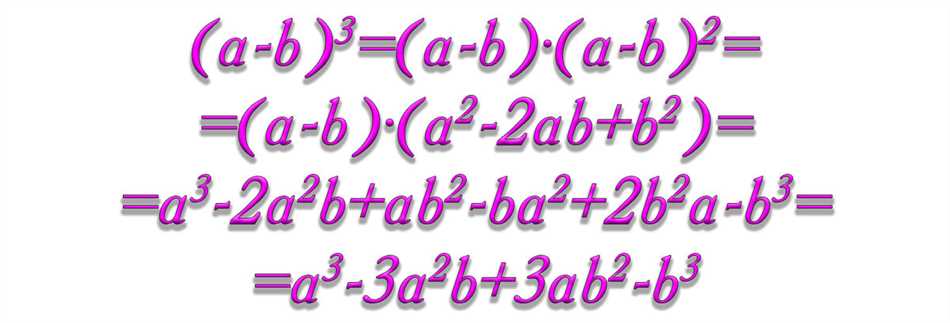
Куб разности можно использовать для оценки изменения показателей в различных областях. Например, представьте, что у вас есть набор данных о выручке вашей компании за последние три года. Чтобы узнать, как сильно увеличилась выручка с первого на третий год, можно применить куб разности.
Вы можете вычислить разницу в выручке за первый и третий год, используя куб разности. Это позволит вам понять, насколько значительно выросла ваша выручка за указанный период и сделать оценку изменения показателей.
3. Определение величины изменений в экспериментах
Куб разности также можно применять в научных экспериментах для оценки влияния изменений на определенную величину. Представьте, что вы проводите эксперимент, меняя температуру воздуха в помещении и измеряя скорость реакции.
Все эти примеры демонстрируют разнообразные применения куба разности в различных областях. Он является одним из основных инструментов для анализа изменений и оценки их влияния.
Куб разности в алгебре: определение и особенности
Формула для куба разности имеет следующий вид:
(a — b)(a^2 + ab + b^2) = a^3 — b^3
Где a и b – любые числа или алгебраические выражения.
Особенностью куба разности является возможность его факторизации. Исходную формулу можно переписать в следующем виде:
a^3 — b^3 = (a — b)(a^2 + ab + b^2)
Это означает, что можно разложить куб разности двух выражений на произведение разности их значений и суммы квадратов их значений.
Куб разности часто используется в алгебре для упрощения выражений, решения уравнений и доказательства тождеств.