Квадрат в математике: определение и особенности

Квадрат – это одна из самых основных геометрических фигур, которая широко используется в математике. Квадрат обладает всеми свойствами, которые характерны для геометрических фигур: у него есть стороны, углы, периметр и площадь. Но квадрат имеет также свои уникальные особенности. Во-первых, все стороны квадрата равны между собой, что делает его особенно симметричным и гармоничным. Во-вторых, все углы в квадрате равны 90 градусам, что делает его прямоугольным. Квадраты находят применение не только в геометрии, но и в алгебре, физике и других областях науки.

Определение

Определение квадрата может показаться очевидным, но глубже изучая эту фигуру, мы можем обнаружить, что она имеет множество уникальных и важных особенностей.

Во-первых, одной из главных характеристик квадрата является равенство всех его сторон. Это означает, что длина каждой стороны одинакова и может быть обозначена через букву «a».

Другой особенностью квадрата является то, что его диагонали равны и пересекаются в точке, называемой центром квадрата. Диагональ квадрата может быть вычислена с использованием теоремы Пифагора, так как она является гипотенузой прямоугольного треугольника с катетами, равными длине сторон квадрата.

Квадрат также обладает симметрией. Это означает, что его можно разделить пополам вдоль любой из его диагоналей, и обе полученные части будут зеркально отражать друг друга.

Квадрат можно найти в множестве аспектов жизни. В архитектуре квадратные формы могут использоваться для создания стабильных и симметричных структур. В природе некоторые организмы, такие как некоторые виды бактерий или сотовые структуры, могут иметь форму квадрата.

Также квадрат является одним из основных понятий в алгебре и геометрии. В алгебре квадрат может относиться к процессу, в результате которого число умножается на себя. В геометрии квадрат является базовой фигурой для изучения пространственных взаимосвязей и вычислений.

В общем, квадрат — это не просто геометрическая фигура, но и концепция, которую мы можем встретить везде вокруг нас. Он символизирует симметрию, стабильность и гармонию, и его математические свойства помогают нам понять множество аспектов нашего мира.

Свойства квадрата

1. Равные стороны и углы

В квадрате все стороны равны друг другу. Это означает, что длина каждой стороны одинакова. А значит, если ты знаешь длину одной стороны, ты легко можешь найти длину остальных.

Также у квадрата все углы прямые и равны между собой. Это отличает его от других многоугольников, где углы могут быть разными.

2. Диагонали

У квадрата есть две диагонали — это отрезки, которые соединяют противоположные вершины. Интересно, что диагонали в квадрате равны и пересекаются под прямым углом.

Зная длину одной диагонали, ты можешь найти длину другой, используя теорему Пифагора.

3. Площадь и периметр

Площадь квадрата вычисляется по формуле: сторона квадрата в квадрате. Если ты знаешь длину стороны, ты можешь легко найти площадь квадрата.

Периметр квадрата вычисляется по формуле: длина стороны умноженная на 4. Это сумма всех сторон квадрата. Если ты знаешь длину одной стороны, ты можешь найти периметр квадрата.

4. Симметрия

Квадрат обладает симметрией. Это означает, что его можно разделить на две равные половины с помощью прямой линии. Каждая половина будет точно такой же, как и другая.

5. Обратимость

Квадрат можно также назвать обратимой фигурой. Это означает, что если ты знаешь площадь квадрата, ты можешь найти длину его стороны. И наоборот, если ты знаешь длину стороны квадрата, ты можешь найти его площадь.

Квадрат — это уникальная фигура с интересными и полезными свойствами. Надеюсь, теперь ты лучше понимаешь, что такое квадрат и почему он так важен в математике. Попробуй использовать эти свойства на практике и посмотри, как они могут помочь тебе в решении различных задач.

Квадратное уравнение

Такое уравнение называется квадратным, потому что переменная x в нем возводится в квадрат. Мы часто встречаемся с квадратными уравнениями в математике, физике и других науках, а также в реальном мире.

Используя квадратные уравнения, мы можем решать различные задачи, например, находить корни уравнений, определять вершину параболы и решать задачи о движении объектов.

Одна из особенностей квадратного уравнения — то что оно имеет два корня. Корни — это значения x, при которых уравнение равняется нулю.

Формула для нахождения корней квадратного уравнения называется формулой дискриминанта:

x = (-b ± √(b^2 — 4ac)) / 2a

Здесь √(b^2 — 4ac) — это квадратный корень из дискриминанта. Если дискриминант положителен, то у уравнения есть два различных корня. Если дискриминант равен нулю, то у уравнения есть только один корень. Если дискриминант отрицателен, то у уравнения нет действительных корней.

Когда мы решаем квадратное уравнение, мы на самом деле находим значения x, при которых уравнение равно нулю. Корни квадратного уравнения могут быть как действительными числами, так и комплексными числами.

Решая квадратные уравнения, мы развиваем наши навыки в алгебре и математике в целом. Эти навыки могут быть полезными в нашей повседневной жизни, например, при решении задач по финансам, инженерии или программированию.

Теперь, когда вы знаете, что такое квадратное уравнение и как его решать, вы можете применить эти знания к различным задачам и упражнениям. Удачи в изучении математики!

Площадь и периметр

Периметр — это длина границы фигуры, то есть сумма всех сторон. Для примера, давайте представим, что у нас есть четырехугольник. Чтобы найти периметр этого четырехугольника, нужно сложить длины всех его сторон. Если у нас есть квадрат, то периметр будет равен удвоенной сумме длин его сторон, так как все стороны четрыехугольника равны.

Среди простых шагов нахождения периметра квадрата можно выделить следующие:

1. Запишите значения всех сторон квадрата. Назначьте букву a одной их них, это значение будет представлять все стороны, так как все стороны равны.
2. Сложите значения всех сторон. У нас только одна сторона, значит результатом будет a+a+a+a.
3. Сократите формулу, объединив одинаковые значения, чтобы получить окончательный ответ. В итоге формула будет выглядеть как 4a.

Площадь — это мера площади внутри фигуры или поверхности. Для прямоугольных фигур, таких как квадрат, площадь можно найти, умножив длину одной стороны на длину другой стороны. Если все стороны квадрата равны, то площадь будет равна стороне, возводимой в квадрат.

Шаги нахождения площади квадрата:

1. Запишите значение длины одной из сторон квадрата. Назначьте букву a этому значению.
2. Возводите эту сторону в квадрат, умножая ее на саму себя. Результатом будет a * a.
3. Упростите выражение, если это возможно. В итоге получим площадь квадрата.

Итак, периметр и площадь — это два ключевых понятия, которые помогают нам лучше понять форму и размеры фигур. Понимание этих понятий помогает не только в математических расчетах, но и в повседневной жизни. Например, зная площадь комнаты, мы можем определить, сколько квадратных метров ковра нам понадобится. А понятие периметра поможет нам правильно оценить количество материала, необходимого для изготовления ограды.

Диагонали и диагональные отрезки

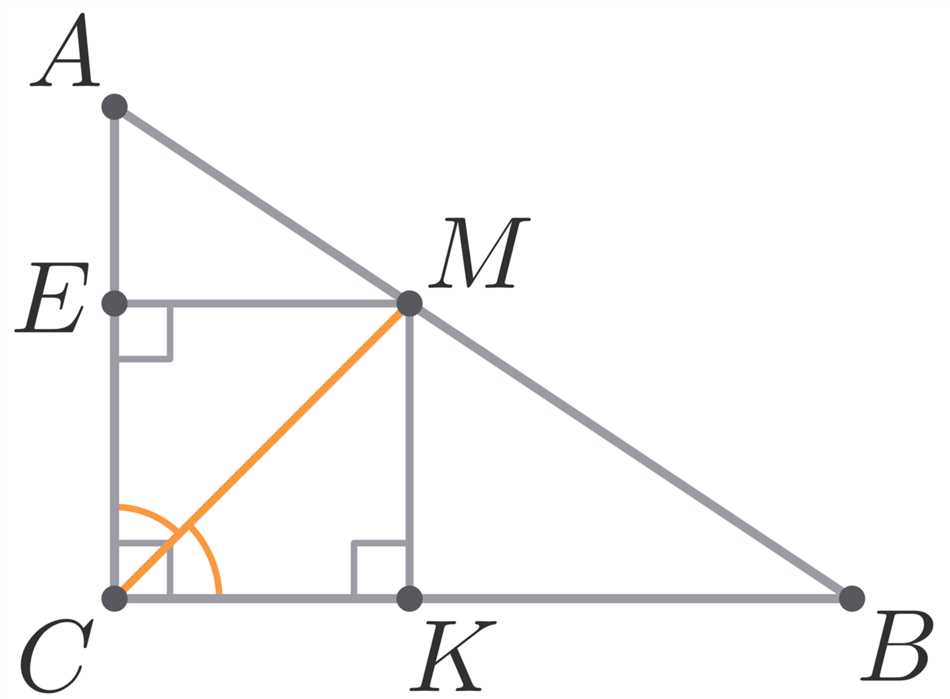
Обратимся к простому квадрату, где все стороны равны друг другу. Диагонали в этом случае являются равными отрезками, а значит, могут быть использованы для различных математических вычислений и конструкций. Когда диагонали разделяют квадрат на два треугольника, каждый из этих треугольников является прямоугольным. Таким образом, наличие диагоналей делает квадрат особенным и позволяет использовать его в различных задачах.

Диагонали также имеют другую интересную особенность — они являются биссектрисами углов квадрата. Это означает, что каждая диагональ делит углы квадрата пополам. Если у нас есть квадрат с углом 90 градусов, то диагональ будет делить этот угол на два угла по 45 градусов. Это означает, что диагонали не только соединяют противоположные углы, но и позволяют делить углы на равные части.

Кроме того, диагонали также имеют значение в геометрии квадрата. Они являются единственными линиями, которые делят квадрат на две равные части, и вместе с сторонами образуют прямоугольник. Это означает, что диагонали являются основными элементами, которые помогают определить форму и размеры квадрата.

Когда мы говорим о диагоналях и диагональных отрезках, мы подразумеваем различные концепции и свойства, которые связаны с квадратом. Диагонали не только соединяют углы и делят углы на равные части, но и являются основными элементами, определяющими форму и размеры квадрата. Они предоставляют возможность для математических вычислений и конструкций, а также добавляют интригу в изучение геометрии квадрата.

Способы нахождения площади и периметра

Нахождение площади квадрата

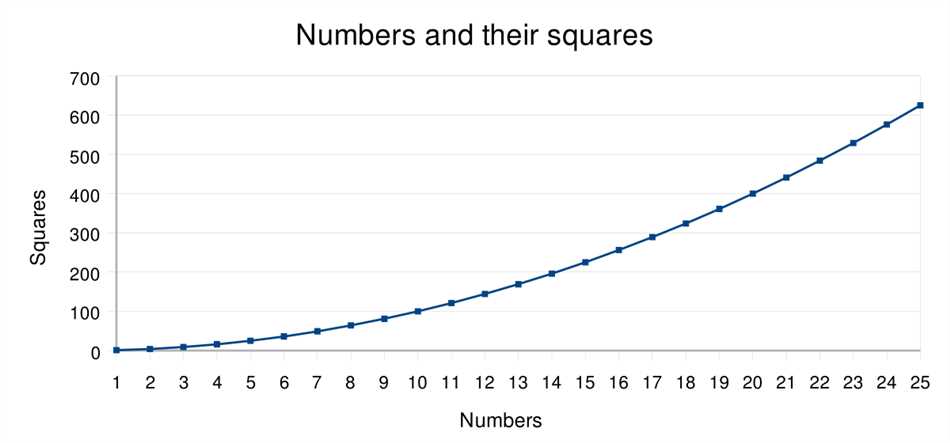
Площадь квадрата — это количество площадных единиц, которые могут поместиться внутри фигуры. Чтобы найти площадь квадрата, нам нужно знать длину одной его стороны (обозначим ее как «a»). Формула для нахождения площади квадрата проста и прямолинейна: площадь равна квадрату длины стороны.

Формула: S = a²

Так что если длина стороны квадрата составляет, например, 5 единиц, то его площадь будет равна 5² = 25 квадратным единицам.

Нахождение периметра квадрата

Периметр квадрата — это сумма длин всех его сторон. Для нахождения периметра квадрата, нам также нужно знать длину одной его стороны (обозначим ее также как «a»). Так как все стороны квадрата одинаковы, мы можем просто умножить длину одной стороны на 4.

Формула: P = 4a

Например, если длина стороны квадрата равна 7 единицам, то его периметр будет равен 4 * 7 = 28 единицам.

Можно заметить, что в формулах для нахождения площади и периметра квадрата присутствует длина его стороны. Поэтому, чтобы найти один из этих параметров, мы должны знать длину стороны квадрата. И наоборот, если мы знаем площадь или периметр квадрата, то можем вычислить длину его стороны.

Теперь, когда вы знаете, как найти площадь и периметр квадрата, вы можете использовать эти формулы для решения задач и нахождения параметров квадратов в реальной жизни. Например, если у вас есть участок земли формой квадрата, вы можете использовать эти формулы для определения его площади и периметра. Или если вы строите раму для фотографии и хотите, чтобы она была в форме квадрата, вы можете использовать формулы для нахождения размеров рамы.

Так что не бойтесь математики и используйте эти простые формулы для нахождения площади и периметра квадрата — они помогут вам решить множество задач и легко разобраться в этой теме!

Квадрат в математике: определение и особенности

Особенности квадрата:

1. Равные стороны: Все стороны квадрата равны друг другу. Это значит, что если одна сторона квадрата имеет длину a, то все остальные стороны также будут иметь длину a.
2. Равные углы: Все углы квадрата равны 90 градусам. Квадрат является прямоугольником, так как все его углы прямые.
3. Диагонали: В квадрате существуют две диагонали, которые соединяют противоположные вершины. Диагонали квадрата равны друг другу и пересекаются в середине.
4. Периметр и площадь: Периметр квадрата вычисляется как сумма длин всех его сторон, а площадь — как квадрат длины одной из его сторон.

Таким образом, квадрат является одной из основных геометрических фигур и имеет ряд особенностей, которые делают его уникальным и полезным в математике и в реальном мире.