Квадрат – одна из самых важных и изучаемых фигур в математике. Он состоит из четырех сторон и четырех углов, которые все равны между собой. Главная особенность квадрата – все его стороны имеют одинаковую длину, а углы равны 90 градусам.
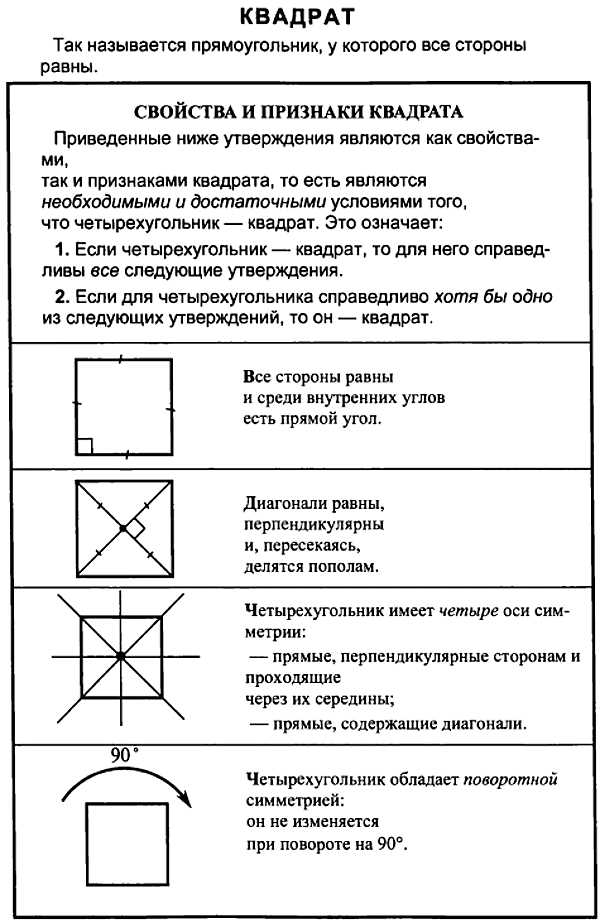
Квадрат обладает несколькими значимыми свойствами. Во-первых, его площадь можно легко вычислить, умножив длину одной из его сторон на саму себя. Во-вторых, он является регулярным многоугольником, что означает, что все его углы и стороны равны. Квадрат также имеет центр симметрии и четыре оси симметрии, что делает его особенно интересным в геометрических расчетах и конструкциях.
Изучение квадрата является фундаментальным для понимания различных математических концепций и применений, таких как алгебра, геометрия и теория вероятностей.
Определение квадрата
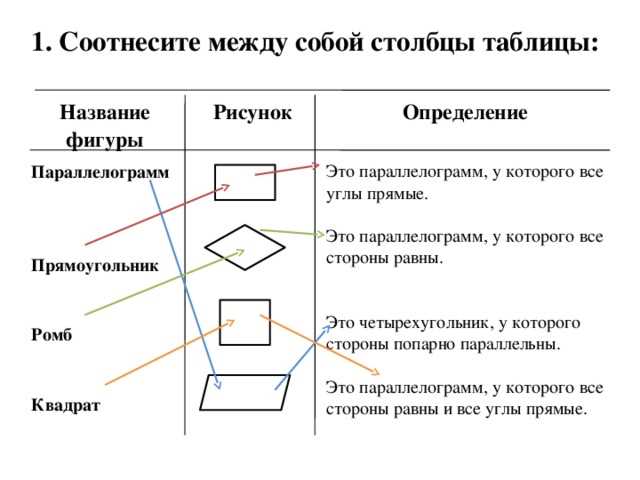
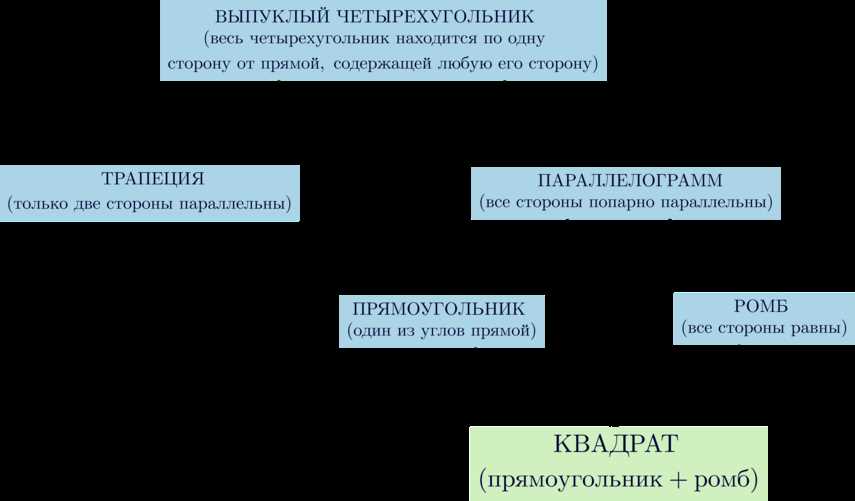
У квадрата есть несколько способов определения. Во-первых, его можно определить как регулярный четырехугольник, у которого все стороны и углы одинаковы. Другими словами, квадрат — это прямоугольник, у которого все стороны равны. Второе определение состоит в том, что квадрат можно рассматривать как специальный случай ромба, у которого все углы прямые.
Квадрат обычно обозначается символом «□». Например, если у нас есть квадрат со стороной 5 единиц, то его можно записать как «□ ABCD», где A, B, C и D — вершины квадрата, а сторона AB имеет длину 5 единиц.
Квадрат имеет несколько важных характеристик. Во-первых, периметр квадрата равен сумме длин всех его сторон. Для квадрата со стороной a, периметр P можно выразить формулой P = 4a. Во-вторых, площадь квадрата равна произведению длины его стороны на саму себя. Для квадрата со стороной a, площадь S можно выразить формулой S = a * a или S = a^2.
Квадрат также имеет множество других свойств и особенностей, которые помогают в его изучении и использовании в различных областях науки, техники и повседневной жизни. Например, квадрат обладает симметрией относительно своих диагоналей, и его диагонали являются радиусами вписанной окружности. Квадраты также широко используются в алгебре и геометрии для моделирования различных задач и расчетов.
Пространственные представления квадратов

Когда мы думаем о квадратах, обычно представляем себе двумерные фигуры на плоскости. Однако, квадраты могут быть представлены не только на плоскости, но и в трехмерном пространстве.
Возьмем, например, комнату. Комната может иметь форму куба, где каждая стена является квадратом. Представьте себе, как каждая сторона комнаты равна другой и каждый угол образует прямой угол. Эти свойства делают комнату квадратной в трехмерном пространстве.
Также можно представить квадраты в трехмерном пространстве, используя геометрические фигуры, такие как кубы и параллелепипеды. Каждая грань куба или параллелепипеда является квадратом.
Когда мы начинаем исследовать квадраты в трехмерном пространстве, возникают новые свойства и возможности. Например, можно разместить квадратный объект на плоскости, а затем повернуть его в трехмерном пространстве для создания кубической фигуры.
Это лишь некоторые примеры пространственного представления квадратов. В реальном мире мы встречаем эти фигуры повсюду, от зданий и мебели до упаковочных материалов и игрушек. Квадраты в трехмерном пространстве предоставляют нам новые возможности для творчества и конструирования.
Площадь квадрата
Площадь квадрата — это просто и в то же время очень важное понятие в математике. Она помогает нам измерять поверхности и понимать, сколько места занимает объект.
Ты, наверное, знаешь, что квадрат — это фигура, у которой все стороны равны. Из-за этого квадрат имеет много интересных свойств. Одно из них — равенство всех углов, они равны 90 градусам.
Чтобы найти площадь квадрата, нужно знать длину его стороны. Возьми линейку и измерь сторону квадрата. Представим, что длина стороны равна 5 сантиметрам. Теперь умножь эту длину на саму себя: 5 * 5 = 25. Получается, площадь квадрата равна 25 квадратным сантиметрам.
Продолжим нашу прогулку по этому удивительному месту. Видишь квадрат со стороной 7 сантиметров? Какая же будет его площадь? Правильно, нужно умножить 7 на 7: 7 * 7 = 49. Получается, площадь такого квадрата равна 49 квадратным сантиметрам.
Один из самых интересных фактов о площади квадрата заключается в том, что она всегда положительна. Можешь ли ты представить себе квадрат со стороной, равной -3 сантиметра? Если ты попытаешься построить такой квадрат на бумаге, то, скорее всего, это не получится. Квадрат всегда имеет положительную площадь.
Класс! Теперь ты знаешь, что такое площадь квадрата и как ее узнать. В следующий раз, когда увидишь квадрат, можешь посчитать его площадь и похвастаться своими математическими навыками своими друзьями.
Периметр квадрата
Поскольку все стороны квадрата равны, вычислить его периметр очень просто. Достаточно умножить длину одной стороны на 4.
Формула периметра квадрата:
P = 4a
Где P — периметр квадрата, a — длина стороны квадрата.
Например, если сторона квадрата равна 5 сантиметров, то его периметр будет выглядеть следующим образом:
P = 4 * 5 = 20 сантиметров.
Таким образом, периметр квадрата равен 20 сантиметров, если его сторона равна 5 сантиметров.
Периметр квадрата — это важная характеристика данной фигуры. Он позволяет нам оценить размеры и длину всех его сторон. Знание периметра квадрата полезно при решении задач из геометрии и арифметики.
Благодаря своей простоте вычисления и пониманию, периметр квадрата является одним из первых понятий, которые мы изучаем в школьной программе по математике. В его основе лежит понятие длины стороны и умножение чисел.
Таким образом, периметр квадрата — это сумма его четырех сторон, которая определяется формулой P = 4a. Знание периметра квадрата помогает нам лучше понять геометрические особенности данной фигуры и применять его в решении различных задач.
Диагонали квадрата
В квадрате существует всего две диагонали — это отрезки, которые соединяют противоположные вершины квадрата. Диагональ можно представить как воображаемую линию, которая проходит через центр квадрата и делит его на два равных треугольника. Таким образом, диагонали в квадрате обладают несколькими интересными и полезными свойствами.
Уже само определение диагоналей подразумевает их равенство. Диагонали квадрата равны друг другу по длине. Это утверждение является основополагающим свойством квадрата, и оно может быть использовано для решения различных задач, например, для нахождения стороны квадрата по его диагонали или для нахождения площади квадрата.
Кроме того, диагонали квадрата делят его на четыре равных прямоугольных треугольника. В каждом из этих треугольников один из углов всегда является прямым — 90 градусов. Таким образом, мы можем утверждать о наличии прямоугольных треугольников внутри квадрата, без каких-либо дополнительных знаний о его стороне или углах.
Квадрат в математике: определение и свойства
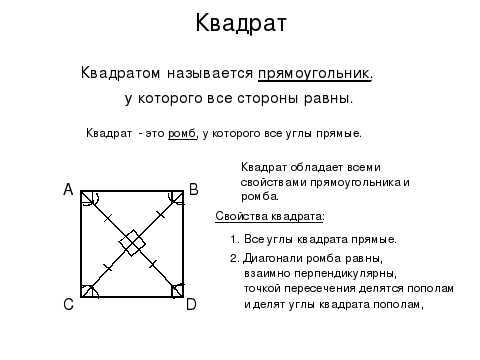
Квадратом называется геометрическая фигура, образованная четырьмя одинаковыми сторонами, которые образуют прямые углы между собой. Каждый угол квадрата равен 90 градусам.
Основные свойства квадрата:
- Все стороны квадрата равны между собой.
- Все углы квадрата равны между собой и равны 90 градусам.
- Диагонали квадрата равны между собой и перпендикулярны друг другу.
- Периметр квадрата равен сумме длин всех его сторон: P = 4a, где a — длина стороны квадрата.
- Площадь квадрата равна квадрату длины его стороны: S = a^2, где a — длина стороны квадрата.
Квадрат является одной из основных геометрических фигур и широко применяется в математике и других научных областях.