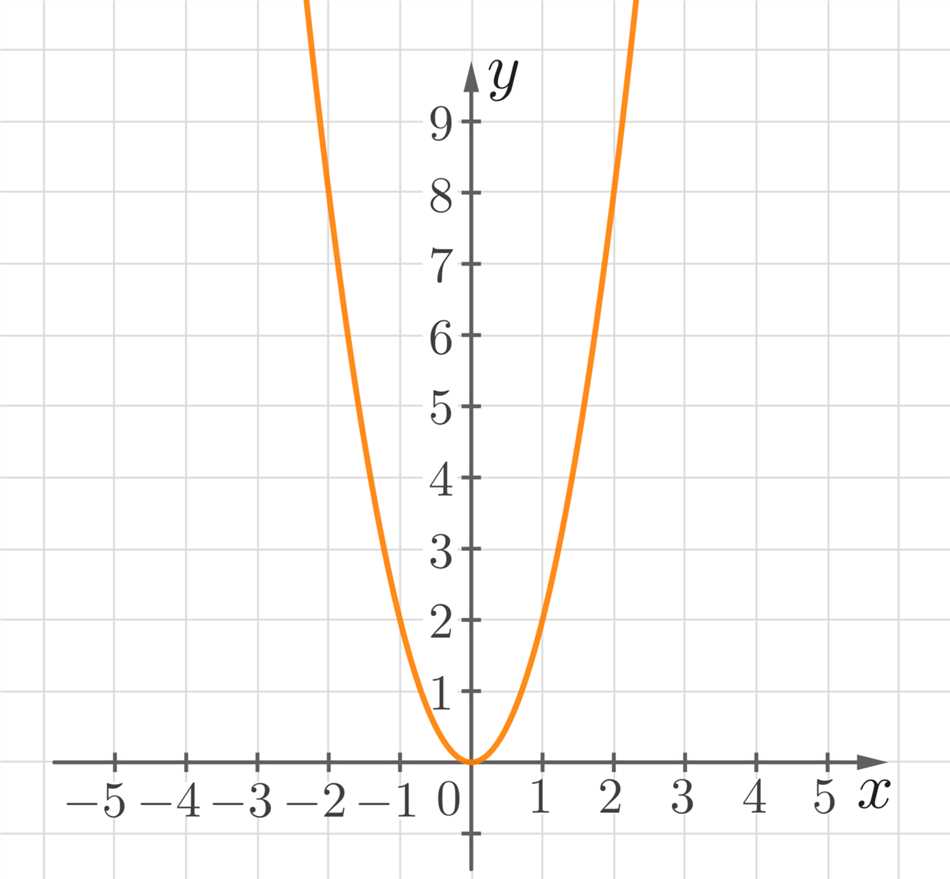
Когда мы говорим о квадратичной зависимости, мы имеем в виду математическую модель, в которой одна переменная зависит квадратично от другой. Это означает, что при увеличении значения одной переменной, вторая переменная увеличивается в квадрате. Такая зависимость может найти применение в различных областях, от экономики до физики.
Принцип работы квадратичной зависимости основан на квадратном законе. Чем выше значение одной переменной, тем более сильно возрастает значение другой переменной. Это может быть полезно для анализа различных явлений и предсказания их развития.
Например, квадратичная зависимость может наблюдаться в физике при изучении падения тела. График зависимости времени от расстояния будет иметь параболическую форму, что указывает на квадратичную зависимость между этими переменными.
Определение

Концепция квадратичной зависимости имеет широкое применение в различных областях, таких как физика, экономика, биология и технические науки. Она используется для анализа и предсказания различных явлений и процессов.
Квадратичная зависимость может быть представлена в виде математического уравнения, которое включает квадрат переменной. Например, уравнение квадратичной зависимости может иметь вид:
y = a*x^2 + b*x + c
где y — зависимая переменная, x — независимая переменная, a, b и c — коэффициенты, определяющие форму и положение кривой.
Примером квадратичной зависимости может служить связь между временем и расстоянием, которую может проделать объект, движущийся с постоянным ускорением. Если время удваивается, расстояние изменяется в четыре раза. Это отличает квадратичную зависимость от линейной зависимости, где расстояние изменяется вдвое.
Принцип работы

Принцип работы квадратичной зависимости основан на принципе, что значение переменной y зависит от значения переменной x по определенному закону. В случае квадратичной зависимости, этот закон описывается квадратным уравнением y = ax^2 + bx + c, где a, b и c — это коэффициенты, определяющие форму и положение кривой. Это уравнение представляет собой параболу, которая может быть направленной вверх или вниз в зависимости от знака коэффициента a.
Принцип работы квадратичной зависимости можно легко понять, рассмотрев несколько примеров. Например, при моделировании броска предмета в воздух, высота h, на которую поднимается предмет, зависит от времени t с учетом силы тяжести и начальной скорости предмета. В данном случае зависимость является квадратичной, так как высота изменяется в зависимости от квадрата времени.
Еще одним примером квадратичной зависимости является закон Гука, который описывает связь между силой, действующей на пружину, и ее деформацией. Сила, действующая на пружину, пропорциональна квадрату ее деформации.
Квадратичная зависимость имеет широкое применение в различных областях, от физики и математики до экономики и социальных наук. Понимание принципов работы квадратичной зависимости позволяет лучше понять мир вокруг нас и применять этот знак в практических ситуациях.
Квадратичная зависимость: определение, принцип работы и примеры
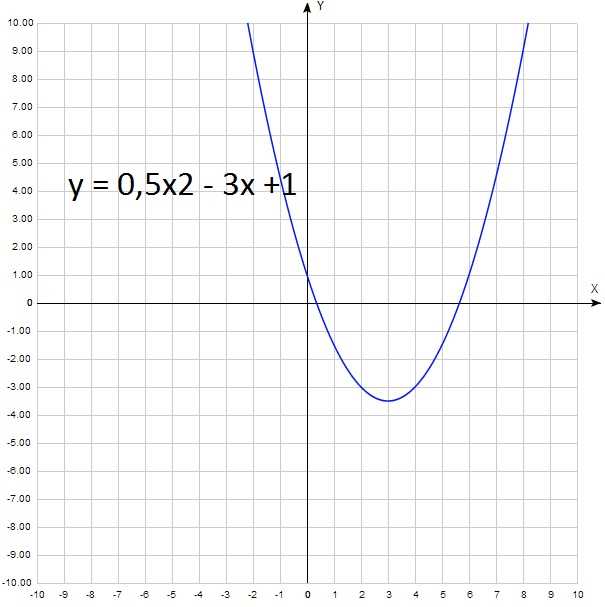
Принцип работы квадратичной зависимости основан на математической формуле y = ax^2 + bx + c, где y — зависимая переменная, x — независимая переменная, а a, b, c — коэффициенты. Зная значения коэффициентов, можно определить форму квадратичной функции: ветви параболы направлены вверх или вниз, местоположение вершины и ось симметрии.
Примеры квадратичной зависимости:
- Выброс мяча в воздух: высота, на которую поднимается мяч, зависит от времени. На первой секунде высота может быть 5 метров, на второй секунде — уже 20 метров, на третьей — 45 метров и так далее. В данном случае, время является независимой переменной, а высота — зависимой.
- Стоимость производства товара: чем больше товаров производится, тем выше затраты на производство. Если производство удваивается, то затраты увеличиваются в четыре раза. Здесь, количество произведенных товаров — независимая переменная, а затраты на производство — зависимая.