
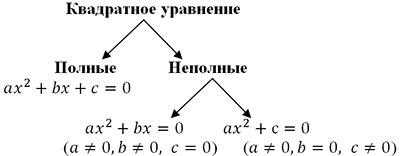
Квадратное уравнение это уравнение вида ax^2 + bx + c = 0, где a, b и c являются коэффициентами, а x — неизвестная переменная. Оно получило свое название из-за присутствия переменной второй степени. Квадратные уравнения широко используются в математике и физике для решения различных проблем. Решение квадратного уравнения дает значения переменной, при которых уравнение становится верным. Например, если у нас есть квадратное уравнение x^2 — 4 = 0, решением будет x = -2 и x = 2. Квадратные уравнения имеют множество приложений и сочетают в себе интерес и сложность.
Определение
ax2 + bx + c = 0,
где a, b и c — коэффициенты, причем коэффициент a не равен нулю. Коэффициенты могут быть целыми числами, рациональными числами, иррациональными числами или комплексными числами.
Квадратное уравнение получило свое название из-за того, что один из его членов является квадратом переменной. Графически, квадратное уравнение представляет собой параболу, которая может быть направленной вверх (если коэффициент a положительный) или вниз (если коэффициент a отрицательный).
Важно понимать, что квадратное уравнение имеет два возможных решения, которые могут быть реальными числами или комплексными числами. Это означает, что график параболы пересекает ось x в двух точках или касается ее в одной точке. Если график не пересекает ось x, то у уравнения нет решений.
Квадратные уравнения имеют широкое применение в различных областях, таких как физика, экономика, инженерия и компьютерные науки. Они позволяют решать задачи, связанные с нахождением корней, определением максимума или минимума, анализом графиков и моделированием сложных систем.
Теперь, когда вы знаете, что такое квадратное уравнение, попробуйте решить некоторые примеры и проверьте свои навыки в алгебре!
Квадратное уравнение: определение и примеры

ax2 + bx + c = 0
Здесь a, b и c – коэффициенты, причем a не равно нулю.
Основной метод решения квадратных уравнений – это формула дискриминанта:
D = b2 — 4ac
Зная значение дискриминанта, можно определить тип решений:
- Если D > 0, то квадратное уравнение имеет два различных корня;
- Если D = 0, то квадратное уравнение имеет один корень (два одинаковых корня);
- Если D < 0, то квадратное уравнение не имеет действительных корней.
Примеры квадратных уравнений:
- x2 — 5x + 6 = 0
- 2x2 + 3x — 2 = 0
- 4x2 — 9 = 0
Решение этих уравнений можно найти, применяя формулу дискриминанта и дальнейшие математические операции.





