Квадратные уравнения – это уравнения вида ax² + bx + c = 0, где a, b и c – это коэффициенты, может быть известными или неизвестными числами.
Уравнение имеет квадратный вид из-за присутствия переменной возводимой в степень 2. Решение таких уравнений позволяет нам найти значения, при которых уравнение будет выполняться.
Существуют различные методы решения квадратных уравнений, включая факторизацию, метод дополнения квадрата и использование квадратного корня. Каждый из этих методов имеет свои преимущества и применяется в зависимости от конкретной ситуации.
Изучение квадратных уравнений является важной частью алгебры и науки в целом, так как оно помогает нам понять и решить множество проблем и задач, связанных с переменными и их взаимодействием.
- Определение
- Квадратное уравнение: основное понятие и методы решения
- Какие уравнения являются квадратными?
- Методы решения квадратных уравнений
- 1. Формула дискриминанта
- 2. Факторизация
- 3. Завершение квадрата
- 4. Графический метод
- Формула дискриминанта
- Метод идеальных квадратов
- Квадратные уравнения: определение и методы решения
Определение
ax2 + bx + c = 0,
где a, b и c — это коэффициенты, и a должно быть неравным нулю.
Такое уравнение получило свое название из-за наличия переменной в квадрате. Оно содержит два решения или корня, которые могут быть как вещественными, так и комплексными числами.
Квадратные уравнения широко применяются в различных областях, таких как математика, физика, инженерия и экономика, и их решение является важным навыком.
Интересно, что уже в древности были разработаны методы решения квадратных уравнений. Бабилонский математический текст, найденный в Иране, содержит первые известные записи о решении квадратных уравнений в более чем 4000 лет до нашей эры.
Решение квадратного уравнения может быть найдено с использованием формулы, известной как «формула квадратного корня». Эта формула позволяет найти значения переменной x, которые удовлетворяют уравнению.
Зная определение и основные методы решения квадратных уравнений, вы сможете решать различные задачи, находить значения переменной и применять их в реальной жизни. Квадратные уравнения — это интересная и полезная область математики, которая позволяет нам лучше понять мир вокруг нас.
Квадратное уравнение: основное понятие и методы решения
Квадратное уравнение — это уравнение вида ax^2 + bx + c = 0, где a, b и c — коэффициенты уравнения, причем a не равно нулю. Здесь x — неизвестное значение, которое мы хотим найти.
Квадратное уравнение также может быть представлено в виде (x — x1)(x — x2) = 0, где x1 и x2 — корни уравнения, то есть значения x, которые удовлетворяют уравнению. Подстановка значений x1 и x2 в исходное уравнение должна давать нам ноль.
Решение квадратных уравнений можно осуществлять с помощью различных методов, таких как:
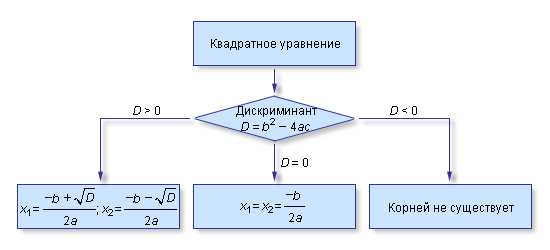
- Формула дискриминанта: Дискриминант D = b^2 — 4ac позволяет нам определить тип решений: если D > 0, то уравнение имеет два различных корня, если D = 0, то уравнение имеет один корень, а если D < 0, то уравнение не имеет решений в действительных числах.
- Метод завершения квадратного трехчлена: Этот метод заключается в приведении уравнения к виду (x + a)^2 = b, где a и b — некоторые числа. Затем мы находим корень квадратный из обеих частей уравнения и решаем полученное уравнение.
- Графический метод: Строим график функции, представленной уравнением, и находим точки пересечения графика с осью x, которые являются корнями уравнения.
Необходимо отметить, что квадратные уравнения имеют широкий спектр применений в различных науках и областях, таких как физика, экономика и инженерия. Они помогают решать задачи, связанные с движением тел, нахождением оптимальных решений, анализом систем и конструкций.
Хоть начальное изучение квадратных уравнений может показаться немного сложным, со временем вы освоите различные методы решения и научитесь использовать их для решения задач. Кроме того, непосредственное применение этих знаний в реальных ситуациях поможет вам не только в повседневной жизни, но и в развитии логического мышления и аналитических навыков.
Так что не пугайтесь, когда увидите квадратное уравнение — оно не так уж страшно, как кажется на первый взгляд. Надеюсь, эти базовые понятия и методы помогут вам стать увереннее в решении квадратных уравнений, и вы с легкостью справитесь с любыми математическими трудностями!
Какие уравнения являются квадратными?
Здравствуйте! Сегодня мы поговорим о квадратных уравнениях. Если вы интересуетесь математикой, то, скорее всего, вы уже слышали о них. Но что же это за уравнения и какие они бывают?
Квадратные уравнения — это уравнения вида ax^2 + bx + c = 0, где a, b и c — произвольные числа, причем a ≠ 0. Посмотрите на это уравнение. Не так уж сложно, верно? Кажется, что это просто мешанка букв и чисел. Но на самом деле, квадратные уравнения — это нечто большее, они имеют глубокий смысл и применяются во многих областях науки и техники.
Когда мы решаем квадратное уравнение, мы ищем значения переменной x, при которых условие уравнения становится истинным. Однако, не все уравнения могут быть решены с помощью аналитических методов. Вот почему квадратные уравнения настолько важны — они довольно универсальны и позволяют нам находить решения для широкого диапазона задач.
Так какие же уравнения могут быть квадратными? Во-первых, уравнение должно содержать квадратный член — это часть с переменной, возведенной в квадрат. Например, x^2, y^2 или z^2. Если у вас есть такой член в уравнении, то на этапе выделения нужно попытаться привести его к единственному виду, как в общей форме квадратного уравнения.
Во-вторых, уравнение должно быть линейным по каждой переменной. Это означает, что каждая переменная должна встречаться только в первой степени. Например, x, y или z. Если у вас есть переменные с более высокими степенями или уравнение явно нелинейно, то это уже не квадратное уравнение.
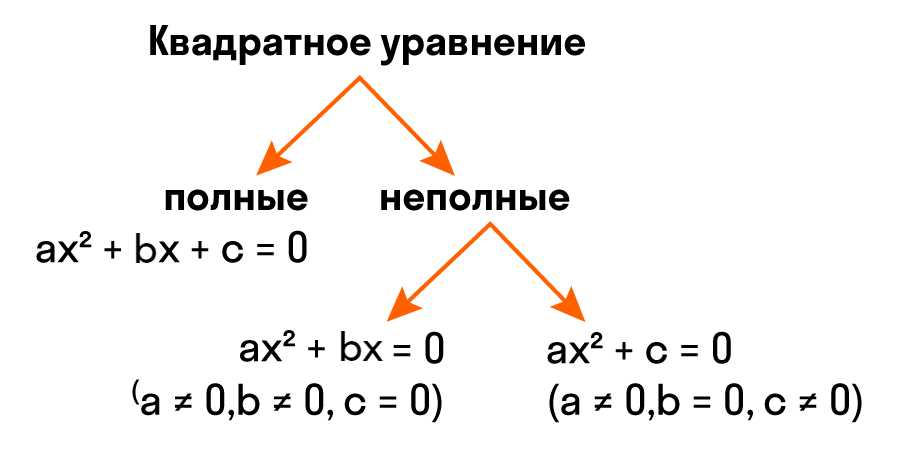
Кроме того, уравнение должно быть полным, это означает, что все коэффициенты — a, b и c должны быть определены. Если один или несколько из них отсутствуют или равны нулю, то это также уже не квадратное уравнение.
Таким образом, чтобы узнать, является ли уравнение квадратным, нужно проверить, выполняет ли оно все указанные выше условия: наличие квадратного члена, линейность по каждой переменной и полноту коэффициентов.
Надеюсь, что я смог разъяснить, какие уравнения являются квадратными и почему они важны. Теперь вы знаете, что такое квадратные уравнения и сможете узнавать и решать их, когда они вам встретятся. Удачи в изучении математики!
Методы решения квадратных уравнений

1. Формула дискриминанта
Один из наиболее распространенных и полезных методов решения квадратных уравнений — использование формулы дискриминанта. Дискриминант определяется как D = b^2 — 4ac, и его значение позволяет определить количество и тип корней уравнения.
- Если D > 0, то уравнение имеет два разных вещественных корня.
- Если D = 0, то уравнение имеет один вещественный корень.
- Если D < 0, то уравнение имеет два комплексных корня.
Если дискриминант положителен, можно использовать формулу для нахождения корней уравнения: x1 = (-b + √D) / (2a) и x2 = (-b — √D) / (2a). Если дискриминант равен нулю, уравнение имеет единственный корень, который может быть найден по формуле x = -b / (2a). В случае отрицательного дискриминанта, уравнение имеет два комплексных корня и их можно найти, используя формулу x1 = (-b + i√|D|) / (2a) и x2 = (-b — i√|D|) / (2a).
2. Факторизация
Другой метод решения квадратных уравнений — это факторизация. Он основывается на том, что квадратное уравнение можно представить в виде произведения двух множителей. Чтобы применить этот метод, нужно найти такие числа, которые при умножении дают свободный член c и при сложении дают коэффициент b. Затем уравнение можно записать в виде (ax + m)(ax + n) = 0, где m и n — найденные числа. Затем можно найти значения x, приравняв каждый множитель к нулю и решив полученные уравнения.
3. Завершение квадрата
Метод завершения квадрата основан на преобразовании квадратного уравнения до вида (x + p)^2 = q, где p и q — известные числа. Это упрощает решение уравнения, так как теперь можно найти значение x, равное квадратному корню числа q, измененному знаком p.
Для завершения квадрата можно использовать следующие шаги:
- Перепишите уравнение в виде ax^2 + bx = -c.
- Добавьте и вычтите к левой стороне уравнения число (b/2a)^2, чтобы завершить квадрат.
- Упростите уравнение до вида (x + b/2a)^2 = (b^2 — 4ac) / (4a^2).
- Найдите квадратный корень с обеих сторон уравнения и решите полученное уравнение относительно x.
4. Графический метод

Графический метод решения квадратных уравнений основан на построении графика функции y = ax^2 + bx + c и определении точек его пересечения с осью x. Если на графике есть точки пересечения, то их координаты будут являться корнями уравнения.
Чтобы найти корни графически, нужно построить график функции и найти точки пересечения с осью x. В этом случае значение x будет соответствовать корням уравнения.
В завершение, хочется отметить, что каждый из этих методов имеет свои преимущества и может быть удобным в разных ситуациях. Важно уметь применять их грамотно и знать, какой метод лучше всего подходит для конкретной задачи. Практикуйтесь в решении квадратных уравнений разными способами, и вы сможете легко и быстро решать любые задачи этого типа. Удачи!
Формула дискриминанта
Формула дискриминанта используется для определения числа корней квадратного уравнения. Квадратное уравнение имеет вид ax^2 + bx + c = 0, где a, b и c — это числа, называемые коэффициентами. Важной частью этого уравнения является то, что a не может быть равно нулю, потому что это превратило бы уравнение в линейное, а не квадратное.
Теперь давай рассмотрим саму формулу дискриминанта. Она вычисляется по формуле: D = b^2 — 4ac. В этой формуле b и c — это коэффициенты из квадратного уравнения, а D — это сам дискриминант. Прошу заметить, что важно понимать, что формула дискриминанта применяется только к квадратным уравнениям.
Теперь подумай, зачем нам нужен дискриминант? Он помогает нам определить количество корней у квадратного уравнения. Исходя из значений, которые может принимать дискриминант, мы можем сказать следующее:
- Если D > 0, то уравнение имеет два различных корня.
- Если D = 0, то уравнение имеет один корень, который называется «корнем кратности 2».
- Если D < 0, то уравнение не имеет действительных корней. Однако, уравнение может иметь комплексные корни.
Примеры всегда помогают нам лучше понять. Рассмотрим уравнение x^2 — 5x + 6 = 0. Сначала мы можем найти дискриминант, применив формулу: D = (-5)^2 — 4(1)(6) = 25 — 24 = 1. Так как D > 0, это означает, что у уравнения есть два действительных корня.
Теперь ты знаком с формулой дискриминанта и с тем, как ее использовать для определения количества корней квадратного уравнения. Не бойся чисел, букв и знаков равенства — они приведут тебя к интересным и вдохновляющим открытиям. Уверен, что со временем, ты будешь решать квадратные уравнения, как настоящий математический гений! Вперед к новым знаниям и невероятному успеху!
Метод идеальных квадратов
Когда мы сталкиваемся с квадратным уравнением, первое, что приходит в голову, это использование формулы дискриминанта или метода дополнения квадрата. Однако, существует еще один довольно интересный и эффективный метод решения квадратных уравнений, известный как метод идеальных квадратов.
В методе идеальных квадратов мы ищем ближайший целочисленный корень и затем складываем или вычитаем определенное число, чтобы получить другой целочисленный корень. Давайте рассмотрим пример для большей ясности.
Предположим, у нас есть квадратное уравнение: x^2 + 10x + 25 = 0
Для начала обратим внимание на выражение 10x. Здесь мы видим, что при множении x на 5 и 5, мы получим число 25, а затем при сложении этих двух чисел мы получим число 10x.
Теперь давайте перепишем уравнение с каким-то изменением: x^2 + 10x + 25 — 25 = 0
Отнимая число 25, мы на самом деле не меняем смысл уравнения, так как это эквивалентно вычитанию нуля. Теперь разделим это выражение на два квадрата: x^2 + 10x + (5^2 — 5^2) = 0
После этого мы получаем уравнение x^2 + 10x + 5^2 — 5^2 = 0
А это уже можно переписать в следующем виде: (x + 5)^2 — 5^2 = 0
Теперь, давайте продолжим работу с данным выражением. Здесь у нас есть разность двух квадратов, но мы можем представить ее как произведение суммы и разности: ((x+5)-5)((x+5)+5) = 0
Раскроем скобки: (x+5-5)(x+5+5) = 0
Упростим получившееся выражение и получим: (x)(x+10) = 0
Теперь мы можем видеть, что один из корней равен нулю, а второй корень равен -10. Итак, решение нашего исходного квадратного уравнения: x = 0 или x = -10
Как видите, метод идеальных квадратов дает нам возможность решить квадратное уравнение, используя простые математические операции подходящего вида. Этот метод особенно полезен, когда у нас есть целочисленные корни и позволяет нам более быстро и эффективно найти решение.
Квадратные уравнения: определение и методы решения
ax^2 + bx + c = 0, где a, b и c — заданные числа, причем a ≠ 0.
Квадратное уравнение может иметь один, два или ни одного решения в зависимости от значения дискриминанта D, который определяется по формуле: D = b^2 — 4ac.
Если D > 0, то квадратное уравнение имеет два различных вещественных корня.
Если D = 0, то квадратное уравнение имеет один вещественный корень.
Если D < 0, то квадратное уравнение не имеет вещественных корней.
Найдем корни квадратного уравнения:
- Если квадратное уравнение имеет два корня, то они находятся по формулам:
x1 = (-b + √D) / (2a),
x2 = (-b — √D) / (2a).
- Если квадратное уравнение имеет один корень, то он находится по формуле:
x = -b / (2a).
В таблице ниже приведены возможные случаи значения дискриминанта и количества корней квадратного уравнения:
| Значение D | Количество корней |
|---|---|
| D > 0 | 2 |
| D = 0 | 1 |
| D < 0 | 0 |