
Определение квадратного корня в 8 классе
Квадратный корень – это операция, обратная возведению в квадрат. Он позволяет найти число, которое при возведении в квадрат даст нам исходное число. Например, квадратный корень из числа 9 равен 3, так как 3 умноженное на 3 дает 9.
Когда мы записываем квадратный корень, мы используем символ √. Например, корень из числа 9 записывается как √9 = 3. Также можно записать в виде √9 = ±3. Это означает, что есть два числа — положительное и отрицательное — которые при возведении в квадрат дают 9.
Теперь, когда мы знаем, что такое квадратный корень, давайте посмотрим, как мы можем вычислять его и использовать в наших решениях задач. Возможно, вам уже приходилось сталкиваться с этим в прошлом, но давайте обновим ваши знания и углубим их.
Таким образом, определение квадратного корня в 8 классе – это операция нахождения числа, которое при возведении в квадрат даст нам исходное число. Мы используем символ √ для обозначения квадратного корня и можем вычислять его с помощью таблицы квадратов или других методов. Квадратный корень часто встречается в математических задачах, поэтому хорошо его понимать и знать правила его вычисления. Будьте уверены в своих знаниях и не стесняйтесь применять их в своей работе!
Понятие квадратного корня

Здравствуйте! Сегодня мы поговорим о квадратном корне. Возможно, вы уже слышали об этом математическом понятии, но давайте вместе углубимся в его суть.
Квадратный корень — это математическая операция, которая позволяет найти число, умноженное на себя, равное заданному числу. Например, если мы возьмем квадратный корень из 25, то получим число 5, потому что 5 * 5 = 25. В данном случае, число 5 является квадратным корнем числа 25. Обозначается квадратный корень символом √.
Квадратный корень может быть как положительным, так и отрицательным. Однако, по соглашению, когда мы говорим о квадратном корне, мы подразумеваем только положительное число. Например, когда мы говорим о квадратном корне из 25, мы имеем в виду число 5, а не -5.
Для вычисления квадратного корня мы используем определенные правила. Давайте рассмотрим некоторые из них:
- Правило 1: Квадратный корень из произведения равен корню из каждого множителя. Например, √(a * b) = √a * √b.
- Правило 2: Корень из суммы или разности нельзя сократить до суммы или разности корней. Например, √(a + b) ≠ √a + √b и √(a — b) ≠ √a — √b.
- Правило 3: Квадратный корень из квадрата числа равен самому числу. Например, √(a^2) = a.
- Правило 4: Квадратный корень из квадрата корня равен самому корню. Например, √(√a^2) = √a.
Важно помнить, что квадратный корень — это не только абстрактное математическое понятие, но и полезный инструмент в повседневной жизни. Например, когда мы хотим найти длину стороны квадрата с заданной площадью, мы используем квадратный корень. Или когда мы хотим вычислить среднее арифметическое из нескольких чисел, мы также можем применить квадратный корень.
Так что не стесняйтесь использовать квадратный корень в своих математических расчетах и повседневной жизни. Он поможет вам найти решения и раскрыть новые возможности!
Как вычислять квадратный корень в 8 классе
Учимся вычислять квадратный корень – это приключение, которое открывает перед нами двери в мир математики. Запомните, что квадратный корень числа а это такое число b, что b*b=a. Например, корень из 9 равен 3, потому что 3*3=9. Звучит просто, верно?
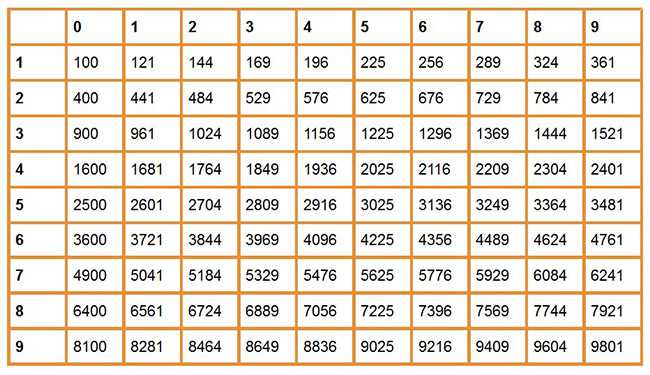
Первый шаг в вычислении квадратного корня – это разложение числа на множители. Вы можете вспомнить правило разложения квадратов на множители или воспользоваться таблицей квадратов чисел до 100. Не пугайтесь, если таблица кажется огромной, потому что вы с каждым днем будете заполнять ее все больше и больше!
Например, если вы хотите найти квадратный корень числа 16, мы можем разложить 16 на множители: 4 * 4 = 16. Это означает, что корень из 16 равен 4.
Когда мы разложили число на множители, мы можем сократить корни с одинаковыми множителями. Например, корень из 36 равен 6, потому что 6 * 6 = 36. Мы можем также записать корень из 36 как 2 * 3 * 3, и сократить две тройки. Получается, корень из 36 равен 6.
Конечно, это всего лишь простейшие примеры, и в реальной жизни нам может потребоваться вычислить корень из числа, которое не является точным квадратом. В таком случае мы можем использовать приближенные методы, такие как метод двух ближайших квадратов или метод деления отрезка пополам.
Не забывайте, что решение примеров с квадратными корнями требует тренировки и практики. Чем больше упражнений вы выполните, тем легче и быстрее вы будете находить квадратные корни. И помните, что с помощью квадратных корней вы сможете решать разнообразные задачки в математике и реальной жизни. Знания – это сила, которая всегда пригодится вам!
Итак, друзья, что мы узнали сегодня? Мы обсудили, как вычислять квадратный корень, разложение числа на множители, сокращение корней и приближенные методы. Не забывайте практиковаться и задавать себе вопросы, чтобы углубить свое понимание темы. Уверен, что вы справитесь с этим! Удачи вам в изучении математики!
Правила вычисления чисел с целыми корнями
Дорогой читатель!
Сегодня я хочу рассказать тебе о правилах вычисления чисел с целыми корнями. Мы уже знаем, что квадратный корень числа можно найти, если число представлено в виде произведения двух одинаковых множителей. Но что делать, если число не имеет целого квадратного корня? Не беспокойся, у меня есть для тебя несколько интересных советов!
Первое правило: никогда не пренебрегай разложением числа на простые множители. Если ты не знаешь, как разложить число на множители, спроси у своего учителя или воспользуйся справочником. Когда ты разложишь число на простые множители, посмотри, есть ли среди них повторяющиеся. Если да, значит, у тебя есть целый квадратный корень!
Второе правило: сопоставление долей разложенного числа. Если у тебя есть квадратный корень из некоторых множителей разложенного числа и они умножены на другие множители, то можно вынести квадратный корень за знак радикала и умножить его на корень оставшихся множителей. Таким образом, ты сможешь упростить выражение и получить более точный результат.
Третье правило: произведение корней. Если у тебя есть несколько чисел с целыми корнями, то результатом их умножения будет корень из произведения этих чисел. Например, корень из числа 4 умноженный на корень из числа 9 будет равен корню из 36.
Четвертое правило: умножение числа на само себя. Чтобы получить корень числа, умножь его само на себя. Например, корень числа 25 равен 5, так как 5 умноженное на 5 даёт 25.
Пятая совет: не забывай проверять свои результаты. Не стесняйся использовать калькулятор, учебник или интернет, чтобы убедиться в правильности вычислений.
Теперь ты знаешь несколько полезных правил, которые помогут тебе вычислять числа с целыми корнями. Помни, что практика делает мастера, поэтому не бойся практиковаться и задавать вопросы, если что-то непонятно. Уверен, что ты справишься!
Правила вычисления чисел с нецелыми корнями

Первым правилом является упрощение корня. Если под корнем находится полный квадрат, то корень может быть упрощен. Например, квадратный корень из 9 равен 3, так как 3 × 3 = 9. Это правило также применимо к другим полным квадратам, например, квадратному корню из 16, который равен 4.
Вторым правилом является использование свойства мультипликативности. Если у нас есть произведение под корнем, то мы можем разделить это произведение на множители и выделить каждый множитель под отдельный корень. Например, квадратный корень из произведения a × b равен квадратному корню из a, умноженному на квадратный корень из b.
Третьим правилом является работа с отрицательными числами. Нецелые корни могут иметь отрицательное значение. Например, квадратный корень из -9 равен корню из 9, домноженному на комплексное число i. Комплексное число i, также известное как мнимая единица, определено как квадратный корень из -1.
И, наконец, четвертое правило связано с работой с дробями. Если у нас есть дробное число под корнем, то мы можем разложить это число на две части: числитель и знаменатель. Затем мы вычисляем корни числителя и знаменателя отдельно и делим результаты друг на друга. Например, квадратный корень из дроби 16/25 равен корню из 16, разделенному на корень из 25. Таким образом, это правило позволяет нам вычислить корень дробного числа.
Итак, эти четыре правила помогают нам вычислить числа с нецелыми корнями. Используя их, мы можем упростить корни, разбивать произведения, работать с отрицательными числами и вычислять дробные корни. Зная эти правила, вы сможете успешно решать задачи, связанные с квадратными корнями и другими нецелыми корнями. Удачи вам!
Квадратный корень 8 класс: понятие и правила вычисления
Для вычисления квадратного корня используются следующие правила:
- Если число положительное, то его квадратный корень существует и является действительным числом.
- Если число отрицательное, то его квадратный корень не существует в множестве действительных чисел. В этом случае используется понятие комплексных чисел.
- Если число равно нулю, то его квадратный корень также равен нулю.
Для вычисления квадратного корня из положительного числа можно воспользоваться следующими правилами:
- Если число является точным квадратом другого числа (например, 4, 9, 16 и т.д.), то его квадратный корень можно найти без использования калькулятора. Для этого нужно найти число, при возведении в квадрат которого получается заданное число.
- Если число не является точным квадратом, то его квадратный корень можно приближенно найти с помощью калькулятора или специальных таблиц.
Квадратный корень широко используется в различных областях науки и техники, включая физику, инженерию и программирование.




