Лекальные кривые: все, что нужно знать и как их использовать

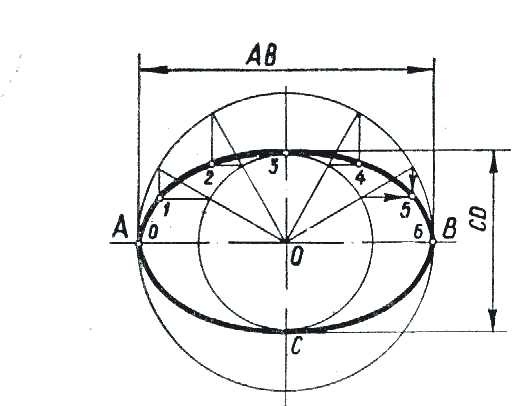
Лекальные кривые: подробное описание и использование

Что такое лекальные кривые?

В простых словах, лекальные кривые — это математические модели, описывающие формы, которые могут быть созданы путем комбинирования базовых геометрических элементов, таких как точки, прямые и кривые линии. Лекальные кривые обладают особыми свойствами, которые позволяют им адаптироваться к различным требованиям проектирования и моделирования.

Одно из основных преимуществ лекальных кривых заключается в их гибкости и адаптивности. Их форма может изменяться, приспосабливаясь к параметрам, заданным пользователем, и обладать определенными свойствами, такими как гладкость, симметрия или согласованность с оригинальным изображением.

Применение лекальных кривых

• Индустрия развлечений и фильмов: лекальные кривые широко используются в создании анимационных персонажей, моделировании сцен и создании спецэффектов. Благодаря гибкости и адаптивности, лекальные кривые позволяют создавать плавные и реалистичные движения.
• Дизайн и искусство: лекальные кривые могут быть использованы для создания интересных и уникальных форм и моделей, будь то ювелирные изделия, мебель или архитектурные элементы. Они предоставляют дизайнерам и художникам бесконечные возможности для творчества.
• Инженерия и проектирование: лекальные кривые являются важным инструментом в области инженерного моделирования и проектирования. Они могут быть использованы для создания сложных форм и моделей, а также для анализа и оптимизации конструкций.

Лекальные кривые — это мощный инструмент для создания и моделирования форм и объектов в различных областях. Они позволяют проектировать и создавать что-то новое и уникальное, реализуя свою креативность и творческие идеи. Кроме того, они способствуют более эффективному и обоснованному подходу к инженерным проектам, что способствует сокращению времени и затрат.

Так что, если вы всегда хотели попробовать что-то новое и увлекательное, возможно, лекальные кривые — это то, что вам нужно. Дайте волю своей творческой энергии и начните экспериментировать с этим удивительным видом кривых. Кто знает, может быть вы откроете в себе новые возможности и станете настоящим мастером лекальных кривых!

Определение

Одной из ключевых особенностей лекальных кривых является то, что они могут иметь разные кривизны и точки перегиба. Кривизна определяет скорость изменения направления кривой в каждой ее точке, а точка перегиба — это точка на кривой, в которой меняется направление кривизны. Эти свойства делают лекальные кривые полезными в различных областях, таких как математика, физика, инженерия и многое другое.

Лекальные кривые имеют множество практических применений. Например, они широко используются в графике и компьютерной графике для создания красивых и реалистических изображений. Они также применяются в физике для моделирования движения объектов и прогнозирования их поведения. Кроме того, они используются в инженерии для проектирования сложных структур, таких как мосты и здания. В медицине они используются для анализа и визуализации данных, полученных из различных исследований и тестов.

Использование лекальных кривых требует знания и понимания их математических и геометрических свойств. Однако, современные программы и инструменты позволяют нам создавать и манипулировать лекальными кривыми без необходимости в глубоких знаниях математики. Например, с помощью графических редакторов и компьютерных программ можно создавать и изменять формы лекальных кривых с помощью простых инструментов и операций.

Так что, давайте погрузимся в мир лекальных кривых и узнаем больше об их формах, свойствах и использовании!

Примеры

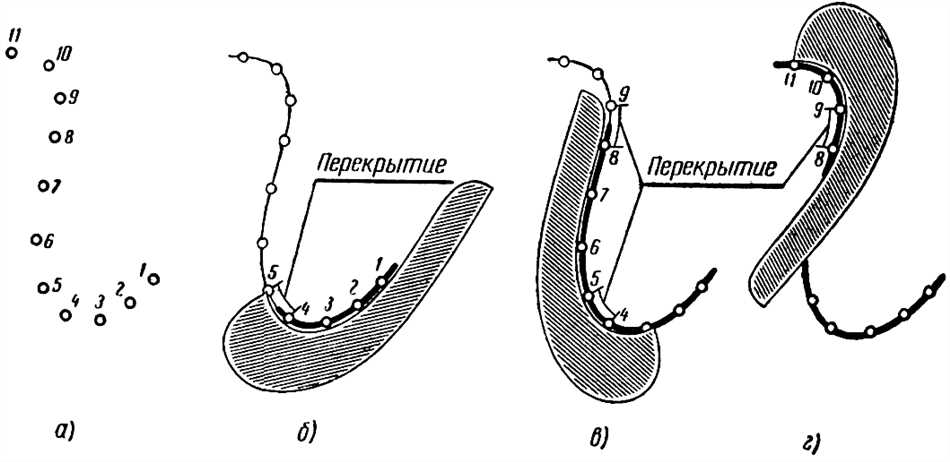
Теперь, когда мы обсудили основы и принципы использования лекальных кривых, давайте рассмотрим несколько примеров, чтобы лучше понять их практическое применение.

1. Создание анимации

Лекальные кривые могут быть использованы для создания плавных анимаций. Например, вы можете использовать кривую, чтобы задать позицию объекта на экране в разных точках времени. Это позволит объекту плавно перемещаться с одного места на другое, создавая эффект анимации.

2. Ретуширование фотографий

Лекальные кривые также широко используются при редактировании фотографий. Они позволяют корректировать цвета, контрастность и яркость изображения, достигая большей точности и контроля. С помощью кривых можно легко устранить некоторые дефекты, например, уравнять цвета фотографии или сделать ее более насыщенной и выразительной.

3. Создание графических эффектов

Если вы хотите добавить визуальных эффектов к своему дизайну, лекальные кривые могут стать мощным инструментом. Их можно применять для создания различных эффектов, таких как градиенты, выпуклости, каркасы и многое другое. Можете представить, как интересно будет использовать эти возможности для создания оригинальных и запоминающихся графических элементов.

4. Формирование математических моделей

Лекальные кривые также находят применение в математическом моделировании. Они могут использоваться для описания и аппроксимации сложных форм и контуров. Например, в аэродинамике и автомобильной промышленности лекальные кривые используются для создания прецизионных моделей крыла или кузова автомобиля.

Все эти примеры лишь небольшая часть того, что можно сделать с помощью лекальных кривых. Важно помнить, что их применение не ограничено только этими сферами. Начните экспериментировать с этим мощным инструментом, и вы увидите, что возможности его использования бесконечны.

Применение лекальных кривых

Лекальные кривые нашли применение во множестве областей, от графики и дизайна до компьютерного моделирования и анимации. Они предоставляют возможность создавать сложные и органические формы, которые представляют собой плавные переходы между точками.

Одним из основных применений лекальных кривых является создание графических изображений и дизайна. Они позволяют проектировать объекты с плавными линиями и кривыми, что придает им эстетичность и привлекательность. Кроме того, лекальные кривые могут использоваться для создания теней, эффектов освещения и других графических эффектов, которые придают изображению реалистичность и объемность.

Лекальные кривые также широко используются в компьютерной графике и анимации. Благодаря своей гибкости и возможности создавать плавные движения, они позволяют аниматорам создавать реалистичные анимационные персонажи и объекты. Они также используются для создания специальных эффектов, таких как взрывы, жидкость, огонь и многое другое.

Лекальные кривые имеют применение и в компьютерном моделировании и виртуальной реальности. Они позволяют создавать 3D-модели объектов и окружающей среды, при этом обеспечивая плавные и органичные формы. Это не только облегчает процесс создания моделей, но и делает их более реалистичными и приятными для восприятия.

Кроме того, лекальные кривые находят применение в разработке игр и визуализации данных. Они позволяют создавать сложные трехмерные объекты и сцены, а также анимировать их с высокой степенью детализации и реализма. Таким образом, они делают игровой процесс более интересным и привлекательным для игроков, а также обеспечивают более наглядную и понятную отображение данных.

В итоге, применение лекальных кривых является неотъемлемой частью современной графики, дизайна и компьютерных технологий. Они позволяют создавать сложные и органические формы, которые придают изображениям и объектам эстетичность, реализм и привлекательность. Независимо от области, в которой они используются, лекальные кривые являются мощным инструментом для воплощения творческих идей и визуализации сложных концепций.

Графика и дизайн

Одним из важных аспектов графики и дизайна является умение создавать привлекательные и эффективные визуализации. Это может быть отдельные иллюстрации, рекламные плакаты, логотипы или целые композиции, такие как веб-страницы или дизайн интерфейсов.

Дизайнеры графики и дизайна должны уметь применять различные техники и инструменты, чтобы создать эффективные и привлекательные визуализации. Они могут использовать цвет, форму, текстуру и пропорции, чтобы вызвать определенные эмоции или передать определенную информацию. Использование типографии, композиции и пространства также является важной частью процесса дизайна.

Графика и дизайн также имеют большое значение в сфере маркетинга и рекламы. Привлекательная визуализация может привлечь внимание потенциальных клиентов и вызвать у них интерес к продукту или услуге. Она также может помочь установить эмоциональное соединение с целевой аудиторией и создать уникальный образ бренда.

В современном мире графика и дизайн стали еще более доступными благодаря развитию технологий и появлению специализированного программного обеспечения. Сейчас каждый может стать дизайнером и создавать собственные уникальные проекты. Это открывает огромные возможности для самовыражения и развития творческого потенциала.

Медицина

Здравствуйте, уважаемый читатель!

Сегодня я хотел бы поговорить с вами о медицине — науке, которая помогает нам заботиться о нашем здоровье и лечить различные заболевания. Медицина — это не только профессия врачей, но и часть нашей повседневной жизни.

Медицина существует уже множество веков. Изначально она была основана на накопленных знаниях и опыте, передаваемых из поколения в поколение. Сегодня медицина стала наукой, базирующейся на современных исследованиях и технологиях. Каждый день медицинские ученые работают над разработкой новых лекарств и методов лечения.

Медицина имеет разные направления и специализации. Например, общая медицина, педиатрия, гинекология, хирургия, стоматология и многие другие. В каждой области медицины есть свои эксперты, специализирующиеся именно в этих областях. Это позволяет им быть владельцами глубоких знаний и навыков в своих областях, что способствует успешному лечению пациентов.

Одним из ключевых аспектов медицины является профилактика заболеваний. Знакомы ли вы с пословицей «Предупреждение — лучшее лекарство»? Это очень важное утверждение. Регулярные медицинские осмотры, прививки, здоровый образ жизни — все это помогает предотвратить множество заболеваний и сохранить наше здоровье. Какая из этих мер вы принимаете на свой счет?

Благодаря медицине мы имеем доступ к лечению различных заболеваний. Что бы нам делали без врачей? Они помогают нам восстановиться после травм, вылечить различные инфекции, справиться с хроническими заболеваниями и даже спасают жизни. Они действительно делают благородное дело, помогая нам жить более здоровой и счастливой жизнью.

Каждый из нас хотя бы раз обращался к врачу. А какие чувства у вас вызывает это посещение? Иногда мы боимся получить неприятные новости или боимся процедур, которые назначит врач. Но не стоит бояться — врачи делают все возможное, чтобы помочь нам и обеспечить наше благополучие.

Медицина постоянно развивается и совершенствуется. Как вы думаете, какие изменения будут происходить в медицине в будущем? Возможно, роботы будут выполнять хирургические операции, или мы сможем лечить заболевания без использования лекарств. Будущее медицины выглядит очень интересным и захватывающим.

Здоровье — наше самое ценное достояние, и медицина играет важную роль в его поддержании. Помните необходимость регулярных медицинских осмотров и следуйте советам врачей. Забудьте о страхе и обратитесь к врачу, если есть какие-то проблемы со здоровьем.

Желаю вам крепкого здоровья и надеюсь, что этот текст расширил ваше понимание важности медицины в нашей жизни!

Криптография: защита информации в цифровом мире

Криптография используется практически повсеместно в нашей жизни. Вы наверняка уже сталкивались с ней, даже не задумываясь об этом. Например, когда вы делаете покупки в интернете, ваши данные (номер карты, адрес доставки) шифруются с помощью криптографических алгоритмов, чтобы защитить их от несанкционированного доступа. Вот и практическое применение криптографии! Другой пример — это шифрование переписки по электронной почте или мессенджеру, чтобы никто не смог прочитать ваши сообщения, кроме адресата.

Многое, многое можно сказать про криптографию, но одно из самых удивительных ее свойств — это то, что благодаря криптографии мы можем доверять друг другу даже в цифровом мире, где каждая цифра или буква важна. К примеру, при регистрации на сайте мы вводим пароль, который хранится в зашифрованном виде. А когда мы вводим пароль для входа, сайт дешифрует его и сравнивает с тем, что хранится в базе данных. И если пароли совпадают, то сайт позволяет нам войти.

Но давайте подробнее поговорим о самом интересном аспекте криптографии — лекальных кривых. Они используются для создания шифров и электронных подписей, но что они такое и зачем нужны? Лекальные кривые — это математические объекты, которые могут использоваться для шифрования данных и проверки подлинности.

Но почему именно лекальные кривые? Ответ прост, они обладают несколькими важными свойствами, которые делают их очень полезными для криптографии. Во-первых, они позволяют сгенерировать ключи, которые очень сложно подобрать или взломать. Это значит, что вашу информацию будет очень сложно расшифровать без ключа. Во-вторых, лекальные кривые обладают свойством неравномерности, благодаря которому можно создать электронную подпись, которую нам невозможно подделать. В-третьих, лекальные кривые достаточно легкие и не требуют больших вычислительных ресурсов.

Использование лекальных кривых в криптографии может предоставить нам сильную защиту и обеспечить надежность в цифровом мире. Это важно, потому что защита нашей информации — это наша ответственность. Мы не можем позволить себе рисковать нашей конфиденциальностью и безопасностью.

Надеюсь, теперь вы понимаете, насколько важна криптография в нашей повседневной жизни. Будьте внимательны и осознанными в использовании криптографических методов, чтобы ваша информация всегда была в безопасности!

Алгоритмы построения лекальных кривых

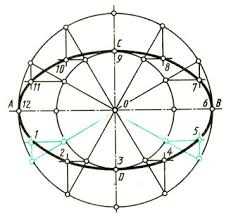
Существует несколько всем известных алгоритмов, используемых для построения лекальных кривых:

1. Алгоритм Безье

Этот алгоритм широко используется в графическом дизайне и компьютерной графике. Он основан на использовании контрольных точек, задающих форму кривой. Контрольные точки управляют положением и формой кривой, позволяя создавать плавные переходы между точками.

Алгоритм Безье может быть использован для построения как двухмерных, так и трехмерных кривых. Он отличается простотой и интуитивной понятностью, что позволяет его успешное применение в различных сферах.

2. Алгоритм Б-сплайнов

Алгоритм Б-сплайнов является более сложным и гибким по сравнению с алгоритмом Безье. Он позволяет создавать более сложные кривые с использованием промежуточных точек контроля. Б-сплайны широко используются в компьютерной графике и анимации, а также в проектировании и моделировании.

Основным преимуществом Б-сплайнов является их способность представлять сложные формы с использованием небольшого количества точек контроля. Это делает их идеальным инструментом для создания плавных и естественных кривых.

3. Алгоритм на основе физического моделирования

Этот алгоритм основан на имитации физических законов и принципов, используя математические модели. Он позволяет создавать кривые с учетом физических свойств, таких как гравитация, трение и упругость.

Основная идея этого метода заключается в том, чтобы моделировать движение частицы или объекта и проследить его траекторию. Алгоритм рассчитывает позиции частицы на каждом шаге, и затем строит кривую, проходящую через эти позиции.

Хотя это только некоторые из алгоритмов, используемых для построения лекальных кривых, каждый из них имеет свои особенности и применяется в различных областях. Выбор конкретного алгоритма зависит от конкретного проекта и требуемых свойств кривой.

Так какой алгоритм построения локальной кривой вам больше нравится?

Лекальные кривые: подробное описание и использование

Лекальные кривые применяются в различных областях, таких как физика, математика, экономика и другие. Они позволяют анализировать взаимосвязь между переменными и исследовать различные зависимости.

Описание лекальной кривой:

• Лекальная кривая представляет собой график, на котором по одной оси откладываются значения одной переменной, а по другой оси – значения другой переменной.
• На графике лекальной кривой точки, соответствующие различным значениям переменных, соединяются линиями или кривыми.
• Форма и характер лекальной кривой определяются свойствами и взаимосвязями между переменными.
• Лекальные кривые могут быть как прямолинейными, так и изогнутыми, в зависимости от свойств системы и ее компонентов.

Использование лекальных кривых:

1. Построение лекальных кривых позволяет визуально представить зависимости между переменными и анализировать эти зависимости.
2. Лекальные кривые используются для прогнозирования и моделирования различных систем.
3. Они помогают выявить закономерности и тенденции в данных, что позволяет принимать обоснованные решения.
4. Лекальные кривые также используются для оптимизации процессов в различных областях, например, в экономике и производстве.

Пример применения лекальных кривых:

Предположим, у нас есть данные о зависимости объема продаж от цены товара. Мы можем построить лекальную кривую, на которой по горизонтальной оси будет отложена цена товара, а по вертикальной оси – объем продаж. Таким образом, мы сможем определить оптимальную цену товара, при которой объем продаж будет максимальным.