В геометрии существует множество терминов и понятий, которые часто могут показаться сложными и непонятными. Один из таких терминов — лемма. Что это такое и как его можно объяснить простыми словами?
Лемма в геометрии — это вспомогательное утверждение или вспомогательное предложение, которое используется для доказательства некоторой основной теоремы. Она не является самостоятельной теоремой, но играет важную роль в построении доказательства.
Для лучшего понимания можно представить лемму как ключ к запертой двери. Она помогает разблокировать основную теорему, раскрывая ее смысл и доказательство. Без леммы, доказательство может быть сложным, неочевидным или даже невозможным.
Таким образом, лемма — это важный инструмент для геометров, который помогает им строить логически связанные и убедительные доказательства геометрических теорем.
- Что такое лемма в геометрии?
- Зачем нужны леммы в геометрии?
- Упрощение доказательств
- 1. Применение известных лемм и теорем
- 2. Использование аналогий
- 3. Разбиение задачи на более мелкие части
- 4. Использование геометрических построений и изображений
- 5. Использование аналитической геометрии
- Построение новых теорем
- Углубление понимания геометрических концепций
- Построение основных понятий
- Углы и их свойства
- Построение сложных фигур
- Заключение
- Примеры лемм в геометрии
- Лемма о сегменте
- Лемма о угле в окружности
- Лемма об антисимедиане
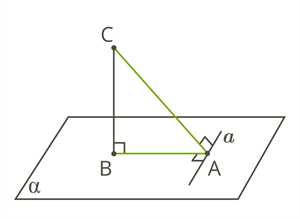
- Лемма о трех перпендикулярах
- Лемма о прямоугольнике
- Пример:
Что такое лемма в геометрии?
В геометрии лемма может быть доказана различными методами, такими как метод от противного, индукция, принцип математической индукции, метод от примера или противопримера и так далее. Главная цель леммы — помочь человеку в понимании основной теоремы и помочь решить сложную геометрическую задачу.
Особенность лемм в геометрии заключается в том, что они формулируются простым и понятным языком, чтобы каждый мог понять их смысл. Например, лемма может говорить о свойствах параллелограмма или треугольника, о соотношениях сторон и углов, о существовании основных линий и плоскостей.
При решении геометрических задач, лемма может быть полезна для построения доказательств или поиска решения. Она может помочь понять основные идеи и принципы задачи, а также предложить подход к её решению. В конечном счете, лемма способствует более глубокому пониманию геометрии и развитию аккуратности в решении задач.
Зачем нужны леммы в геометрии?
Лемма — это простое и понятное утверждение или вспомогательное предложение, которое служит основой для доказательства более сложной теоремы. В геометрии леммы играют важную роль, поскольку они помогают нам понять и объяснить различные свойства и закономерности объектов. Они являются шагом к пониманию истинной сути геометрических фактов.
Представьте, что вы стоите перед сложной задачей по доказательству теоремы. Начать сразу с доказательства сложной теоремы может быть сложно и запутанно. И вот здесь в игру вступают леммы! Они предоставляют нам промежуточные результаты и идеи, которые помогают разбить задачу на более простые и понятные части. Используя леммы, можно постепенно приблизиться к итоговому решению.
Леммы также помогают упростить доказательства и сделать их более ясными и доступными для понимания. Они позволяют нам разделить доказательство на логические шаги, каждый из которых подтверждает определенный аспект или утверждение. Это помогает нам легче следовать линии рассуждений и сделать убедительное заключение.
Кроме того, леммы способствуют развитию и укреплению наших умственных способностей. При их использовании мы учимся логическому мышлению, анализировать информацию и строить аргументацию. Это очень важные навыки не только в геометрии, но и в жизни в целом. Они помогают нам принимать обоснованные решения, решать проблемы и развивать наше интеллектуальное мышление.
И, наконец, леммы не только полезны, но и увлекательны! Каждое новое лемма — это новое открытие, новая загадка, которую мы можем разгадать. Искать решения и находить новые идеи — это захватывающий процесс, который может увлечь нас и приносить радость от получения новых знаний и навыков.
Таким образом, леммы являются неотъемлемой частью геометрии и важным инструментом для понимания и доказательства сложных теорем. Они помогают нам разбить сложные задачи на более простые и понятные части, упрощают доказательства, развивают умственные способности и приносят радость от открытия новых знаний. Так что давайте вместе изучать и использовать леммы, чтобы глубже понять искусство геометрии!
Упрощение доказательств
Доказательства в геометрии могут быть сложными и запутанными, требующими большого количества логических шагов. Однако, существуют способы упростить доказательства, чтобы они были более понятными и достижимыми. В этой статье мы рассмотрим несколько подходов к упрощению доказательств в геометрии.
1. Применение известных лемм и теорем
Одним из способов упростить доказательство является использование известных лемм и теорем. Если мы можем связать наше утверждение с уже доказанными результатами, то это может существенно упростить наше доказательство. Например, если мы знаем теорему Пифагора, то можем использовать ее для доказательства свойств треугольников.
2. Использование аналогий
Иногда, чтобы понять и доказать новое утверждение, полезно сделать аналогию с уже известными фактами. Например, если требуется доказать равенство двух углов, можно рассмотреть сходство с уже известной ситуацией, в которой углы также равны.
3. Разбиение задачи на более мелкие части
Большие задачи могут быть сложными для доказательства, поэтому их полезно разбить на несколько более простых частей. Затем можно доказывать эти части по отдельности и объединить их для получения окончательного результата. Это позволит нам сосредоточиться на каждом шаге доказательства и избежать сложности доказательства всей задачи сразу.
4. Использование геометрических построений и изображений
Иногда сложные геометрические доказательства можно упростить, представив задачу в графическом виде. Геометрические построения и рисунки могут помочь нам лучше визуализировать и понять свойства фигур и объектов, что облегчит нам доказательство. Они могут также помочь нам найти более простые идеи и особенности, которые могут быть ключевыми для доказательства.
5. Использование аналитической геометрии
В некоторых случаях использование аналитической геометрии может упростить доказательство. Это позволяет нам использовать методы и техники алгебры и анализа для работы с геометрическими объектами. Аналитическая геометрия может помочь найти уравнения и свойства объектов, что облегчит их доказательство.
Построение новых теорем
Дорогой читатель, сегодня я хотел бы рассказать тебе о захватывающем и зачастую магическом процессе построения новых теорем в геометрии. Это процесс, который открывает новые горизонты, расширяет наши знания и вдохновляет на дальнейшие открытия. Давай вместе погрузимся в мир математики и узнаем, каким образом строятся новые теоремы.
Когда геометры начинают работу над новой теоремой, их воображение и художественное видение сходятся вместе. Они начинают с непосредственного восприятия пространства, представляя себе различные геометрические формы, фигуры и объекты. Здесь важно позволить себе быть творческими, разыгрывать ситуации и давать полету своей фантазии. Ведь именно из этого «игрового процесса» рождаются идеи.
После того, как геометры нарисовали ряд фигур и объектов, они начинают изучать их свойства. Они задают себе вопросы о присущих им характеристиках и взаимоотношениях. Необходимо глубоко погрузиться в каждую деталь, изучить ее до мельчайших подробностей. В процессе изучения свойств фигур возникают гипотезы о возможных взаимосвязях и закономерностях.
Затем геометры создают предположение или гипотезу, основываясь на своей интуиции и знаниях. Это предложение о свойствах фигур и их взаимосвязях может быть подтверждено или опровергнуто, но в любом случае это является отправной точкой для развития всей теоремы.
Дальнейший процесс включает в себя доказательство гипотезы. Геометры используют уже существующие математические знания и методы для выяснения, верно ли то, что они предположили. Они анализируют доказательство в каждой точке, ищут ошибки и уточняют подробности. Это требует терпения, внимательности и умения думать логически.
И наконец, когда доказательство гипотезы завершено, геометра может с уверенностью заявить, что предложенная им теорема является истинной. Он может поделиться своим открытием с научным сообществом и получить признание за свою работу.
Как ты думаешь, дорогой читатель, почему строительство новых теорем так важно? Да потому что это позволяет нам понять глубинные законы природы, расширить наши знания о геометрии и создать фундамент для новых открытий. Необходимость в новых теоремах всегда присутствует, так как наш мир бесконечно изменчив и полон загадок итайнств.
Так что, дорогой читатель, возможно, именно ты станешь тем геометром, который создаст новую теорему и изменит наше понимание мира! Верь в себя, будь творческим, исследуй и экспериментируй. Ничто не помешает тебе строить новые теоремы и расширять границы нашего знания!
Углубление понимания геометрических концепций
Геометрия, как наука, изучает пространственные фигуры и их свойства. Она позволяет нам понять, как взаимодействуют объекты в пространстве и построить логические последовательности, чтобы решить сложные геометрические проблемы. Но иногда понимание геометрических концепций может быть непростым заданием. В этом тексте я попытаюсь помочь вам углубить свое понимание этой науки, чтобы геометрия стала более доступной и интересной для вас.
Построение основных понятий
Одним из основных понятий в геометрии является понятие «точка». Точка — это самое простое понятие в геометрии. Она не имеет размера и не занимает место, но она служит основой для построения всех геометрических фигур. Мы можем представить точку как некий «отметочный знак» на бумаге или в пространстве.
Другим важным понятием является «линия». Линия — это набор бесконечного числа точек, расположенных в одну прямую. Линия также не имеет толщины, она просто занимает место в пространстве. Линии могут быть прямыми, кривыми или чередующимися.
Прямая — это линия, у которой все точки лежат на одной прямой. Прямая очень важна в геометрии, она используется для построения углов и других фигур.
Углы и их свойства
Угол — это область в пространстве, образованная двумя лучами, которые протягиваются из общей точки, называемой вершиной угла. Углы могут быть острыми, прямыми, тупыми или полными.
Острый угол — это угол, который меньше 90 градусов. Прямой угол — это угол, который равен 90 градусам. Тупой угол — это угол, который больше 90 градусов. Полный угол — это угол, который равен 180 градусам.
Углы также могут быть комбинированы, например, сумма двух углов может быть равна 180 градусам (следовательно, они называются смежными углами) или 90 градусам (следовательно, они называются вертикальными углами).
Построение сложных фигур
Еще одним интересным аспектом геометрии является построение сложных фигур. Например, треугольник — это фигура, которая состоит из трех линий, соединенных в трех точках. Треугольник может быть различных типов, таких как равносторонний треугольник, равнобедренный треугольник или разносторонний треугольник.
Мы также можем построить многоугольник, который имеет более трех сторон. Многоугольники также могут быть различных типов, таких как прямоугольник, ромб или квадрат.
Заключение
Геометрия — это удивительная наука, которая позволяет нам понять мир вокруг нас. Расширение нашего понимания геометрических концепций поможет нам принимать информированные решения и решать сложные задачи. Надеюсь, что этот текст помог вам углубить свое знание геометрии и сделал ее более интересной и доступной для вас.
Примеры лемм в геометрии

Лемма о сегменте
Лемма о сегменте, также известная как лемма о перпендикуляре к хорде, является одной из основных лемм в геометрии. Она утверждает, что перпендикуляр, проведенный из центра окружности к хорде, делит эту хорду пополам. Это утверждение используется в доказательстве теоремы о касательной, а также во многих других геометрических задачах.
Лемма о угле в окружности
Лемма о угле в окружности утверждает, что угол, образованный хордой и касательной, проведенной к окружности из точки касания, равен половине угла, под которым эта хорда полностью отсекает окружность. Эта лемма широко используется в доказательстве теоремы о касательной, а также в других геометрических задачах, связанных с окружностями.
Лемма об антисимедиане
Лемма об антисимедиане утверждает, что в прямоугольном треугольнике биссектриса катета является антисимедианой к гипотенузе. Эта лемма используется в доказательстве теоремы о медиане, а также при решении геометрических задач с треугольниками.
Лемма о трех перпендикулярах
Лемма о трех перпендикулярах утверждает, что перпендикуляры, опущенные из середин сторон треугольника на противоположные стороны, пересекаются в одной точке, которая является центром окружности, описанной вокруг данного треугольника. Эта лемма используется при доказательстве теоремы о центре окружности, описанной вокруг треугольника, а также при решении других геометрических задач.
Все эти леммы, хоть и являются вспомогательными утверждениями, играют важную роль в геометрии. Они помогают доказывать более сложные теоремы и находить решения геометрических задач. Изучение и понимание этих лемм помогает развивать логическое мышление и навыки работы с геометрическими фигурами.
Лемма о прямоугольнике
Лемма о прямоугольнике утверждает, что если у нас есть четырехугольник, у которого противоположные стороны равны между собой и перпендикулярны, то этот четырехугольник является прямоугольником. Другими словами, если у нас есть четыре стороны AB, BC, CD и DA, где AB = CD и BC = AD, и углы ABC и BCD являются прямыми, то мы получаем прямоугольник.
Это утверждение может быть доказано с помощью различных методов, например, через свойства равнобедренного треугольника или применением теоремы Пифагора. В итоге, используя данную лемму, мы можем утверждать, что если мы имеем четырехугольник с такими свойствами, то он обязательно является прямоугольником.
Лемма о прямоугольнике полезна при решении различных задач, связанных с прямоугольником. Например, она может быть использована для доказательства теоремы о серединах сторон, когда точки, соединяющие середины сторон прямоугольника, образуют еще один прямоугольник. Также с ее помощью можно описывать свойства диагоналей прямоугольника и доказывать теоремы о параллельности его сторон.
Лемма о прямоугольнике является фундаментальным понятием в геометрии, которое помогает установить связь между различными свойствами прямоугольника. Она позволяет нам рассматривать прямоугольник как особый четырехугольник, в котором все углы равны 90 градусам и противоположные стороны равны. Это отличительное свойство прямоугольника делает его особенно полезным в различных областях, таких как архитектура, инженерия и математика.
Пример:
Рассмотрим следующую теорему: Углы смежные вписанные на одной дуге равны.
Чтобы доказать эту теорему, можно использовать лемму: Если две окружности пересекаются, то угол между хордами, соединяющими точки пересечения с центром, равен половине суммы дуг, заключенных между этими хордами.
Применяем лемму к нашей задаче: на одной дуге имеем два угла, образованные двумя смежными вписанными углами. Применяя лемму, представляем эти углы как углы между хордами, соединяющими точки пересечения с центром, и получаем, что эти углы равны половине суммы дуг, заключенных между этими хордами.
Таким образом, используя лемму, мы доказали, что углы смежные вписанные на одной дуге равны.