Определение линейной функции
Я хочу, чтобы ты представил, что линейная функция – это своего рода математический инструмент, который помогает нам описывать различные зависимости в реальном мире. Можно сказать, что она связывает две переменные: x и y. Представь, что x – это некая величина, которая измеряется по оси горизонтально, а y – это другая переменная, которая измеряется по оси вертикально. Важно, чтобы мы понимали, что одна переменная зависит от другой.
Просто представь себе, что ты измеряешь количество съеденных конфет в зависимости от времени. Количество съеденных конфет будет зависеть от того, сколько времени прошло. Чем больше времени прошло, тем больше конфет ты съел. В этом случае можешь представить количество конфет как переменную y, а время – как переменную x.
Теперь, когда ты представил, как линейная функция работает, давай обратимся к уравнению y = kx + b. Начнем с k – коэффициента при переменной x. Он определяет наклон линии графика функции. Если k положительный, то линия будет наклонена вверх, если отрицательный – то вниз. Величина k также определяет, насколько быстро меняется значение y в зависимости от изменения значения x.
Свободный член b отображает точку, где график функции пересекает ось y. Если b больше нуля, то график будет находиться выше оси x, а если меньше нуля – ниже. Если b равно нулю, то график будет проходить через начало координат.
Теперь чувствуешь себя комфортно с понятием линейной функции? Это просто инструмент, который помогает нам понять и предсказать, как одна переменная зависит от другой. Именно такой подход используется во многих научных и профессиональных областях, а также в повседневной жизни. Надеюсь, ты будешь использовать это знание, чтобы лучше разбираться в мире. Если у тебя есть какие-либо вопросы, не стесняйся спрашивать!
График линейной функции
Основой графика линейной функции является прямая линия. Интересно то, что всегда когда мы решаем линейное уравнение и строим график функции, получаем прямую линию. Необычно правда?! Такая форма графика может показать различные ситуации в реальной жизни, такие как изменение скорости автомобиля, стоимость товара или температуру.
Как строить график линейной функции?
Для построения графика линейной функции нам понадобится как минимум две точки на плоскости. Эти точки определяются подстановкой различных значений переменной в наше уравнение и рассчитываются значения функции.
Давайте рассмотрим пример. Пусть у нас есть линейная функция y = 2x + 1. Мы можем выбрать любое значение для x и вычислить соответствующее y. Например, когда x = 0, y = 2 * 0 + 1 = 1, а когда x = 1, y = 2 * 1 + 1 = 3.
Мы получили две точки (0, 1) и (1, 3). Теперь осталось соединить их прямой линией на координатной плоскости. Готово! У нас есть график линейной функции.
Понимание графика линейной функции помогает нам анализировать и понимать различные показатели в реальной жизни, а также делать прогнозы и принимать решения на основе этих данных. Конечно же, это только один из инструментов математики, но очень полезный и интересный.
Нахождение коэффициентов линейной функции
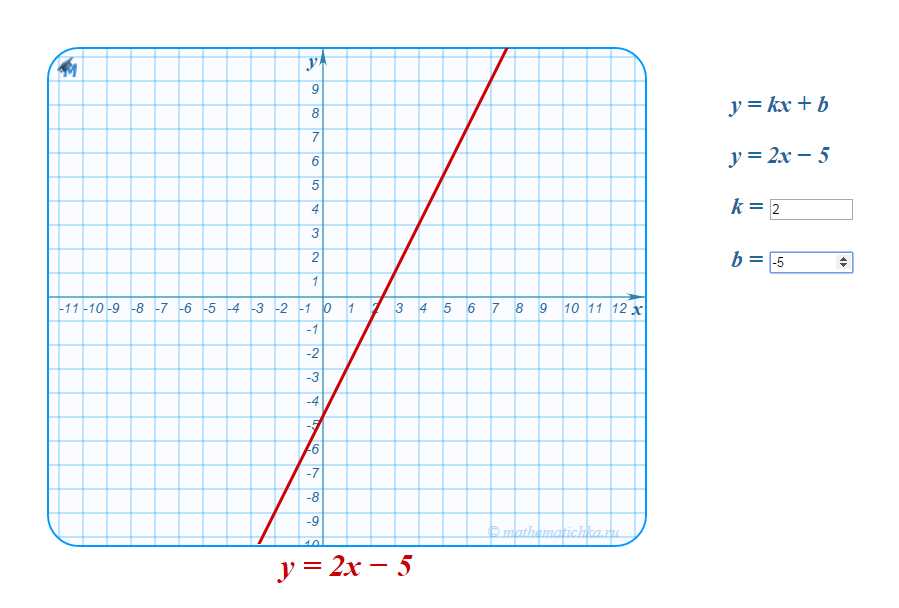
Чтобы найти коэффициенты k и b линейной функции, нужно использовать информацию о двух точках, через которые проходит прямая или о наклоне и точке, через которую проходит прямая.
Например, если даны точки (x1, y1) и (x2, y2), мы можем использовать формулу для нахождения наклона прямой:
k = (y2 — y1) / (x2 — x1)
После нахождения наклона k, мы можем найти b, подставив координаты одной из точек в уравнение прямой y = kx + b и решив уравнение относительно b:
b = y — k * x
Таким образом, мы можем легко найти коэффициенты линейной функции, используя информацию о точках или наклоне и точке, через которую проходит прямая. Это позволяет нам построить и анализировать линейные функции, предсказывать значения y для заданных x и использовать эти функции в реальной жизни.
Допустим, у нас есть две точки (1, 3) и (4, 9), через которые проходит прямая. Мы можем найти наклон k:
k = (9 — 3) / (4 — 1) = 2
Затем, используя координаты любой из точек (например, точки (1, 3)), мы можем найти b:
b = 3 — 2 * 1 = 1
Таким образом, уравнение прямой будет выглядеть y = 2x + 1. Это означает, что при увеличении x на единицу, значение y увеличивается на 2. Прямая будет проходить через точки (1, 3) и (4, 9).
Итак, знание процесса нахождения коэффициентов линейной функции позволяет нам легко анализировать и использовать эти функции в различных задачах. Необходимо помнить, что линейные функции широко применяются в жизни и позволяют нам моделировать различные зависимости между переменными.
Прямая пропорциональность
Давайте рассмотрим пример, чтобы лучше понять прямую пропорциональность. Представьте, что вы идете в магазин за фруктами. Вы можете купить 2 кг яблок за 100 рублей. Если вы хотите купить 4 кг яблок, сколько это будет стоить? Правильно, 200 рублей! Количество яблок увеличилось в 2 раза, поэтому и цена увеличилась в 2 раза.
Такая пропорциональность может быть представлена с помощью линейной функции. Формулой для линейной функции в прямой пропорциональности является y = kx, где y — зависимая переменная (в данном случае стоимость яблок), x — независимая переменная (в данном случае количество яблок), и k — постоянный коэффициент пропорциональности.
Итак, когда мы говорим о прямой пропорциональности, мы говорим о пересекающихся линейных функциях, где коэффициенты пропорциональности одинаковы. Если мы построим график этой функции, то получим прямую линию, проходящую через начало координат.
Прямая пропорциональность широко используется в нашей повседневной жизни. Например, когда мы едем на машине, чем больше мы проезжаем, тем больше мы тратим бензина. Это пример прямой пропорциональности, где пройденное расстояние и потребление топлива связаны друг с другом.
Какие еще примеры прямой пропорциональности вы можете привести из своего опыта? Возможно, вы заметили, что чем больше времени вы проводите на изучении математики, тем лучше вы становитесь в ней. Или, может быть, у вас есть любимая формула для выпечки печенья, и вы заметили, что если увеличить количество ингредиентов, количество печенья увеличивается в том же самом отношении.
Прямая пропорциональность — это концепция, которую мы можем встретить повсюду. Будьте внимательны к таким связям между величинами и запомните, что когда одна величина увеличивается, другая тоже увеличивается в том же отношении. Это важное и полезное знание, которое поможет вам лучше понять мир вокруг вас.
Обратная пропорциональность
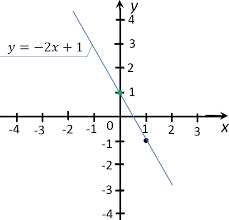
Так вот, обратная пропорциональность — это особенность, когда два значения изменяются таким образом, что когда одно увеличивается, другое уменьшается, и наоборот. Это значит, что одно значение растет, а другое падает, и наоборот.
Представляешь, ты идешь в магазин и покупаешь батон хлеба. Все просто, правда? Но давай посмотрим на эту ситуацию с математической точки зрения. Чем больше батонов ты покупаешь, тем меньше стоимость одного батона. А если ты решаешь купить меньше батонов, то цена за один батон будет больше. Здесь и происходит обратная пропорциональность — количество батонов и стоимость за один батон меняются в противоположные стороны.
Можно сказать, что обратная пропорциональность — это как в радио. Если усилить громкость, то шум станет громче, а если уменьшить громкость, то шум станет тише. Так и в математике: увеличивая одно значение, мы уменьшаем другое, и наоборот.
Давай рассмотрим еще один пример. Представь, ты катишься на велосипеде. Чем быстрее ты крутишь педали, тем больше расстояние, которое ты преодолеваешь за определенное время. Однако, если ты начинаешь крутить педали медленнее, то расстояние, которое ты преодолеваешь, увеличивается. Здесь мы вновь видим обратную пропорциональность: скорость, с которой ты крутишь педали, и расстояние, которое ты проезжаешь, движутся в противоположных направлениях.
Ты уже начал понимать, что такое обратная пропорциональность, не так ли? Она встречается во многих сферах нашей жизни. Подумай, где еще ты мог бы заметить обратную пропорциональность? Может быть, во времени, которое ты тратишь на выполнение задания, и качестве результата? Или в объеме упражнений, которые ты выполняешь, и физической форме?
Короче говоря, обратная пропорциональность — это увлекательное понятие, которое помогает нам разобраться во многих ситуациях, где два значения связаны между собой. Иногда она может показаться сложной, но рассмотрение примеров из нашей повседневной жизни помогает нам лучше понять это понятие.
Так что следующий раз, когда ты увидишь, что два значения движутся в противоположных направлениях, подумай о том, что это могут быть обратно пропорциональные величины. И помни, что в математике нет ничего сложного, если мы ориентируемся на реальные ситуации и делаем их понятными.
Линейная функция: понятие и примеры
Коэффициент k называется коэффициентом наклона или угловым коэффициентом. Он определяет, насколько быстро возрастает или убывает значение функции с изменением аргумента x. Если k положительное число, то функция возрастает; если k отрицательное число, то функция убывает.
Примеры линейных функций:
- y = 2x + 3
- y = -0.5x + 1
- y = 4x
В таблице ниже представлены значения функции для различных значений аргумента x для функции y = 2x + 3:
| x | y = 2x + 3 |
|---|---|
| 0 | 3 |
| 1 | 5 |
| 2 | 7 |
| 3 | 9 |
Из таблицы видно, что с каждым увеличением значения x на 1, значение y увеличивается на 2. Это связано с коэффициентом наклона k, который равен 2 в данном случае.
Линейные функции широко применяются в математике, физике, экономике и других областях для описания прямолинейных зависимостей между величинами.