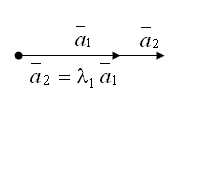
Ты уже сталкивался с понятием «линейная комбинация»? Если нет, то сейчас я все тебе расскажу. Линейная комбинация — это математическое понятие, которое позволяет нам комбинировать и складывать различные элементы векторного пространства с помощью умножения на скаляры и сложения. Звучит сложно? Не переживай, я всё объясню простыми словами!
Линейная комбинация имеет важное применение в различных областях, включая физику, экономику, информатику и другие. Она помогает нам моделировать реальные процессы, находить решения систем уравнений и даже создавать алгоритмы компьютерных программ. Это мощный инструмент, который позволяет нам анализировать и использовать данные эффективно.
Давай разберемся подробнее, как работает линейная комбинация и посмотрим на несколько примеров ее применения. Приготовься к увлекательному путешествию в мир математики и приложений!
Определение линейной комбинации
Давай рассмотрим пример. Представь, что у тебя есть два вектора: v1 = (2, 3) и v2 = (4, 1). Теперь мы можем построить линейную комбинацию этих векторов с помощью коэффициентов a и b, где a и b могут быть любыми числами.
Линейная комбинация этих векторов будет выглядеть следующим образом:
v = a * v1 + b * v2 = (a * 2, a * 3) + (b * 4, b * 1) = (2a + 4b, 3a + b)
То есть, вектор v будет представлять собой сумму первого вектора, умноженного на коэффициент a, и второго вектора, умноженного на коэффициент b.
Зачем нам нужна линейная комбинация? Она позволяет нам выразить один вектор через другие векторы и описывает линейные зависимости между векторами. Например, если вектор v может быть представлен как линейная комбинация векторов v1 и v2, то это означает, что он находится в плоскости, определенной этими векторами.
Также линейная комбинация используется для решения систем линейных уравнений. Например, если у нас есть система уравнений с неизвестными a и b:
a * v1 + b * v2 = (x, y)
То мы можем найти их значения, выразив их через линейную комбинацию векторов v1 и v2.
Линейная комбинация — это мощный инструмент для изучения и анализа векторов и их взаимосвязей. Она позволяет нам понять, как векторы влияют друг на друга и как они могут быть использованы для решения различных задач. Поэтому, понимание определения и применения линейной комбинации является важным для развития многих областей науки и техники.
Концепция линейной комбинации

Линейная комбинация — это математическая операция, в ходе которой два или более объекта объединяются с помощью линейных комбинаторных коэффициентов. Звучит сложно? Давайте посмотрим на примере.
Представьте себе, что у вас есть два вектора: v1 = (2, 3) и v2 = (-1, 4). Что произойдет, если мы возьмем 2*v1 — 3*v2? Мы просто умножим каждый компонент вектора v1 на 2 и каждый компонент вектора v2 на -3, а затем сложим полученные результаты. Таким образом, мы получим новый вектор.
Почему это называется «линейной» комбинацией? Потому что линейная комбинация сохраняет свойства линейности. Другими словами, если вы возьмете два вектора v1 и v2, и выполните с ними линейную комбинацию с помощью коэффициентов a и b, то результатом будет вектор, который можно представить в виде a*v1 + b*v2. Это линейное сочетание компонентов векторов, которое позволяет нам работать с ними с легкостью и эффективностью.
Линейная комбинация имеет множество применений. Она используется для решения систем линейных уравнений, нахождения базисных векторов, построения линейных преобразований и многого другого. Она помогает нам описывать и анализировать сложные математические объекты, используя простые и понятные методы.
Так что, несмотря на сложность математики, линейная комбинация — это простой и мощный инструмент, который позволяет нам объединять и работать с различными математическими объектами. Ее понимание и применение открывают перед нами множество возможностей и расширяют границы нашего знания.
Понятие векторов

Вектор можно представить как стрелку, которая обладает определенной длиной и направлением. Длина вектора называется его модулем, а направление указывает на то, в какую сторону вектор указывает. Векторы могут быть одномерными (содержащими только числовое значение) или многомерными (содержащими несколько числовых значений).
Одной из важных операций над векторами является их сложение или вычитание. Векторы могут складываться друг с другом, если они имеют одинаковую размерность. При сложении векторов их компоненты складываются поэлементно и образуют новый вектор. Аналогично, при вычитании векторов их компоненты вычитаются поэлементно.
Однако векторы также могут участвовать в другой важной операции — линейной комбинации. Линейная комбинация векторов возникает при умножении каждого из векторов на некоторое число и последующем сложении полученных произведений. Результатом такой операции является новый вектор, который может представлять, например, сумму или среднее значение нескольких физических величин.
Векторы находят применение в различных областях, таких как физика, геометрия, экономика, компьютерная графика и многие другие. Они позволяют наглядно представлять и анализировать различные явления и процессы. Благодаря своей гибкости и мощи, векторы стали неотъемлемой частью математики и играют важную роль в развитии науки и технологий.
Линейные комбинации и коэффициенты

Прежде чем мы перейдем к объяснению линейных комбинаций и их коэффициентов, давайте сначала рассмотрим, что они в значении математики. Это может показаться сложным понятием, но я уверен, что мы сможем разобраться вместе!
Линейная комбинация — это сумма произведений набора векторов на соответствующие им коэффициенты. Иными словами, это способ объединить несколько векторов, присвоив каждому из них определенный вес или значение. Понимание линейных комбинаций имеет большое значение в различных областях математики и физики.
Чтобы лучше понять, что такое коэффициенты в линейной комбинации, давайте рассмотрим пример. Представьте, что у нас есть два вектора, A и B, и мы хотим получить их линейную комбинацию. Мы можем использовать коэффициенты, чтобы определить, сколько каждого вектора мы будем добавлять в общую сумму.
Допустим, мы выбрали коэффициенты 2 для вектора A и 3 для вектора B. Наше выражение для линейной комбинации будет выглядеть следующим образом:
2A + 3B
Теперь мы можем начать вычисления. Умножаем коэффициенты на соответствующие векторы и складываем результаты:
2A = (2 * A)
3B = (3 * B)
Затем мы складываем полученные значения:
2A + 3B = (2A) + (3B)
Результат линейной комбинации зависит от выбранных коэффициентов. Если мы поменяем коэффициенты и выберем, например, 3 для вектора A и 2 для вектора B, получим следующее:
3A + 2B = (3 * A) + (2 * B)
Как мы видим, линейные комбинации могут быть очень гибкими и могут применяться для разных задач в математике, физике и других областях. Они позволяют нам комбинировать и учитывать вклад разных величин, чтобы получить общий результат.
Надеюсь, теперь вы понимаете, что такое линейные комбинации и как использовать коэффициенты в этом процессе. Какие мысли у вас по этому поводу? Вы можете представить какие-то реальные примеры или задачи, где это применяется? Делитесь своими мыслями!
Линейная комбинация: определение и применение

Формально, линейная комбинация векторов определяется следующим образом: для данных векторов v1, v2, …, vn и их коэффициентов с1, c2, …, cn, их линейная комбинация записывается как:
c1 * v1 + c2 * v2 + … + cn * vn
Линейная комбинация векторов может быть полезной во многих областях науки и промышленности. Например, в физике, линейная комбинация векторов может использоваться для описания сложных движений или сил в системе.
Также линейная комбинация может использоваться для решения систем линейных уравнений. Если заданная система линейных уравнений имеет решение, то это решение можно представить в виде линейной комбинации векторов, которые являются базисом пространства решений.
Все это делает линейную комбинацию важным инструментом в линейной алгебре и ее приложениях.




