В математике неравенства играют важную роль, позволяя сравнивать и определять отношения между числами и переменными. Линейные и квадратные неравенства являются основными типами неравенств, с которыми сталкиваемся в различных областях жизни. Линейные неравенства имеют вид ax + b > c или ax + b < c, где a, b и c - константы, а x - переменная. Они позволяют определять диапазоны значений переменных, удовлетворяющих заданным условиям. Квадратные неравенства, в свою очередь, выражают зависимость между квадратным уравнением и неравенством. Понимание этих понятий и примеров их применения помогает решать различные задачи, связанные с математикой и реальным миром.
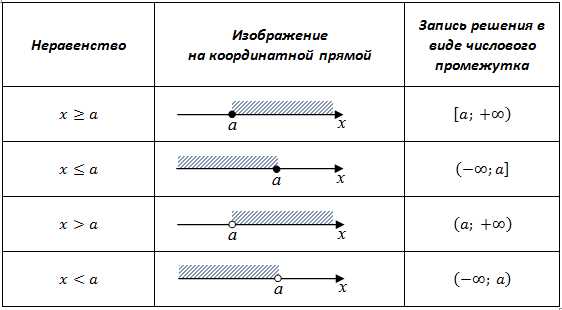
Линейные неравенства
Представим, что у нас есть два числа – а и b, и мы хотим сравнить их между собой с помощью неравенства. Например, мы можем сказать, что а больше, чем b, записывая это как а > b. Это является линейным неравенством, поскольку и a, и b – это линейные выражения (они состоят из переменных и констант, объединенных с помощью арифметических операций).
Линейные неравенства играют огромную роль в математике и решаются с помощью различных методов. Во-первых, мы можем использовать алгебраические операции, чтобы упростить уравнение и найти значения переменных, удовлетворяющие неравенству. На примере а > b мы можем постепенно преобразовывать это неравенство, добавляя или вычитая числа, чтобы найти диапазон значений, при которых неравенство выполняется.
Например, если у нас есть неравенство 2x + 3 > 5, мы можем вычесть 3 из обеих сторон и получить 2x > 2. Затем мы можем разделить обе стороны на 2 и получить x > 1. Таким образом, решением этого неравенства будет любое число больше 1.
Кроме того, для решения линейных неравенств можно использовать графический подход. В этом случае мы строим график линейного выражения и определяем область, которая удовлетворяет неравенству. На графике неравенство а > b будет представлено полуплоскостью, расположенной выше линии, соответствующей линейному выражению a = b.
Линейные неравенства широко используются в различных областях науки и экономики. Например, они могут использоваться для определения диапазона значений, при которых функция положительна или отрицательна, или для моделирования ограничений в задачах оптимизации.
Определение
Линейное неравенство имеет следующий вид: ax + b > c, где a, b и c — это числа, а x — это переменная. Решение линейного неравенства представляет собой диапазон значений x, при которых неравенство выполняется.
Квадратное неравенство, например, x^2 — 4x + 3 < 0, имеет более сложную форму. Оно состоит из квадратного выражения с переменной x и константами. Решение квадратного неравенства - это диапазон значений x, при которых неравенство выполняется.
Для решения линейных и квадратных неравенств необходимо использовать алгебраические методы. При решении линейных неравенств мы применяем операции, такие как сложение, вычитание, умножение и деление, чтобы изолировать переменную. При решении квадратных неравенств мы используем факты о поведении таких функций, как квадраты и корни.
Линейные и квадратные неравенства являются важными инструментами в различных областях математики и естественных наук. Они используются, например, для анализа функций, моделирования реальных процессов и решения практических задач.
Примеры
Поговорим о некоторых конкретных примерах линейных и квадратных неравенств, чтобы лучше понять их применение в реальной жизни. Давайте начнем со знакомого нам неравенства «x < 5". Это означает, что значение переменной x должно быть меньше 5. Например, если x = 3, то условие неравенства выполняется, так как 3 меньше 5. Однако, если x = 7, то условие неравенства не выполняется, так как 7 не меньше 5.
Еще один пример линейного неравенства — «2x + 3 > 9». Чтобы решить это неравенство, мы сначала вычитаем 3 из обеих сторон: «2x > 6». Затем делим обе части на 2: «x > 3». Это значит, что значение x должно быть больше 3. Например, если x = 4, то условие неравенства выполняется, так как 4 больше 3. Но если x = 2, то условие неравенства уже не выполняется, так как 2 меньше 3.
Перейдем к квадратным неравенствам. Рассмотрим квадратное неравенство «x^2 — 4x > 0». Чтобы решить его, мы сначала находим корни квадратного уравнения, которым равно выражение в левой части неравенства. Здесь у нас x^2 — 4x = 0, а корни этого уравнения равны 0 и 4. Теперь мы можем построить числовую ось и отметить эти корни. Затем анализируем интервалы между корнями и проверяем знак выражения на каждом из интервалов. Результатом будет, что неравенство выполняется на интервалах (-∞,0) и (4,∞).
Возможно, эти примеры показали вам, что линейные и квадратные неравенства имеют широкое применение в различных областях жизни. Они могут использоваться для нахождения диапазонов значений переменных, проверки условий задач, анализа данных и многого другого. Будет ли то определение допустимой стоимости товара, выяснение, какие значения переменных удовлетворяют условиям задачи, или нахождение интервалов, когда функция положительна или отрицательна, неравенства помогают нам лучше понять и анализировать мир вокруг нас.
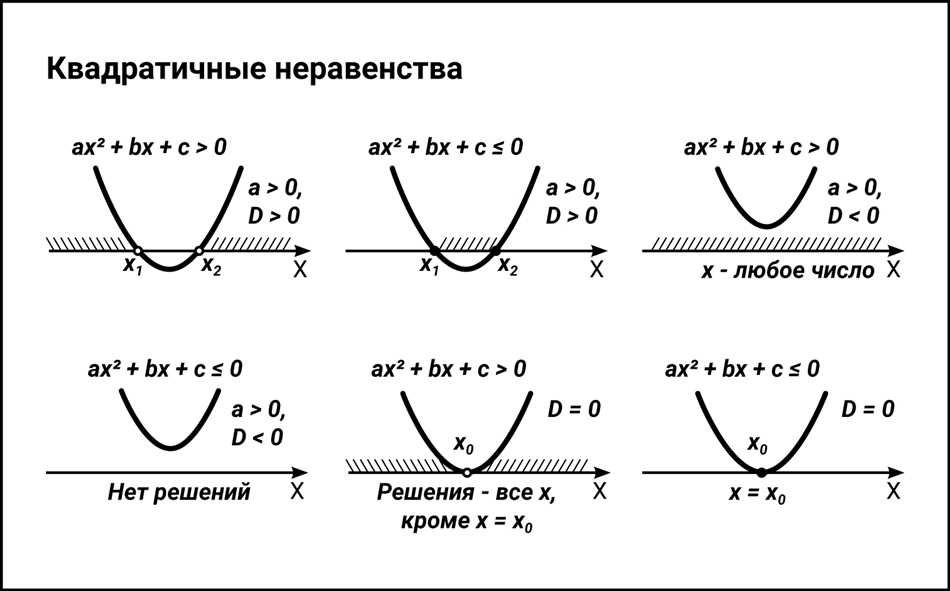
Квадратные неравенства
ax2 + bx + c > 0
где a, b и c — коэффициенты, а x — переменная.
Квадратные неравенства используются для решения различных проблем, где существует ограничение на значения переменной. Например, они могут быть применены для нахождения интервала времени, когда функция сохраняет положительные значения или когда равновесие между затратами и доходами достигается.
Как решать квадратные неравенства? В основном этот процесс состоит из нескольких шагов:
- Приведите неравенство к стандартному виду ax2 + bx + c > 0.
- Решите соответствующее уравнение ax2 + bx + c = 0.
- Постройте график уравнения на числовой оси, отметив корни на графике.
- Определите знаки коэффициентов a, b и c и определите интервалы, где уравнение больше нуля или меньше нуля.
- Найдите решение, основываясь на интервалах, где уравнение больше нуля или меньше нуля, а также на графике уравнения.
Квадратные неравенства имеют множество применений в реальной жизни. Они могут использоваться для поиска интервалов времени, когда функция будет положительной или отрицательной, для определения диапазона значений переменной, чтобы функция оставалась положительной или отрицательной, и многого другого.
Итак, квадратные неравенства — это мощный инструмент в математике, который позволяет решать задачи, связанные с ограничениями и интервалами. Необходимость решения квадратного неравенства возникает довольно часто, поэтому понимание этой концепции может быть полезно.
Определение
Линейные неравенства представляют собой неравенства с переменными, у которых степени равны 1. Например:
- 2x + 3 > 5
- -4y + 2 ≤ 10
Квадратные неравенства, в свою очередь, содержат квадрат переменной. Например:
- x^2 — 4 > 0
- 2y^2 + 5y — 3 ≤ 0
Основная задача решения таких неравенств состоит в определении множества значений переменных, при которых неравенство является истинным. Для решения линейных и квадратных неравенств используются различные методы, такие как алгебраические преобразования и графическое представление.
Линейные и квадратные неравенства широко применяются во многих областях, таких как физика, экономика, инженерия и т.д. Они позволяют выявить условия и ограничения при решении различных задач. Например, они могут помочь определить диапазон значений для достижения целей, оптимизации процессов и принятия правильных решений.
Линейные и квадратные неравенства: понятие и примеры

Линейное неравенство имеет следующий вид: ax + b < cx + d, где a, b, c и d - числа, а x - переменная. Решением этого неравенства будет множество значений переменной x, удовлетворяющих неравенству.
Пример линейного неравенства: 2x + 3 > 4x — 1. Для решения этого неравенства нужно собрать все x на одной стороне, а числа на другой. В данном случае получим: 3 + 1 > 4x — 2x. После преобразований получим: 4 > 2x, что равносильно выражению 2x < 4. Значит, решением неравенства будет неравенство x < 2.
Квадратное неравенство имеет вид: ax^2 + bx + c > 0 (или < 0), где a, b и c - числа, а x - переменная. Решением квадратного неравенства будет множество значений переменной x, для которых выполняется неравенство.
Пример квадратного неравенства: x^2 + 4x + 3 > 0. Для решения этого неравенства можно воспользоваться графиком функции y = x^2 + 4x + 3 и найти интервалы, на которых функция принимает положительные значения. В данном случае решением неравенства будет интервал (-∞, -3) ∪ (-1, +∞).