Логарифмический декремент затухания: понятие и применение

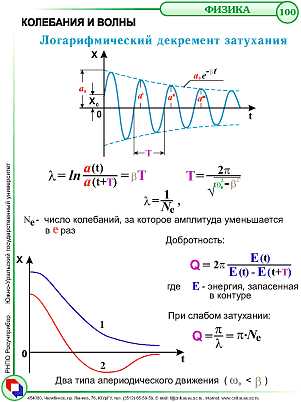
Когда мы говорим о колебаниях, невозможно не упомянуть такой важный параметр, как логарифмический декремент затухания. Такой термин может показаться сложным, но на самом деле, его определение и применение можно объяснить простыми словами.

Логарифмический декремент затухания — это параметр, характеризующий способность колебательной системы уменьшать свою амплитуду с каждым последующим колебанием. Он рассчитывается как отношение натурального логарифма амплитуды второго колебания к амплитуде первого колебания.

Понимание логарифмического декремента затухания позволяет ученым анализировать энергетические потери в системе и оптимизировать ее параметры. Это особенно важно в таких областях, как механика, электричество и сейсмология, где колебательные системы широко используются для измерения и контроля различных параметров.

Логарифмический декремент затухания: определение и применение

Здравствуйте! Давайте разберемся, что такое логарифмический декремент затухания и как он применяется в различных областях.

Логарифмический декремент затухания — это показатель затухания колебаний или амплитуды колебательного процесса с течением времени. Он определяется как разность логарифмов двух последовательных амплитуд колебаний. Обычно вычисляется по формуле:

ЛДЗ = ln(A_n/A_n+1) = 1/n * ln(A₀/A_n)

где A_n — амплитуда n-го колебания, A_n+1 — амплитуда следующего (n+1) колебания, A₀ — начальная амплитуда колебания.

Основное применение логарифмического декремента затухания связано с анализом колебательных систем, таких как электрические колебательные контуры, механические системы с затуханием и даже биологические процессы.

В электротехнике логарифмический декремент затухания применяется, например, для анализа амплитудно-частотной характеристики фильтров. Он позволяет оценить степень затухания сигнала при прохождении через фильтр и определить его частотные характеристики.

В механике логарифмический декремент затухания используется для оценки затухания колебаний в механических системах, таких как подвесные мосты или конструкции зданий и сооружений. Это помогает инженерам и архитекторам создавать более стабильные и безопасные конструкции.

Даже в биологических процессах логарифмический декремент затухания может иметь свое применение. Например, в медицине его можно использовать для анализа затухания сигналов в электрокардиограммах и определения степени активности сердечной деятельности.

Итак, логарифмический декремент затухания является важным показателем для анализа затухания колебаний и амплитуды в различных системах. Он применяется в электротехнике, механике и даже в медицине. Этот показатель помогает нам понять и оценить свойства и характеристики колебательных процессов.

Формула и расчет Логарифмического декремента затухания

Λ = ln(A_n / A_n+1)

где:

• Λ — логарифмический декремент затухания
• A_n — амплитуда n-го колебания
• A_n+1 — амплитуда следующего колебания

Таким образом, ЛДЗ можно рассчитать, сравнивая амплитуды последовательных колебаний в системе.

Расчет ЛДЗ может быть полезен в различных областях, таких как физика, электротехника, механика и т. д. Например, в электротехнике ЛДЗ используется для определения затухания колебаний в электрических цепях при наличии сопротивления. Это позволяет инженерам исследовать стабильность и эффективность работы электрических систем.

Еще одним практическим применением ЛДЗ является его использование в медицине для измерения затухания амплитуды колебаний сердца. Измерение ЛДЗ может дать представление о работе сердца и указать на наличие каких-либо проблем или нарушений в его функционировании.

Важно отметить, что расчет ЛДЗ может быть сложным и требует сведений об амплитудах колебаний в системе. Однако, с помощью современных вычислительных инструментов и математических методов, этот расчет может быть выполнен более эффективно и точно.

Таким образом, формула и расчет Логарифмического декремента затухания являются важным инструментом для изучения колебательных систем и имеют широкий спектр применения в различных областях науки и техники.

Применение логарифмического декремента затухания в физике

В физике логарифмический декремент затухания играет роль во многих областях, где требуется анализ колебательных систем. Этот понятие помогает нам понять и описать различные процессы и явления.

1. Колебательные системы

Логарифмический декремент затухания применяется для анализа колебательных систем. Например, в электрических цепях с колебательными контурами, резонансных фильтрах или системах с механическими колебаниями. Зная величину декремента затухания, мы можем определить резонансные частоты, количество энергии, передающейся от одной точки к другой, и другие параметры, связанные с колебаниями.

2. Акустика

В акустике логарифмический декремент затухания используется для изучения звука и его распространения. Он позволяет оценить потерю энергии звуковых волн в среде и определить характеристики звукопоглощающих материалов. Это важно при проектировании акустических систем, студий звукозаписи, концертных залов и других мест, где необходимо контролировать звуковое окружение.

3. Оптика

В оптике логарифмический декремент затухания используется для описания затухания световых волн при их распространении через оптически плотные среды. Этот параметр помогает нам понять потерю энергии света и изменение его интенсивности при прохождении через стекла, плазму или другие оптические материалы.

4. Электродинамика

В электродинамике логарифмический декремент затухания применяется для анализа колебательных систем в электрических и магнитных полях. Он позволяет определить потери энергии в системе и изучить ее динамическое поведение. Это важно при проектировании и расчете антенн, радиотехнических устройств и других электронных систем.

5. Механика

В механике логарифмический декремент затухания применяется для изучения затухания колебательных систем. Например, в амортизаторах автомобилей или маятниках. Зная этот параметр, мы можем оценить силы затухания, потери энергии и предсказать поведение системы во времени.

Таким образом, логарифмический декремент затухания имеет широкое применение в физике и является важным инструментом для анализа и понимания различных явлений и процессов. Он позволяет нам оценить потери энергии и изменение интенсивности колебаний при их распространении через различные среды и системы.

Применение в электронике

При проектировании фильтров, особенно в случае активных фильтров, логарифмический декремент затухания используется для определения частотных характеристик устройств и настройки резонансных частот. Он помогает инженерам и дизайнерам оптимизировать производительность фильтров и достичь требуемых частотных параметров.

Генераторы сигналов с использованием логарифмического декремента затухания могут быть настроены на определенные частоты и иметь заданную амплитуду колебаний. Это позволяет создавать стабильные и точные источники сигналов для различных приложений в электронике.

Логарифмический декремент затухания также играет важную роль в анализе электрических колебательных контуров и определении их параметров. Например, при работе с осциллографами, измерение логарифмического декремента затухания позволяет определить частоту колебаний, амплитуду и фазу сигналов.

В цифровых системах, таких как цифровые фильтры, логарифмический декремент затухания может быть использован для определения уровня шума и помех при обработке сигналов. Это помогает инженерам разрабатывать более эффективные фильтры для минимизации шума и улучшения качества сигналов.

Также логарифмический декремент затухания может быть использован для анализа и определения параметров акустических и оптических колебаний. Например, в видеосистемах он может быть использован для определения амплитуды и частоты видеосигналов.

В общем, использование логарифмического декремента затухания в электронике обеспечивает более точный анализ и настройку колебательных систем, что позволяет создавать более эффективные и качественные устройства и системы.

Логарифмический декремент затухания: определение и применение

ЛДЗ = ln(A₁/A₂) * (1/T)

где A₁ — амплитуда первого колебания, A₂ — амплитуда второго колебания, и T — период колебаний.

ЛДЗ находит широкое применение в различных областях. Например, в электронике он используется для определения параметров колебательных контуров и фильтров. В механике ЛДЗ помогает оценить характеристики колебательных систем, таких как маятники или подвесные мосты. Также ЛДЗ используется в акустике для описания затухания звуковых волн.

Для более сложных систем, с большим числом степеней свободы, ЛДЗ может быть сложно вычислить аналитически. В таких случаях используются численные методы решения уравнений движения или экспериментальные данные.

Применение логарифмического декремента затухания

• Определение параметров колебательных контуров и фильтров в электронике.
• Оценка характеристик механических систем с колебаниями, таких как маятники.
• Исследование затухания звуковых волн в акустике.
• Определение демпфирующих свойств материалов.
• Анализ процессов в системах с вынуждающей силой.