Знание математики играет важную роль в нашей жизни и нередко нам помогает в различных ситуациях. Один из важных математических инструментов — логарифмы. Но что это такое и как их применять?
Логарифм — это математическая функция, обратная к экспоненте. Он помогает решать сложные задачи, связанные с экспоненциальным ростом и десятичными степенями. Логарифмы широко применяются в финансовой аналитике, науке, технике и других областях.
В данном тексте мы рассмотрим определение логарифмов, их свойства и различные способы решения, которые помогут вам легко справиться с математическими проблемами, связанными с логарифмами.
Определение логарифма
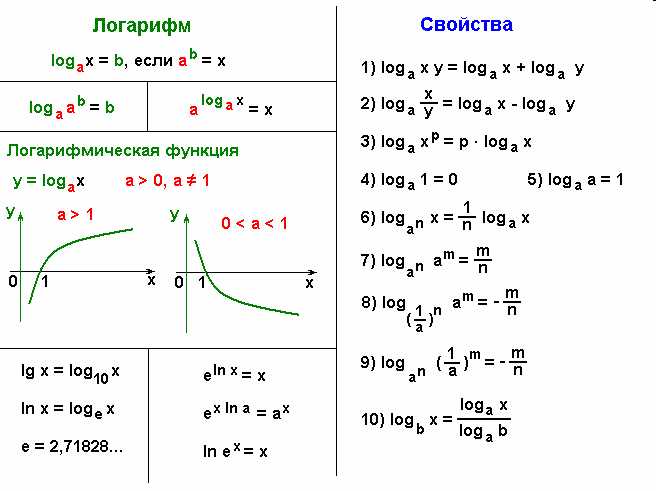
Логарифм может быть определен как функция, обратная к возведению числа в степень. Иными словами, логарифм – это показатель степени, к которому нужно возвести определенное число, чтобы получить другое число. Например, логарифм числа 100 по основанию 10 равен 2, потому что 10 возводим в степень 2 даёт 100.
Логарифмы очень широко используются в науке, инженерии, экономике и других областях. Они помогают сократить большие числа и уменьшить сложность вычислений. Например, при работе с очень большими или очень маленькими числами логарифмы позволяют представить их в более компактной форме.
Логарифмы также помогают в решении уравнений и находить неизвестные значения. Они помогают найти степень, в которую нужно возвести число, чтобы получить результат, или найти число по известному значению логарифма и основанию.
Теперь, когда вы знаете, что такое логарифм, вы можете задать себе вопрос – зачем мне знать это? Ответ прост: логарифмы помогают нам лучше понимать и анализировать мир вокруг нас. Они находят применение в финансовых расчетах, науке, технике и многих других областях. Знание логарифмов поможет вам стать более компетентным в этих областях и расширит ваше понимание математики в целом.
Когда мы говорим о логарифмах, мы не только решаем математические задачи, но и развиваем наше мышление и логическое мышление. Умение применять логарифмы в решении задач помогает нам развивать навыки анализа, критического мышления и решения проблем. Это очень важные навыки, которые помогут вам во всех сферах жизни.
Итак, друзья, помните, что логарифмы – это мощный инструмент, который помогает нам решать задачи, анализировать данные и развивать наше мышление. Не бойтесь этого понятия, а относитесь к нему с интересом и любопытством. Узнайте больше о логарифмах, и они откроют для вас новые возможности и перспективы в разных областях. Удачи в изучении логарифмов!
Свойства логарифмов
Первое важное свойство логарифма — это свойство равенства. Оно гласит, что если мы имеем логарифм от числа x по основанию a, и этот логарифм равен некоторому числу y, то мы можем записать это в виде уравнения: a^y = x. Это свойство позволяет нам переписывать логарифмы в виде экспонент.
Следующее свойство — это свойство перемножения. Если у нас есть два логарифма от одного и того же числа по одному и тому же основанию, мы можем перемножить их и записать это в виде логарифма от произведения исходных чисел: loga(x) + loga(y) = loga(x*y). Это свойство помогает нам упрощать сложные выражения и сокращать логарифмы.
Третье свойство — это свойство деления. Аналогично свойству перемножения, мы можем разделить два логарифма и записать это в виде логарифма от частного исходных чисел: loga(x) — loga(y) = loga(x/y). Это свойство также помогает нам упрощать выражения и сокращать логарифмы.
Следующее свойство — это свойство возведения в степень. Если у нас есть логарифм от числа x в некоторой степени n по основанию a, мы можем записать это в виде степени исходного числа: (loga(x))^n = x. Это свойство помогает нам преобразовывать логарифмы в степень и наоборот.
И наконец, последнее свойство — это свойство изменения основания. Если у нас есть логарифм от числа x по основанию a, мы можем записать это в виде логарифма того же числа по другому основанию b: loga(x) = logb(x) / logb(a). Это свойство помогает нам менять основание логарифма и переходить от одного основания к другому.
Важно помнить, что эти свойства могут быть использованы только при выполнении определенных условий, которые зависят от значений и переменных в задаче. Поэтому, перед применением свойств, нужно внимательно анализировать задачу и убедиться, что они подходят для ее решения.
Логарифмы — это мощный математический инструмент, который упрощает решение задач и нахождение значений. Зная основные свойства логарифмов, мы можем с легкостью упрощать выражения и находить решения. Практика и углубленное знание этих свойств помогут вам стать уверенными в решении любых задач, связанных с логарифмами.
Способы решения логарифмических уравнений
Свойства логарифмов
Перед тем как перейти к методам решения уравнений, стоит вспомнить основные свойства логарифмов. Некоторые из них вам наверняка знакомы: логарифм произведения равен сумме логарифмов, логарифма частного — разности логарифмов, логарифм степени — произведению логарифма на показатель степени и т.д. Эти свойства помогут нам в дальнейшем в решении уравнений.
Метод замены переменной

Один из самых простых способов решить логарифмическое уравнение — это применить метод замены переменной. Для этого выбирается новая переменная, которая заменяет исходную в уравнении. Часто используется замена переменной вида u = logb(x) или v = logb(y), где b — основание логарифма.
После замены переменной уравнение преобразуется в алгебраическое уравнение, которое можно решить с помощью известных методов. Полученное решение подставляется обратно в исходное уравнение, чтобы проверить его корректность.
Метод логарифмирования
Другой распространенный метод решения логарифмических уравнений — это метод логарифмирования. Суть его заключается в применении логарифма к обеим сторонам уравнения. Это позволяет упростить уравнение, переводя его в эквивалентную форму, которую можно решить.
Важно помнить, что на практике необходимо проверить полученное решение, так как некоторые значения могут быть недопустимыми из-за ограничений логарифма.
Графический метод
Если у вас есть возможность построить график функции, которая содержит логарифмическое уравнение, то вы можете использовать графический метод для его решения. На графике вы найдете точки пересечения кривой с осью абсцисс, которые будут являться решениями уравнения.
Графический метод особенно полезен, когда решение уравнения невозможно найти аналитически и требует численных методов.
Метод применения свойств логарифмов
Продвинутый метод решения логарифмических уравнений заключается в использовании свойств логарифмов для объединения нескольких логарифмов в один. Затем, используя свойства экспоненты, уравнение переписывается в виде экспоненциального уравнения и решается таким образом.
Иногда для решения сложных логарифмических уравнений требуется комбинировать различные методы и свойства, чтобы получить окончательное решение.
Независимо от метода, который вы выберете для решения логарифмического уравнения, важно помнить о проверке полученного решения и записи ответа в правильной форме. Логарифмические уравнения могут иметь несколько решений или быть неразрешимыми, поэтому внимательность и аккуратность играют важную роль при решении таких задач.
Логарифмы в математических приложениях
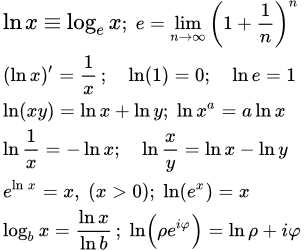
Одним из применений логарифмов является масштабирование данных. Во многих случаях данные имеют очень большие или очень малые значения, что затрудняет их анализ. Логарифмическое преобразование позволяет уравновесить разницу между этими значениями, делая их более удобными для работы. Например, в физике, когда измеряются электрические сопротивления, они могут варьироваться от микроом до мегаом. Применение логарифмической шкалы позволяет эффективно представить и анализировать эти значения.
Логарифмы также находят применение в решении сложных уравнений и вычислении экспоненциальных функций. Они позволяют преобразовывать сложные уравнения в более простые и легче решаемые формы. Например, логарифмическое дифференцирование может упростить задачи оптимизации и поиска экстремумов.
Кроме того, логарифмы применяются в экономике и финансовой математике для расчета процентных ставок, роста и дисконтирования денежных потоков. Они позволяют нам лучше понять временную стоимость денег и принимать обоснованные финансовые решения.
Инженеры также используют логарифмы для проектирования и анализа сложных систем. Например, в электротехнике, логарифмы используются для расчета амплитуды и фазы сигналов. Они также применяются в компьютерной графике для управления яркостью и цветом изображений.
Наконец, логарифмы широко применяются в научных исследованиях для анализа и интерпретации экспериментальных данных. Они позволяют установить связь между различными переменными и описать законы и закономерности, которые способствуют развитию науки.
Логарифмы: определение и способы решения
Основной логарифм – это логарифм с основанием 10. Обозначается он как log или lg.
Существуют несколько способов решения логарифмических уравнений. Наиболее распространенные из них:
- Использование свойств логарифмов. Свойства логарифмов позволяют переписывать логарифмические выражения в других формах, что упрощает и ускоряет решение уравнений. Некоторые из этих свойств:
- logb(xy) = logb(x) + logb(y)
- logb(x/y) = logb(x) — logb(y)
- logb(xn) = n * logb(x)
- logb(bn) = n
- Применение формулы изменения основания логарифма. Формула позволяет перевести логарифм с одним основанием в логарифм с другим основанием:
- Использование таблиц логарифмов. В прошлом, когда вычисления выполняли вручную, широко использовались таблицы логарифмов. С их помощью легче было находить значения логарифмов для заданных чисел. Сейчас такие таблицы стали менее популярными благодаря тому, что большинству людей доступны электронные вычислительные устройства.
logb(n) = loga(n) / loga(b)
Знание логарифмических свойств и умение применять их, а также умение работать с формулами и таблицами логарифмов, позволяют эффективно решать задачи, связанные с логарифмами.