Когда мы начинаем свои путешествия или решаем проблемы, в нашей жизни всегда присутствует одна важная величина – начальная координата. Это понятие имеет не только физический смысл, но и является символом развития и изменений. Начальная координата – это систематический подход к достижению своих целей. Она помогает нам определить место, с которого мы начинаем, и создает план действий на основе этого. В жизни каждого из нас начальная координата может быть разной – это может быть физическое расстояние, текущая ситуация или просто наша исходная точка. Но важно помнить, что начальная координата – это не только точка старта, но и возможность для роста и преодоления себя.
Понятие «начальная координата»
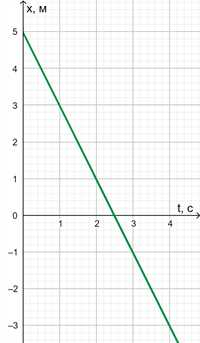
Для лучшего понимания понятия «начальная координата», давайте представим, что мы отправляемся в путешествие. Вначале нашего путешествия у нас есть точка, от которой мы начинаем свой путь. Это и есть наша начальная координата. Отсюда мы начинаем двигаться и отсчитывать расстояния до следующих точек нашего путешествия. Наша начальная координата является исходной точкой, относительно которой мы определяем наше местоположение и путь.
Подобным образом, в математике и физике, начальная координата используется для определения положения объекта в пространстве или на плоскости. Например, при изучении движения тела, начальная координата относится к точке, где тело начинает свое движение. Отсчитывая расстояния или изменения положения относительно начальной координаты, мы можем определить конечное положение объекта.
В геометрии начальная координата используется для определения точек на плоскости или в трехмерном пространстве. Например, в системе координат (x, y), начальная координата обычно выбирается в центре плоскости. От этой точки отсчитываются значения по осям x и y для определения положения любой другой точки.
Итак, начальная координата играет важную роль в измерении и определении положения объектов. Она является отправной точкой, от которой отсчитываются изменения положения. Понимание этого понятия помогает нам более точно определить и представить положение объектов в пространстве или на плоскости.
Значение начальной координаты в математике

Представьте себе безымянную точку на белом листе бумаги. Чтобы определить ее положение, мы устанавливаем начальную координату. Начальная координата обычно выбирается в левом нижнем углу плоскости и обозначается точкой (0,0). Взяв эту точку за начало системы координат, мы можем определить положение любого другого объекта на плоскости, используя два взаимно перпендикулярных направления — ось X и ось Y.
Значение начальной координаты в математике заключается не только в определении положения объектов, но и в решении простых и сложных математических задач. Представьте, что вам дано время и скорость движения объекта. Вы можете использовать начальную координату, чтобы рассчитать его местоположение в определенный момент времени с помощью формулы движения.
Начальная координата также важна в геометрии и алгебре. Она облегчает определение расстояний между точками, строительство графиков и графическую интерпретацию математических функций. Благодаря начальной координате мы можем составлять уравнения прямых, плоскостей и кривых в двухмерном пространстве.
Значение начальной координаты в математике состоит не только в том, чтобы помочь нам определить положение и решить математические задачи. Оно открывает нам двери в невероятно широкий мир математики, где мы можем исследовать законы природы, моделировать реальные ситуации и находить пути решения различных проблем. Начальная координата — это фундамент, на котором строится весь комплексный математический аппарат, и без нее мы не смогли бы достичь таких высот в науке и технологии.
Значение начальной координаты в физике
Ты когда-нибудь задумывался о том, откуда начинаются все наши движения и путешествия? В физике существует понятие начальной координаты, которое играет важную роль в определении движения и местоположения объектов.
Начальная координата — это точка, с которой начинается движение или положение объекта в пространстве. Она может быть определена в разных относительных системах координат, но в любом случае она является отправной точкой для измерения перемещений и местоположений.
Значение начальной координаты может быть положительным, отрицательным или нулевым, в зависимости от выбранной системы координат и положения объекта. Например, если выбрать систему координат, где начальная точка — это середина дороги, то положение объекта слева от середины будет иметь отрицательную координату, а справа — положительную. Также можно выбрать другую систему координат, где начальная точка — это одно из крайних значений, и тогда положение объекта будет определяться как положительной или отрицательной разницей от этой точки.
Значение начальной координаты позволяет нам отслеживать перемещения объектов в пространстве и анализировать их движение. Оно является отправной точкой для вычислений и рассчетов, связанных с физическими явлениями.
Представь, что ты заполнил свой автомобиль топливом и готов отправиться в путешествие. Но чтобы рассчитать расстояние, которое ты пройдешь, тебе нужно знать начальную координату — точку, откуда ты начинаешь свое путешествие. Без этой информации ты не сможешь рассчитать точное расстояние и не сможешь составить план своего маршрута.
Интересно, не правда ли? Мы постоянно используем понятие начальной координаты в нашей повседневной жизни, даже не задумываясь о том, как оно важно и полезно для нас. Оно помогает нам ориентироваться в пространстве и анализировать движение объектов.
Так что, следующий раз, когда ты будешь отправляться в путешествие или рассчитывать расстояние между двумя точками, помни о значении начальной координаты. Она поможет тебе определить свое местоположение и построить наилучший маршрут.
Значение начальной координаты в программировании
Давайте рассмотрим пример. Представьте, что вы разрабатываете компьютерную игру, в которой главный герой должен пройти через лабиринт. Каждый элемент в этом лабиринте имеет свои координаты — это его положение на оси X и Y. Начальная координата будет указывать, откуда главный герой начинает свой путь. Она помогает программе определить, какие действия необходимо выполнить для движения главного героя по лабиринту и отслеживает его текущую позицию в каждый момент времени.
Другой пример использования начальной координаты — это отслеживание движения объекта. Представьте, что у вас есть автомобиль, который движется по заданному маршруту. Начальная координата указывает, с какого места стартует автомобиль. Затем, используя различные алгоритмы и формулы, вы можете рассчитать новое положение автомобиля в каждый момент времени, используя его начальную координату и данные о скорости и направлении движения.
Очевидно, что без начальной координаты решение таких задач было бы невозможным. Она является отправной точкой для определения дальнейших действий и помогает программе ориентироваться в пространстве, отслеживать объекты и контролировать их движение.
Начальная координата: понятие и значения
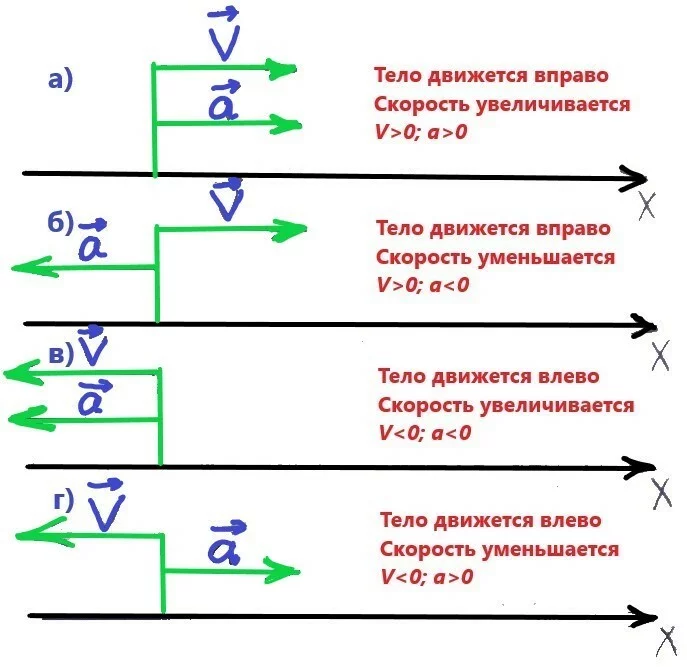
Значение начальной координаты может быть задано в различных системах координат. Например, в декартовой системе координат начальная координата представляет собой пару чисел (x, y), где x — горизонтальная координата, а y — вертикальная координата. В полярной системе координат начальная координата может быть задана радиусом r и углом φ.
В значительной части физических задач начальная координата играет важную роль. Она позволяет определить местоположение объекта в начальный момент времени и рассчитать его движение в дальнейшем. Начальная координата может быть измеряемой величиной, например, при измерении расстояния отсчет может начинаться от определенной точки. В некоторых случаях начальная координата может быть произвольным выбором, и она необходима для удобства исследования объекта или системы.
Примеры значений начальной координаты:
- Декартова система координат: (0, 0) — начало координат;
- Декартова система координат: (5, -2) — точка с горизонтальной координатой 5 и вертикальной координатой -2;
- Полярная система координат: (3, π/4) — точка с радиусом 3 и углом 45 градусов;
- Произвольная система координат, где начальная координата выбрана в произвольной точке.