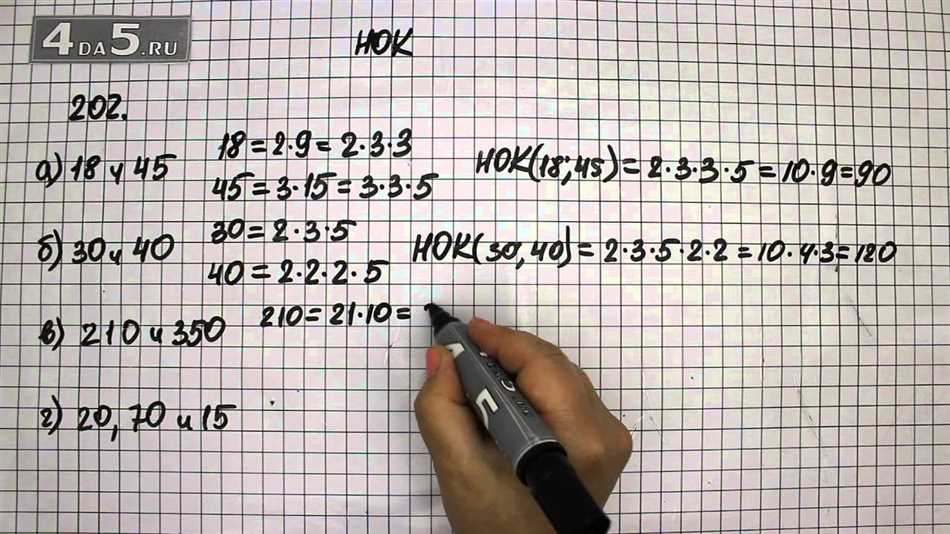
Когда мы изучаем математику, нам часто встречается понятие наименьшего общего кратного (НОК). Это очень важный термин, который помогает нам находить общие множители чисел. Несмотря на сложность этого понятия, в 6 классе мы уже начинаем изучать его с помощью учебника Виленкина. В этом уроке мы разберемся, как находить НОК двух или более чисел и как применять это знание на практике. Будем активно использовать примеры из жизни и решать интересные задачи, чтобы улучшить наши математические навыки. Присоединяйтесь и начнем наше путешествие в мир наименьшего общего кратного!
- Определение наименьшего общего кратного
- Что такое общее кратное?
- Что такое наименьшее общее кратное?
- Как найти наименьшее общее кратное двух чисел?
- Примеры вычисления наименьшего общего кратного
- Наименьшее общее кратное чисел в математике 6 класса ВиленкинаНаименьшим общим кратным (НОК) двух или более чисел называется наименьшее число, которое без остатка делится на каждое из данных чисел.Для нахождения НОК двух чисел следует применять алгоритм Евклида: Делаем разложение чисел на простые множители. Для каждого разложения записываем множители в обоих числах с наибольшими степенями. Произведение записанных в обоих числах множителей даст НОК. Пример: Найти НОК чисел 6 и 8. Разложим числа на простые множители: 6 = 2 * 3 8 = 2 * 2 * 2 Запишем наибольшие степени множителей: 6 = 2 * 3 * 1 8 = 2 * 2 * 2 Умножим записанные множители чисел: НОК = 2 * 3 * 2 * 2 = 24 Таким образом, НОК чисел 6 и 8 равно 24.
- Наименьшим общим кратным (НОК) двух или более чисел называется наименьшее число, которое без остатка делится на каждое из данных чисел.Для нахождения НОК двух чисел следует применять алгоритм Евклида: Делаем разложение чисел на простые множители. Для каждого разложения записываем множители в обоих числах с наибольшими степенями. Произведение записанных в обоих числах множителей даст НОК. Пример: Найти НОК чисел 6 и 8. Разложим числа на простые множители: 6 = 2 * 3 8 = 2 * 2 * 2 Запишем наибольшие степени множителей: 6 = 2 * 3 * 1 8 = 2 * 2 * 2 Умножим записанные множители чисел: НОК = 2 * 3 * 2 * 2 = 24 Таким образом, НОК чисел 6 и 8 равно 24.
Определение наименьшего общего кратного
Какой смысл этому определению? Давай разберемся.
Представь, что у тебя есть несколько чисел, например, 12, 18 и 24. И ты хочешь найти наименьшее число, которое делится на все эти числа без остатка. Для этого необходимо сначала выяснить, какие числа делятся на каждое из них без остатка. В данном примере, мы можем заметить, что 12 и 24 делятся на 12 без остатка, а 18 на 9 без остатка.
Теперь мы должны определить, какое наименьшее число делится на все эти числа без остатка. Здесь нам поможет понятие НОК. Мы можем увидеть, что НОК чисел 12, 18 и 24 равен 72. Это наименьшее число, которое делится на каждое из этих чисел без остатка.
Интересно, правда? НОК можно применить во множестве задач, например, для решения уравнений, сравнения дробей и т.е. Он позволяет нам понять, какое наименьшее число нам нужно найти для определенной ситуации.
Так что, не бойся математики! Наименьшее общее кратное — это понятие, которое поможет тебе решить различные задачи и понять, какие числа связаны между собой.
Что такое общее кратное?

Общие кратные часто используются, когда мы хотим найти наименьшее общее кратное (НОК) двух или более чисел. НОК — это наименьшее положительное число, которое делится на все данные числа без остатка.
НОК необходим, например, для упрощения работы с дробями. Когда мы складываем или вычитаем дроби с разными знаменателями, нам необходимо привести их к общему знаменателю. В этом случае наименьшее общее кратное знаменателей становится нашим общим знаменателем, что упрощает работу с дробями.
Как найти НОК двух чисел? Мы можем использовать метод факторизации — разложение чисел на простые множители:
- Для начала разложим числа на простые множители. Например, число 4 разлагается на простые множители как 2 * 2, а число 6 — как 2 * 3.
- Далее, возьмем каждый из простых множителей с наибольшей степенью. В данном примере у нас есть два раза число 2 и один раз число 3.
- Умножим эти множители: 2 * 2 * 3 = 12. Полученное число 12 будет наименьшим общим кратным чисел 4 и 6.
Итак, общее кратное — это число, которое делится на два или более числа без остатка, а наименьшее общее кратное (НОК) — это наименьшее положительное число, которое делится на все данные числа без остатка. НОК может быть найден с использованием метода факторизации, разложения чисел на простые множители и выбора множителей с наибольшей степенью.
Что такое наименьшее общее кратное?

Представьте себе, что у вас есть два числа: 4 и 6. Все числа, которые делятся и на 4, и на 6, являются их общими кратными. Некоторыми из таких чисел могут быть 12, 24, 36 и так далее. НОК этих двух чисел будет самым маленьким числом из всех таких общих кратных, то есть 12.
Наименьшее общее кратное можно найти разными способами. Один из самых простых способов — это разложить заданные числа на простые множители и затем составить наименьшее число, которое включает в себя все эти множители. Например, чтобы найти НОК чисел 4 и 6, мы разлагаем их на множители: 4 = 2 × 2, 6 = 2 × 3. НОК будет равно 2 × 2 × 3 = 12.
Зачем нам нужно вычислять НОК? Ответ прост: это помогает нам решать различные задачи и проблемы. Например, НОК используется для сравнения дробей с разными знаменателями. Или же для определения периода повторения десятичной дроби. Кроме того, НОК позволяет нам упрощать математические выражения и решать уравнения.
Теперь, когда вы знаете, что такое наименьшее общее кратное, вы можете легко применять этот концепт в своих школьных заданиях и решать разнообразные математические задачи без проблем. Уверен, что вам это точно пригодится!
Как найти наименьшее общее кратное двух чисел?

Для того чтобы найти НОК двух чисел, сначала нужно разложить их на простые множители. Простые множители — это числа, которые делятся только на себя и на единицу. Затем, необходимо выбрать все простые множители, которые встречаются в каждом из чисел, и умножить их друг на друга с учетом их степеней.
Например, найдем НОК чисел 12 и 18. Разложим их на простые множители:
- 12 = 2 * 2 * 3
- 18 = 2 * 3 * 3
Видим, что простые множители, встречающиеся в обоих числах, это 2 и 3. Учитывая их степени, мы получаем:
| Простой множитель | Степень в числе 12 | Степень в числе 18 |
|---|---|---|
| 2 | 2 | 1 |
| 3 | 1 | 2 |
Теперь умножим простые множители с их степенями:
2^2 * 3^1 * 3^2 = 4 * 3 * 9 = 36
Таким образом, НОК чисел 12 и 18 равен 36. Это наименьшее число, которое делится и на 12, и на 18 без остатка.
Использование НОК может быть полезным во многих задачах, например, при сравнении размеров долей или при работе с дробями. Понимание того, как найти НОК двух чисел, поможет вам лучше разобраться в этих темах и решать разнообразные задачи.
Примеры вычисления наименьшего общего кратного
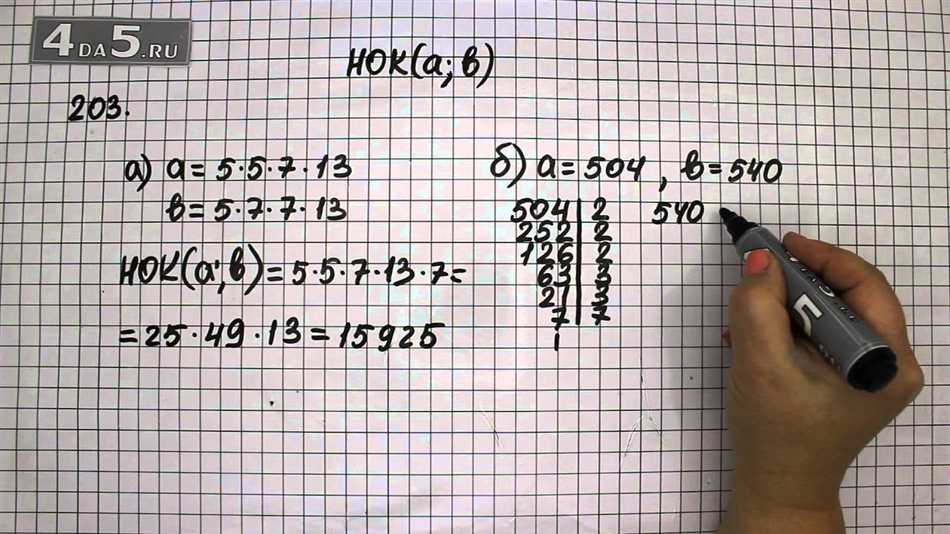
Пример 1:
Предположим, что нам нужно найти НОК чисел 4 и 6.
1. Мы можем начать с перечисления кратных чисел для каждого числа:
- Кратные числа для 4: 4, 8, 12, 16, 20,…
- Кратные числа для 6: 6, 12, 18, 24, 30,…
2. Затем мы можем найти наименьшее общее число, которое встречается в обоих списках — это число 12. Таким образом, НОК чисел 4 и 6 равно 12.
Пример 2:
Предположим, что нам нужно найти НОК чисел 3, 5 и 8.
1. Мы можем начать с перечисления кратных чисел для каждого числа:
- Кратные числа для 3: 3, 6, 9, 12, 15,…
- Кратные числа для 5: 5, 10, 15, 20, 25,…
- Кратные числа для 8: 8, 16, 24, 32, 40,…
2. Затем мы можем найти наименьшее общее число, которое встречается во всех трех списках — это число 120. Таким образом, НОК чисел 3, 5 и 8 равно 120.
Обратите внимание, что для того, чтобы найти НОК трех или более чисел, мы ищем наименьшее общее число, которое встречается во всех списках кратных чисел.
Пример 3:
Предположим, что нам нужно найти НОК чисел 9, 12 и 15.
1. Мы можем начать с перечисления кратных чисел для каждого числа:
- Кратные числа для 9: 9, 18, 27, 36, 45,…
- Кратные числа для 12: 12, 24, 36, 48, 60,…
- Кратные числа для 15: 15, 30, 45, 60, 75,…
2. Затем мы можем найти наименьшее общее число, которое встречается во всех трех списках — это число 180. Таким образом, НОК чисел 9, 12 и 15 равно 180.
Помимо перечисления кратных чисел, существуют и другие методы для вычисления НОК, такие как использование простых множителей или общей формулы. Но в основе всех этих методов лежит идея нахождения наименьшего общего числа, которое делится на все числа из данного набора.
Теперь, когда вы знаете несколько примеров вычисления наименьшего общего кратного, вы можете легко применять эти методы в своих задачах и упражнениях.
Наименьшее общее кратное чисел в математике 6 класса Виленкина
Наименьшим общим кратным (НОК) двух или более чисел называется наименьшее число, которое без остатка делится на каждое из данных чисел.Для нахождения НОК двух чисел следует применять алгоритм Евклида:
- Делаем разложение чисел на простые множители.
- Для каждого разложения записываем множители в обоих числах с наибольшими степенями.
- Произведение записанных в обоих числах множителей даст НОК.
Пример:
- Найти НОК чисел 6 и 8.
-
Разложим числа на простые множители:
6 = 2 * 3
8 = 2 * 2 * 2
-
Запишем наибольшие степени множителей:
6 = 2 * 3 * 1
8 = 2 * 2 * 2
-
Умножим записанные множители чисел:
НОК = 2 * 3 * 2 * 2 = 24
Таким образом, НОК чисел 6 и 8 равно 24.