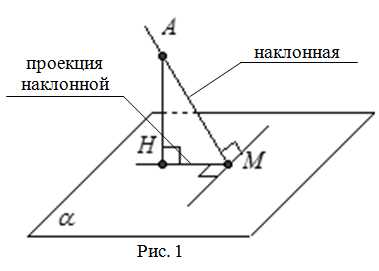
На уроках геометрии в 7 классе мы изучаем такое понятие, как наклонная. Наклонная – это прямая, которая не параллельна ни одной из сторон фигуры, но пересекает или проходит через её вершины. Отличить наклонную от других прямых поможет её направление и наклон. Наклонную можно найти в различных геометрических фигурах, таких как треугольники, прямоугольники, параллелограммы и т.д. Например, наклонные можно найти в равнобедренном треугольнике, где они проходят через вершины основания и угла.
Наклонная в геометрии 7 класс
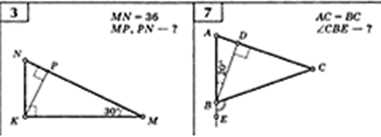
Наклонная – это отрезок, соединяющий вершину прямоугольного треугольника с точкой на противоположном катете, не являющейся концом. Такая точка на катете называется основанием наклонной.
Представим себе следующую ситуацию. У тебя есть прямоугольный треугольник со сторонами a, b и c, где стороны a и b – это катеты, а c – гипотенуза. И ты знаешь длину гипотенузы c и одного из катетов, например, a. Тебе нужно найти длину наклонной, которая соединяет вершину треугольника с основанием.
Так как наклонная является отрезком, мы можем использовать теорему Пифагора, чтобы найти ее длину. Теорема Pифагора гласит, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Теперь вернемся к нашей задаче. У нас есть катет a и гипотенуза c, и мы хотим найти наклонную. Используя теорему Пифагора, мы можем записать уравнение: c² = a² + b², где b – искомая длина наклонной.
Теперь давай решим эту задачу вместе. Предположим, что у нас есть прямоугольный треугольник со сторонами a = 3 и c = 5. Чтобы найти длину наклонной, мы можем подставить эти значения в уравнение: 5² = 3² + b². Решим это уравнение.
Для начала возведем в квадрат оба числа: 25 = 9 + b². Теперь вычтем 9 из 25: b² = 16. Наконец, извлечем квадратный корень из обеих сторон уравнения: b = 4. Значит, длина наклонной равна 4.
Наклонные имеют широкое применение в реальной жизни. Например, они используются при строительстве лестницы на склоне или при расчете высоты дерева с помощью прямоугольного треугольника.
Теперь, когда ты знаешь, что такое наклонная и как ее найти, ты можешь решать различные задачи, связанные с прямоугольными треугольниками. И не забывай применять теорему Пифагора, она очень полезна!
Определение
Когда мы говорим о наклонной, мы обычно представляем себе наклонную плоскость или линию. Например, когда видим склон в горах или крышу дома, мы видим наклонные поверхности. В геометрической терминологии наклонная часто является элементом более сложных форм, таких как треугольники, параллелограммы или параллелепипеды.
Наклонные имеют свои особенности и свойства, которые важны для понимания и решения задач. Например, угол наклона указывает на степень наклона поверхности или уклона линии. Чем больше угол, тем круче наклон. Коэффициент наклона используется для выражения отношения вертикального изменения к горизонтальному изменению на наклонной плоскости.
Наклонные могут иметь различные применения в разных областях, начиная от архитектуры и гражданского строительства до визуального искусства и дизайна. Знание основных понятий и примеров наклонной помогает понять и описать окружающий мир и использовать его в творческих или практических целях. В итоге, понимание наклонной дает нам возможность расширить наше знание о формах, фигурах и их взаимодействии в трехмерном пространстве.
Угол наклона
Ты наверняка замечал углы наклона в повседневной жизни. Например, крыши домов, скаты гор, лестницы, дороги с подъемами или спусками — все они имеют определенный угол наклона. Угол наклона часто исползуется в строительстве, географии, архитектуре и других областях.
Понимание угла наклона очень важно. Оно позволяет нам определить, насколько крутая или пологая поверхность, плоскость или наклонная прямая. Зная угол наклона, мы можем сделать предположения о том, насколько круто или полого будет подъем или спуск.
Для измерения угла наклона используется инструмент, называемый угломером или наклономером. Он позволяет точно определить угол наклона и использовать эту информацию для нужных расчетов и построений.
Углы наклона могут быть положительными или отрицательными в зависимости от того, как они направлены. Например, если угол направлен вверх от горизонтальной линии, то он будет положительным. Если угол направлен вниз от горизонтальной линии, то он будет отрицательным.
Мы можем классифицировать углы наклона в зависимости от их величины. Малые углы наклона будут почти горизонтальными, а большие углы наклона будут почти вертикальными. Ты даже можешь сам посмотреть на окружающую тебя среду и попытаться определить некоторые углы наклона.
Это было краткое описание угла наклона. Он очень важный концепт в геометрии и ежедневной жизни, который помогает нам понять и описать различные наклонные прямые и поверхности. Надеюсь, что теперь ты лучше понимаешь, что такое угол наклона и как он используется в нашей жизни!
Примеры

Поговорим о наклонных линиях и их применении в жизни. Наклонная, это такая линия, которая не параллельна ни одной из осей (горизонтальной или вертикальной). Встречаются они часто в повседневной жизни.
Представь себе, что ты живешь в доме с двумя этажами. Ты можешь заметить, что лестница из первого этажа на второй наклонена. Вот и пример наклонной линии в доме! Обрати внимание, что наша лестница не параллельна ни горизонтальной, ни вертикальной оси. Ее угол наклона помогает нам подниматься на второй этаж. А затем мы спускаемся по ней вниз. Лестницы — это прекрасный пример наклонной линии, с которой ты сталкиваешься каждый день.
Еще один пример наклонной линии — это скат крыши. Если ты внимательно присмотришься к домам вокруг тебя, то заметишь, что большинство из них имеют скаты крыши. Для чего нам нужны эти скаты? Наклон крыши позволяет осадкам, таким как дождь или снег, стекать с крыши, а не задерживаться на ней. Это очень важно, чтобы избежать возможных протечек или повреждений крыши. Поэтому скаты крыши — это еще один пример использования наклонных линий в повседневной жизни.
А ты замечал наклонные линии в других местах? Может быть, на дорогах, где используются пандусы для колясок и инвалидных кресел? Или в парке, где наклонные дорожки помогают людям идти под углом?
Наклонные линии не только функциональны, но и могут быть интересными и красивыми в дизайне. Например, в архитектуре и искусстве часто используется наклонные линии, чтобы создать ощущение движения или динамики. Такие линии могут быть замечены в зданиях, мостах, скульптурах и других произведениях искусства.
Так что следующий раз, когда увидишь наклонную линию в жизни, подумай о том, как она помогает нам и в каких сферах еще может быть использована. Наклонные линии — это не только геометрическое понятие, но и часть нашей повседневной жизни!
Наклонная в геометрии 7 класс – основные понятия и примеры
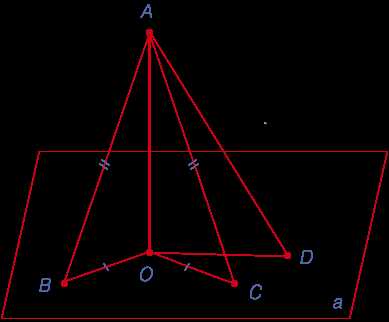
Наклонная обозначается символом «/». Если наклонная идет вправо, то она направлена вверх и влево. Если наклонная идет влево, то она направлена вверх и вправо.
Примеры наклонных:
- Наклонная вправо:
| Линия | Наклон |
|---|---|
| / | Наклон вверх и влево |
| | | Вертикальная линия |
| \ | Наклон вниз и влево |
- Наклонная влево:
| Линия | Наклон |
|---|---|
| \ | Наклон вверх и вправо |
| | | Вертикальная линия |
| / | Наклон вниз и вправо |