Геометрия – это наука, которая изучает формы, размеры, взаимное расположение и свойства пространственных объектов. Одним из основных понятий, используемых в геометрии, является угол. Углы могут иметь различные характеристики, в зависимости от их положения, и одним из таких свойств являются накрест лежащие углы.
Накрест лежащие углы – это два угла, расположенных на прямых линиях и пересекающихся таким образом, что одна пара противоположных углов образуется. Накрест лежащие углы часто встречаются в различных геометрических конструкциях и имеют несколько основных свойств, которые важно понимать и учитывать при решении геометрических задач. В данной статье мы рассмотрим определение и основные свойства накрест лежащих углов в геометрии.
- Определение накрест лежащих углов
- Основные свойства накрест лежащих углов
- Свойство 1: Равенство накрест лежащих углов
- Свойство 2: Углы, формируемые накрест лежащими углами
- Свойство 3: Углы, дополнительные к накрест лежащим углам
- Свойство 4: Параллельные прямые и накрест лежащие углы
- Внешние и внутренние накрест лежащие углы
- Внешние накрест лежащие углы
- Внутренние накрест лежащие углы
- Сумма внутренних и внешних накрест лежащих углов
- Равенство внешних и внутренних накрест лежащих углов
- Параллельные линии и накрест лежащие углы
- Накрест лежащие углы в геометрии: определение и основные свойства
Определение накрест лежащих углов
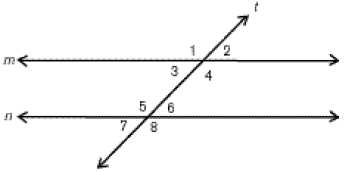
Чтобы лучше понять, что такое накрест лежащие углы, представь себе две прямые, пересекающиеся друг с другом. Когда прямые пересекаются, они образуют четыре угла — два смежных и два накрест лежащих.
Накрест лежащие углы обозначаются буквами и маленькими дугами, которые отмечают их стороны. Например, накрест лежащие углы могут быть обозначены как ∠a и ∠c, где ∠a и ∠c — это накрест лежащие углы относительно прямых a и c.
Накрест лежащие углы имеют несколько важных свойств, которые могут помочь в их дальнейшем анализе и использовании в геометрии. Вот некоторые из основных свойств накрест лежащих углов:
- Сумма углов: Сумма двух накрест лежащих углов всегда равна 180 градусов. Если ∠a и ∠c образуют пару накрест лежащих углов, то ∠a + ∠c = 180°.
- Углы вертикальные: Накрест лежащие углы также являются вертикальными углами. Это означает, что они равны друг другу. Если ∠a соответствует ∠d, а ∠c соответствует ∠b, то ∠a = ∠d и ∠c = ∠b.
- Заменяемость: Накрест лежащие углы могут быть заменены другими углами, которые имеют те же меры. Например, если ∠a = 60°, то его можно заменить другим углом, таким как ∠d = 60°.
Теперь, когда мы знаем определение и основные свойства накрест лежащих углов, давайте рассмотрим примеры и попрактикуемся в их использовании. Задумайся, где еще можно встретить накрест лежащие углы в повседневной жизни и как их свойства могут быть полезны для решения различных задач?
Основные свойства накрест лежащих углов
Свойство 1: Равенство накрест лежащих углов
Одно из основных свойств накрест лежащих углов заключается в том, что они равны. Если две прямые пересекаются, то углы, образованные этой пересекающей прямой и двумя параллельными прямыми, называются накрест лежащими. Эти углы всегда равны между собой. Например, если угол 1 и угол 2 — накрест лежащие углы, то угол 1 равен углу 2.
Свойство 2: Углы, формируемые накрест лежащими углами
Еще одно интересное свойство накрест лежащих углов заключается в том, что они образуют пары углов, которые в сумме дают 180 градусов. Если мы взглянем на прямую, пересекающую две параллельные прямые, то увидим, что сумма углов 1 и 2 равна 180 градусам. То же самое можно сказать и о углах 3 и 4, углах 5 и 6 и так далее. Действительно, каждая пара накрест лежащих углов в сумме дает 180 градусов. Это интересное свойство можно проверить самостоятельно с помощью геометрической модели или просто нарисовав прямые и углы на бумаге.
Свойство 3: Углы, дополнительные к накрест лежащим углам
Еще одно свойство накрест лежащих углов — это то, что углы, дополнительные к ним, также равны между собой. Углы, дополнительные к накрест лежащим углам, образуются прямой, которая пересекает две параллельные прямые. Если угол 1 и угол 3 — накрест лежащие углы, то угол 3 равен углу 5. То же самое можно сказать и о углах 2 и 4, углах 4 и 6 и так далее. Действительно, каждая пара дополнительных углов, образованных прямой, пересекающей две параллельные прямые, равна между собой.
Свойство 4: Параллельные прямые и накрест лежащие углы
Вот и все основные свойства накрест лежащих углов. Они могут показаться сложными на первый взгляд, но на самом деле легко запоминаются и применяются в геометрии. Надеюсь, эти свойства помогут вам разобраться с накрест лежащими углами и сделать ваше путешествие в мир геометрии более интересным и увлекательным!
Внешние и внутренние накрест лежащие углы
В геометрии накрест лежащими углами называются пары углов, размещенных по разные стороны от пересекающихся прямых, но находящихся на одной стороне друг от друга. В зависимости от того, расположены ли они снаружи или внутри пересеченных прямых, накрест лежащие углы могут быть внешними или внутренними.
Внешние накрест лежащие углы
Внешние накрест лежащие углы образуются двумя прямыми, пересекающими третью прямую. Они находятся по разные стороны от пересекающихся прямых, но за пределами их пересечения. Внешние накрест лежащие углы имеют общую вершину и общую сторону, которые являются продолжениями стороны одного угла и стороны другого. Их значения равны и сумма измерений двух внешних накрест лежащих углов составляет 180 градусов.
Например, если две прямые пересекают третью прямую, то угол 1 и угол 2 будут внешними накрест лежащими углами:
| Прямая AB | Прямая CD | |||
| ↓ | ↓ | |||
| А | В | С | D | |
| ↖ | ↖ | |||
| 1 | 2 | |||
Внутренние накрест лежащие углы

Внутренние накрест лежащие углы образуются двумя прямыми, пересекающими третью прямую. Они находятся по разные стороны от пересекающихся прямых, но внутри их пересечения. Внутренние накрест лежащие углы также имеют общую вершину и общую сторону, которые являются продолжениями стороны одного угла и стороны другого. Внутренние накрест лежащие углы в сумме дают 180 градусов.
Например, если две прямые пересекают третью прямую, то угол 3 и угол 4 будут внутренними накрест лежащими углами:
| Прямая EF | Прямая GH | |||
| ↓ | ↓ | |||
| Е | F | G | H | |
| ↙ | ↙ | |||
| 3 | 4 | |||
Внешние и внутренние накрест лежащие углы – это важное понятие в геометрии, и они применяются для решения различных задач. Понимание и использование этих углов поможет вам лучше понять пространственные отношения и свойства фигур, а также решать различные геометрические проблемы.
Сумма внутренних и внешних накрест лежащих углов
Итак, сумма внутренних и внешних накрест лежащих углов имеет определенные свойства. Пусть у нас есть две прямые, пересекающиеся между собой. Тогда сумма внутренних накрест лежащих углов равна 180 градусам. Это означает, что если мы измерим углы по отдельности и просуммируем их, полученный результат будет равен 180 градусам.
С другой стороны, сумма внешних накрест лежащих углов тоже равна 180 градусам. Это означает, что если мы измерим каждый угол отдельно, а затем просуммируем их, мы также получим 180 градусов. Главное отличие заключается в том, что внешние углы расположены сразу на противоположных сторонах прямых, в отличие от внутренних углов.
Накрест лежащие углы широко применяются в геометрии и имеют много практических применений. Например, они используются при решении задач на построение графиков, расчетов углов поворота и многих других геометрических проблем.
Учитывая все вышеупомянутые свойства накрест лежащих углов, мы можем легко выполнять вычисления и строить точные геометрические модели на основе этих углов. Понимание и применение этих свойств помогает нам улучшить наши навыки геометрии и решать сложные задачи с большей уверенностью и точностью.
Равенство внешних и внутренних накрест лежащих углов
Удивительным свойством накрест лежащих углов является их равенство. Внутренний и внешний накрест лежащие углы, образованные с одной и той же парой прямых, равны между собой. Это означает, что если мы знаем один из внутренних накрест лежащих углов, мы можем найти значение другого угла.
Зачастую мы сталкиваемся с ситуациями, когда нам необходимо найти отсутствующий угол в геометрической фигуре. В таких случаях знание равенства внутренних и внешних накрест лежащих углов может нам очень помочь.
Допустим, у нас есть две пересекающиеся прямые, и нам нужно найти угол A. Мы знаем, что внутренний накрест лежащий угол B равен 60 градусов. Тогда, согласно свойству равенства, внешний накрест лежащий угол C также равен 60 градусов. Итак, мы нашли отсутствующий угол A.
Пример:

Таким образом, равенство внешних и внутренних накрест лежащих углов — это важное свойство, которое можно использовать для решения геометрических задач. Накрест лежащие углы встречаются не только в геометрии, но и в различных других областях, таких как физика, инженерия и архитектура.
Теперь, когда у вас есть понимание равенства внутренних и внешних накрест лежащих углов, вы можете применять это знание для решения задач и демонстрации общих закономерностей в геометрии.
Параллельные линии и накрест лежащие углы
Представьте себе две параллельные линии, их пути никогда не пересекаются. Но что происходит, когда к ним приходит третья перпендикулярная линия? Возникают накрест лежащие углы!
Накрест лежащие углы — это две пары углов, образованных пересекающимися и перпендикулярными линиями. Они находятся по разные стороны от пересекающей линии и имеют общую вершину.
Интересно, какие свойства у этих углов?
Во-вторых, накрест лежащие углы являются дополнительными друг к другу. Это означает, что сумма мер этих углов равна 180 градусам. Например, если один угол равен 70 градусам, то другой угол будет равен 110 градусам.
Накрест лежащие углы находят применение во многих аспектах жизни. Например, они используются в архитектуре для построения параллельных стен и углов. Также они помогают в различных ситуациях в геометрии, физике и инженерии, где точные измерения и расчеты играют важную роль.
Теперь представьте, что вы стали мастером в использовании накрест лежащих углов. Какие возможности открываются перед вами? Вы сможете с легкостью решать задачи и находить правильные решения. Вы сможете видеть скрытые связи и закономерности в геометрии и других областях, где применяется этот концепт.
Итак, не смотря на свою простоту, накрест лежащие углы играют важную роль в геометрии и других дисциплинах. Они помогают нам делать точные измерения, анализировать структуру и взаимосвязь объектов, и, конечно же, позволяют нам расширить наши знания и умения.
Накрест лежащие углы в геометрии: определение и основные свойства
Основные свойства накрест лежащих углов:
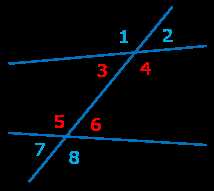
- Накрест лежащие углы равны между собой. Это означает, что если две прямые линии пересекаются и образуют накрест лежащие углы, то эти углы будут иметь одинаковую величину. Например, угол 1 будет равен углу 3, а угол 2 будет равен углу 4.
- Сумма накрест лежащих углов составляет 180 градусов. Если задача предполагает, что накрест лежащие углы образуются параллельными прямыми, то их сумма будет равна 180 градусов. Например, если угол 1 равен 60 градусам, то угол 2 будет равен 120 градусам.
- Накрест лежащие углы дополнительны друг другу. Это означает, что если сумма накрест лежащих углов составляет 180 градусов, то они являются дополнительными друг другу. Например, если угол 1 равен 60 градусам, то его дополнительный угол 3 будет равен 120 градусам.
Данные свойства накрест лежащих углов могут быть использованы для решения задач, основанных на взаимодействии пересекающихся и параллельных прямых. Они также играют важную роль в доказательствах и применяются для нахождения неизвестных углов и сторон в геометрических фигурах.