Вы когда-нибудь задумывались о том, каким образом математики объединяют два числа или два предмета? Возможно, вам знаком термин «наложение», но что именно он означает и каким образом можно применить его в математике?
На самом деле, наложение является одним из основных принципов математики, который помогает объединять или суммировать различные объекты или идеи. Он может быть использован для решения простых арифметических примеров или более сложных математических задач.
Давайте погрузимся глубже в мир наложения и изучим, как его использовать в разных математических задачах. Вы будете удивлены, насколько эффективно и интересно может быть применение этого концепта в решении математических задач! Ведь математика не такая уж и сложная, правда?
Раздел 1: Что такое наложение в математике?
В основном, наложение — это термин, описывающий процесс сравнения двух или более геометрических фигур, чтобы определить, совпадают ли они или нет. Когда мы говорим о наложении, мы рассматриваем, можно ли совместить одну фигуру с другой без изменения размера или искажения формы.
Зачем нам нужно наложение в математике? Хороший вопрос! Наложение помогает нам определить, равны ли две фигуры или нет. Это может быть очень полезным при решении задач на геометрию и при доказательстве геометрических утверждений.
Есть несколько способов сравнить две фигуры при помощи наложения. Один из них — это наложение по контуру. Грубо говоря, мы берем одну фигуру и проверяем, может ли ее контур быть совмещен с контуром другой фигуры. Если контуры совпадают, значит, фигуры равны.
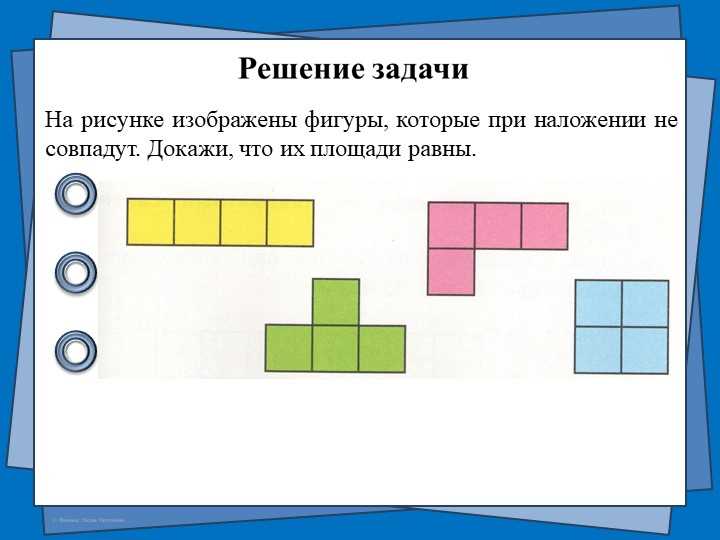
Другой способ наложения — это наложение по фигурам. Здесь мы берем две фигуры и проверяем, можно ли одну фигуру разделить на несколько частей, каждая из которых может быть совмещена с другой фигурой без изменения их размеров или форм.
Наложение — это не только полезный инструмент в математике, но и интересная игра. Попробуй сам сравнить несколько фигур и посмотреть, совпадают ли они или нет. Это поможет тебе развить свои навыки визуализации и логического мышления.
Итак, теперь ты знаешь, что такое наложение в математике. Готов попробовать сравнить несколько фигур и проверить, равны ли они? Уверен, ты справишься с этой задачей!
Определение понятия наложение

В математике наложение является важным понятием, которое помогает понять, какие части объектов пересекаются или совпадают друг с другом. Также наложение позволяет анализировать различные геометрические формы и определять их свойства.
Например, представьте себе два круга, расположенных один над другим. Если один круг полностью находится внутри другого, то мы можем сказать, что происходит наложение. Или представьте, что у вас есть два прямоугольника, и один из них частично перекрывает другой. В этом случае тоже происходит наложение.
Знание понятия наложения может быть полезным в различных областях жизни. Например, в архитектуре и дизайне наложение используется для создания эффектных композиций и интересных геометрических форм. В физике наложение позволяет моделировать перекрытие объектов и изучать их взаимодействие.
В заключении, понимание понятия наложения является важным элементом математики и геометрии. Оно позволяет анализировать перекрытие объектов и понимать, как они связаны друг с другом. Наложение также имеет практическое применение в различных областях и может быть использовано для создания уникальных и интересных решений.
Примеры наложения в математике
Пример 1: Наложение в прямоугольных треугольниках
Представьте себе два прямоугольных треугольника, смежные стороны которых совпадают. Возьмем один треугольник и наложим его на другой так, чтобы их смежные стороны точно совпадали. Если оба треугольника идентичны, то мы получим квадрат, так как все углы в этом случае будут прямыми.
Пример 2: Наложение в решении геометрических задач
Наложение применяется не только для решения геометрических задач, но и для построения различных форм и фигур. Например, если мы хотим построить правильный шестиугольник с помощью циркуля и линейки, мы можем начать с построения равностороннего треугольника и затем наложить такие же, но со сдвигом, чтобы получить шестиугольник.
Пример 3: Наложение во время изучения функций
Когда мы изучаем функции в математике, мы часто используем наложение, чтобы упростить их анализ и понимание. Если у нас есть две функции и мы хотим узнать, где они пересекаются или где происходят изменения, мы можем наложить графики этих функций и наглядно увидеть, где они сходятся или расходятся.
Таким образом, наложение играет важную роль в различных областях математики, начиная от геометрии и заканчивая анализом функций. Оно помогает нам визуализировать и понять сложные концепции, делая математику более доступной и увлекательной. Попробуйте сами применить наложение во время решения задач или изучения новых концепций – и вы увидите, как это поможет вам лучше понять математику
Раздел 2: Зачем нужно знать о наложении в математике?
Вы когда-нибудь задумывались, зачем нам нужно знать о наложении в математике? Может показаться, что это безразличная тема, которая не привносит ничего нового в нашу жизнь. Однако на самом деле знание о наложении имеет свою ценность и применение в реальном мире.
Давайте рассмотрим несколько причин, почему знание о наложении важно:
1. Развитие пространственного мышления
Столкнувшись с задачами на наложение, мы активно тренируем наше пространственное мышление. Образное и пространственное мышление позволяют нам воспринимать и понимать информацию, связанную с пространством и формой. Знание о наложении помогает нам лучше представлять себе, как два объекта или фигуры могут быть выровнены друг с другом.
2. Построение геометрических моделей
Геометрические модели являются важным инструментом для анализа и понимания различных объектов и процессов в мире. Знание о наложении помогает нам строить такие модели и использовать их для решения разных задач. Например, если мы должны построить мост или здание, знание о наложении поможет нам правильно расположить и выровнять конструкционные элементы.
3. Решение задач в реальном мире
Знание о наложении позволяет нам решать различные задачи в реальном мире. Например, если вы занимаетесь дизайном интерьеров, знание о наложении поможет вам правильно разместить и выровнять мебель и другие элементы интерьера. Если вы работаете в сфере строительства или архитектуры, знание об этой концепции позволит вам рассчитывать и строить составные узлы и детали.
Кроме того, знание о наложении может быть полезным при решении задач из других областей, таких как компьютерная графика, криптография и т.д.
Таким образом, знание о наложении в математике является ценным и полезным навыком, который можно применять в различных сферах жизни. Необходимо осознавать, что математика не ограничивается только школьными уроками, но имеет широкий спектр применений в реальной жизни. Умение применять знания о наложении не только улучшит ваш успех в учебе, но и поможет вам решать задачи и проблемы в повседневной жизни.
Применение наложения в реальной жизни

Концепция наложения — одна из таких математических техник, которая может быть использована во многих аспектах нашей жизни. Один из примеров применения наложения — это графический дизайн. Дизайнеры используют наложение для создания сложных и красивых изображений, комбинируя различные элементы и цвета. Они могут наложить одну картинку на другую, изменить прозрачность и настроить настройки смешивания цветов, чтобы создать желаемый эффект.
Наложение также находит свое применение в фотографии. С помощью наложения можно объединить несколько фотографий в одно изображение, создавая коллажи и композиции. Кроме того, фотографы могут использовать наложение, чтобы создать эффект двойного экспонирования, объединяя два разных снимка в одном.
Наложение играет важную роль в компьютерной графике и анимации. Графические программы используют наложение для создания реалистичных текстур и эффектов освещения. Аниматоры могут наложить несколько слоев изображений, чтобы создать плавные переходы и движение.
Не только в искусстве и дизайне наложение имеет применение. Оно используется в материалах строительства, чтобы создать прочные и устойчивые структуры. В медицине наложение используется для объединения и анализа различных областей изображений, полученных с помощью различных методов диагностики. В бизнесе наложение находит свое применение в анализе данных и прогнозировании.
Очень интересно, как множество областей жизни находят способы применения наложения. Это просто демонстрирует, насколько важно обладать хорошими навыками в математике и уметь применять их на практике. Так что не отрицайте ценность математики в реальной жизни!
Научитесь о наложении в математике
Для наложения двух фигур можно использовать различные методы. Один из наиболее простых и распространенных способов — это использование сетки. Сетка позволяет выравнивать фигуры и определять их соответствие друг другу.
Шаги для наложения фигур с использованием сетки:
- Нарисуйте сетку на листе бумаги или на графическом дисплее.
- Нарисуйте одну из фигур на сетке.
- Сместите сетку и нарисуйте вторую фигуру.
- Сравните две фигуры и определите, совпадают ли они или нет.
Важно помнить, что при наложении фигур необходимо учитывать масштаб и соответствие размеров. Также стоит обратить внимание на ориентацию и положение фигур относительно друг друга.
Наложение фигур широко применяется в области геометрии, при решении задач по нахождению площадей, периметров и других характеристик фигур. Оно также используется при изучении симметрии и преобразованиях фигур.