Натуральные логарифмы: основы и применение в математике и науке

Определение натурального логарифма

Логарифм — это математическая функция, которая описывает степень, в которую нужно возвести определенное число (основание логарифма), чтобы получить другое число. В простых словах, логарифм показывает, сколько раз нужно умножить основание на самого себя, чтобы получить заданное число.

Основание логарифма может быть любым положительным числом, но при определении натурального логарифма основание равно числу Эйлера, обозначаемому как «e». Число Эйлера — это особая иррациональная константа, которая равна приблизительно 2,71828.

Таким образом, натуральный логарифм числа «x» — это показатель степени, в которую нужно возвести число «e», чтобы получить значение «x». Он обозначается как «ln(x)».

Натуральный логарифм имеет некоторые уникальные свойства, которые делают его полезным в различных областях. Например, он возникает в процессе моделирования роста популяции и распределения вероятностей. Также его эффективно применяют в финансовой математике, экономике, физике и других дисциплинах.

Основное применение натурального логарифма — это вычисление сложных математических функций и приведение их к более простому виду. Он помогает сократить сложность вычислений и упростить анализ данных. Благодаря своей универсальности и гибкости, натуральный логарифм позволяет нам лучше понимать и описывать мир вокруг нас.

Отличия натуральных логарифмов от обычных

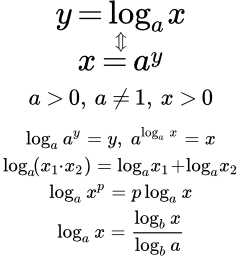
Одно из главных отличий между натуральными логарифмами и обычными — основание. Основание e придает натуральным логарифмам особую мощь и уникальные свойства. Есть особенный численный постоянный e, которое равно примерно 2,71828. Именно это число является основой натуральных логарифмов.

Одним из преимуществ натуральных логарифмов является их использование в различных областях науки и математики. Например, они широко применяются для моделирования экспоненциального роста или убывания, а также для решения уравнений с логарифмическими функциями. Также, натуральные логарифмы часто используются для измерения времени, популяций, анализа финансовых данных и в других приложениях.

Еще одной важной особенностью натуральных логарифмов является их связь с экспонентами. Функция экспоненты взаимно обратна функции натурального логарифма: если мы возведем число e в степень равную x, то получим экспоненту x. Эта взаимосвязь между экспонентой и натуральными логарифмами играет ключевую роль во многих математических и физических моделях.

Еще одна интересная особенность натуральных логарифмов заключается в их равноучастии во многих математических формулах и идентичностях. Например, известная идентичность e^πi + 1 = 0, называемая формулой Эйлера, связывает основные математические константы e, π и i, и демонстрирует глубину и красоту математических отношений, которые могут быть обнаружены с помощью натуральных логарифмов.

Итак, вот некоторые отличия натуральных логарифмов от обычных: использование основания e, широкое применение в науке и математике, связь с экспонентами и участие в важных идентичностях. Натуральные логарифмы — это мощный инструмент, который помогает нам понять мир вокруг нас и решать сложные математические задачи.

Математические свойства натуральных логарифмов

1. Свойство логарифма отношений

Одним из важных свойств натурального логарифма является его способность упростить сложение и вычитание между различными величинами. Когда мы применяем натуральный логарифм к отношению двух чисел, мы можем записать это в виде разности между натуральными логарифмами этих двух чисел. Например, натуральный логарифм отношения чисел a и b можно записать как ln(a/b) = ln(a) — ln(b).

Это свойство позволяет нам упростить вычисления и работать с различными значениями в более удобной форме.

2. Свойство логарифма степеней

Натуральные логарифмы также обладают свойством упрощения степеней. Когда мы применяем натуральный логарифм к числу, возведенному в степень, мы можем записать это в виде произведения между степенью и натуральным логарифмом исходного числа. Например, натуральный логарифм числа a, возведенного в степень b, можно записать как ln(a^b) = b * ln(a).

Это свойство упрощает вычисления и позволяет нам работать с большими степенями чисел более удобным способом.

3. Связь с экспонентой

Натуральные логарифмы и экспонента tесно связаны друг с другом. Важное математическое свойство состоит в том, что натуральный логарифм числа a равен степени экспоненты, которая равна этому числу, то есть ln(a) = e^x, где x — значение натурального логарифма.

Это свойство позволяет нам использовать натуральные логарифмы для обратного преобразования экспоненты и нахождения значения числа a по известному значению натурального логарифма.

4. Свойство натурального логарифма нуля и единицы

Натуральный логарифм числа 1 равен нулю, то есть ln(1) = 0. Это свойство очевидно, так как экспонента, возведенная в степень 0, всегда равна 1.

Натуральный логарифм числа 0 не имеет определенного значения, так как невозможно получить ноль путем возведения числа e в какую-либо степень. Это свойство отражает особенность работы натуральных логарифмов и делает его не применимым для нулевых значений.

Заключение

Натуральные логарифмы обладают различными математическими свойствами, которые позволяют упростить вычисления и работать с числами более удобным способом. С помощью свойств логарифма отношений, логарифма степеней и связи с экспонентой мы можем эффективно использовать натуральные логарифмы в различных областях науки, техники и финансов. Однако, необходимо помнить, что натуральные логарифмы не имеют определенного значения для нулевых чисел, что ограничивает их применимость в некоторых случаях.

График натурального логарифма

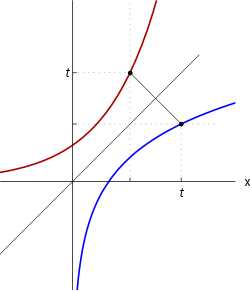
На графике натурального логарифма можно заметить несколько ключевых моментов. Во-первых, график всегда положительный, так как результат натурального логарифма всегда больше нуля. Это имеет смысл, если вспомнить, что экспонента, которая является основой натурального логарифма, всегда положительна.

Во-вторых, график имеет форму плавного возрастающего графика с постепенно уменьшающимся приростом. Сначала график растет быстро, с высоким наклоном, но с течением времени рост становится все медленнее, и наклон графика уменьшается. Это свойство объясняется тем, что натуральный логарифм логарифмирует экспоненциальный рост.

Также, график натурального логарифма проходит через точку (1, 0), что означает, что значение натурального логарифма от числа 1 равно 0. Это свойство позволяет использовать натуральный логарифм в различных математических и научных расчетах.

График натурального логарифма можно использовать для решения различных задач. Например, он может помочь в предсказании роста или падения графика функции, основанной на экспоненциальном росте. Также, график может быть использован для анализа данных и поиска закономерностей. Для этого необходимо применять свойства натурального логарифма на различные значения и наблюдать изменения на графике.

Натуральные логарифмы имеют множество приложений в различных областях: физике, экономике, биологии и др. Используя график натурального логарифма, можно делать более точные прогнозы и проводить более глубокий анализ данных.

Применение натуральных логарифмов в математике

Одно из основных применений натуральных логарифмов — решение экспоненциальных уравнений. Натуральные логарифмы позволяют преобразовывать уравнения в более простую форму, что облегчает их решение. Они помогают найти значения неизвестных переменных в уравнениях, связанных с процентами, ростом и упадком.

Также натуральные логарифмы применяются в различных областях математики, включая анализ функций. Их использование позволяет легко преобразовывать и дифференцировать сложные функции. Они помогают найти производные, определить экстремумы функций и изучить их поведение в различных областях.

В математической статистике натуральные логарифмы играют важную роль при анализе данных. Они помогают преобразовывать данные в более нормальное распределение, что делает их более подходящими для применения статистических методов. Например, при построении регрессионных моделей натуральные логарифмы используются для линеаризации данных и улучшения качества модели.

Кроме того, натуральные логарифмы широко применяются в финансовой математике и экономике. Они используются для моделирования и анализа процентных ставок, сложных процентных формул и дисконтирования денежных потоков. Натуральные логарифмы также пригождаются при изучении вероятности и статистики, особенно при решении задач, связанных с нормальным распределением.

В итоге, натуральные логарифмы играют важную роль в математике и его приложениях. Они позволяют решать уравнения и преобразовывать функции, что помогает упростить и анализировать сложные математические задачи. Их применение в различных областях математики, статистики и экономики позволяет получать более точные и надежные результаты.

Натуральные логарифмы: суть и применение

Суть натуральных логарифмов

Натуральные логарифмы позволяют найти степень, в которую нужно возвести число e, чтобы получить заданное число. То есть, если y = ln(x), то e^y = x. Натуральные логарифмы обратно связаны с экспонентами и позволяют решать уравнения, в которых переменная находится в показателе степени.

Основные свойства натуральных логарифмов:

• ln(1) = 0
• ln(e) = 1
• ln(x * y) = ln(x) + ln(y)
• ln(xⁿ) = n * ln(x)
• ln(1/x) = -ln(x)

Применение натуральных логарифмов

Натуральные логарифмы находят широкое применение в различных областях, таких как:

1. Математика и анализ: используются для решения экспоненциальных уравнений, нахождения пределов, дифференцирования и интегрирования функций.
2. Статистика: применяются для нахождения среднего значения, дисперсии и других статистических показателей.
3. Физика: используются для моделирования и решения определенных физических задач, таких как распределение тепла или радиоактивного распада.
4. Финансы и экономика: применяются для моделирования процентных ставок, капитализации процентов и оценки рисков инвестиций.
5. Биология и медицина: используются для моделирования роста популяции, обработки данных об экспоненциальном росте бактерий или оценки времени распада медикамента в организме.

Натуральные логарифмы являются важным математическим инструментом, который помогает решать сложные задачи в различных областях науки и техники. Их понимание и применение позволяют углубить знания и навыки в математике и других научных дисциплинах.