
Векторы, которые не лежат на одной прямой и не коллинеарны называются неколлинеарными векторами. Эти векторы обладают интересными свойствами, которые можно использовать в различных областях, включая геометрию, физику и информатику. Неколлинеарные векторы помогают в определении направления и перемещения в пространстве, а также в нахождении решений задач линейной алгебры и векторного анализа.
Определение неколлинеарных векторов
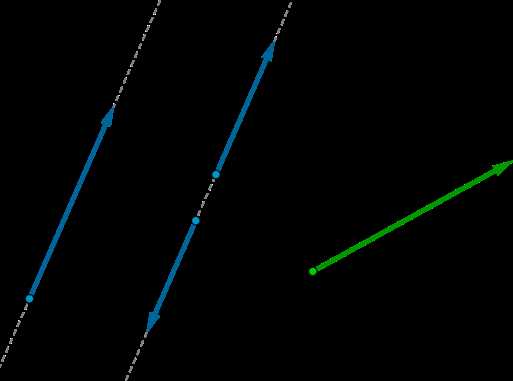
Одним из способов определить неколлинеарность векторов является проверка их линейной независимости. Векторы называются линейно зависимыми, если один из них может быть представлен как линейная комбинация других векторов. Если же векторы линейно независимы, то они неколлинеарны.
Другим способом определения неколлинеарных векторов является их скалярное произведение. Если скалярное произведение ненулевое, то векторы точно неколлинеарны. Если же скалярное произведение равно нулю, то для определения неколлинеарности векторов необходимо провести дополнительные проверки.
Неколлинеарные векторы имеют ряд важных свойств. Например, их линейная комбинация может образовывать любой вектор в плоскости, содержащей эти векторы. Кроме того, неколлинеарные векторы формируют основу линейного пространства и обладают свойством независимости по модулю и направлению.
Неколлинеарные векторы часто используются в различных областях науки и техники, таких как физика, геометрия, компьютерная графика и др. Они помогают решать разнообразные задачи и моделировать реальные явления.
Неколлинеарные векторы: определение и свойства
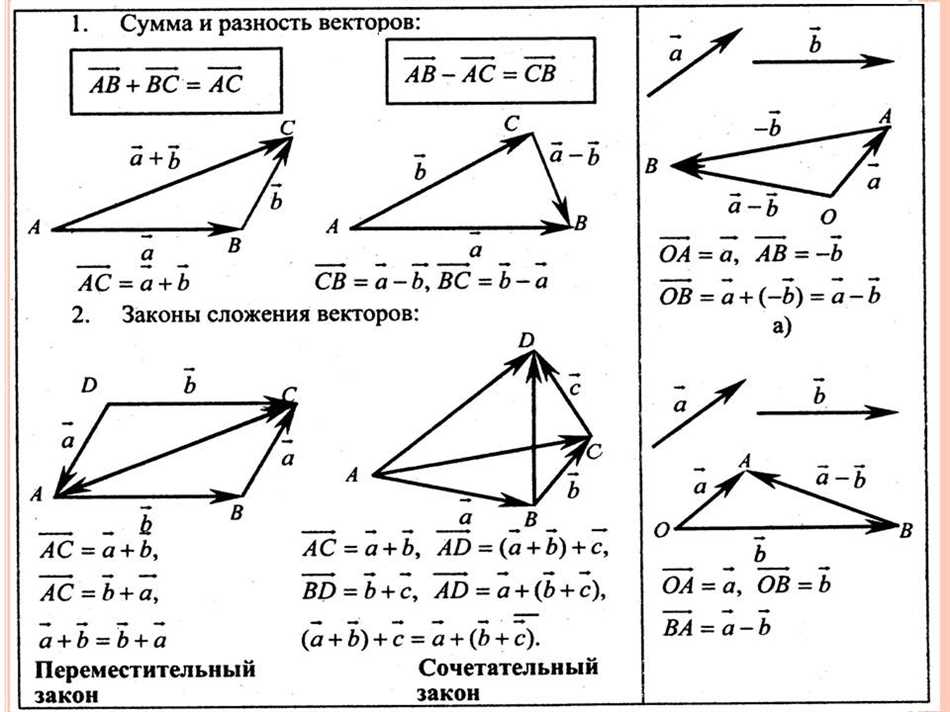
Неколлинеарные векторы обладают следующими свойствами:
- Они обеспечивают достаточную информацию для построения системы координат.
- Они могут быть использованы для определения базиса векторного пространства и построения иных линейных комбинаций.
- Они образуют линейно независимую систему векторов.
- Они могут быть использованы для нахождения площади параллелограмма, построенного на этих векторах. Площадь параллелограмма может быть вычислена с помощью формулы: площадь = |a x b|, где a и b — неколлинеарные векторы.
Неколлинеарные векторы имеют важное значение в геометрии, физике, компьютерной графике и других областях, где требуется работа с векторами.



