Неопределенность в математике: понятие и применение

В математике существует понятие неопределенности, которое означает отсутствие определенного значения или решения. Эта концепция часто вызывает смуту и неуверенность у многих студентов и даже у профессиональных математиков.

Неопределенность проявляется, когда необходимо найти значение или решение, но имеется не достаточно информации или ситуация имеет несколько возможных исходов. Она возникает в различных областях математики, таких как теория вероятностей, дифференциальное исчисление или логика.

Понимание и умение работать с неопределенностью являются важными навыками в математике, а также в жизни. Как философия, неопределенность провоцирует нас к исследованию и поиску разных путей для решения проблем.

Раздел 1: Определение неопределенности

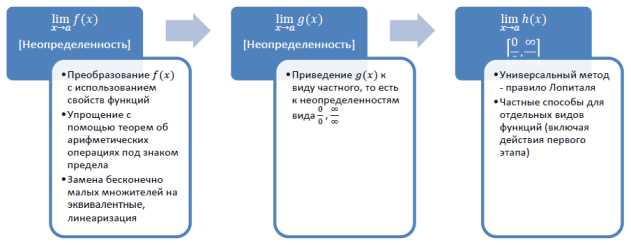
Давайте поговорим о неопределенности. Это понятие, которое стало неотъемлемой частью математики и имеет огромное значение в жизни каждого из нас. Неопределенность возникает тогда, когда у нас есть несколько возможных исходов или результатов, и мы не можем с уверенностью сказать, какой именно из них произойдет.

Сложно представить, как бы выглядел мир без неопределенности. Без него мы бы жили в полной предсказуемости, все было бы заранее известно и не оставалось бы места для сюрпризов и открытий. Неопределенность стимулирует нас и заставляет мыслить, искать решения, пробовать новое и идти вперед.

В математике неопределенность может принимать различные формы. Одной из самых известных форм неопределенности является деление на ноль. Результат такой операции не имеет определенного значения и называется «бесконечность». Это является примером того, как неопределенность может менять наше представление о мире и расширять наши границы понимания.

Неопределенность также проявляется в статистике, когда у нас есть несколько возможных исходов и мы не можем точно предсказать, какой из них произойдет. Например, когда мы бросаем монету, у нас есть две возможности: орел или решка. Но неопределенность заключается в том, что мы не знаем заранее, какой будет результат.

Но не стоит пугаться неопределенности. Она необходима для нашего развития и роста. Она помогает нам принимать решения, преодолевать трудности и находить новые варианты решений. Без неопределенности мы бы ограничили себя и препятствовали своему собственному развитию.

Итак, неопределенность — это нечто, что позволяет нам исследовать новые горизонты, найти новые пути и открыть для себя неизведанные возможности. Поэтому давайте не бойтесь неопределенности, а наоборот, исследуйте и учитеся использовать ее в свою пользу.

Определение неопределенности в математике

Неопределенность в математике — это ситуация, когда невозможно однозначно определить значение или решение задачи. Это происходит, когда мы сталкиваемся с неизвестными, параметрами или условиями, которые могут принимать различные значения или иметь несколько возможных решений.

Концепция неопределенности находит свое применение в различных областях математики, таких как теория вероятностей, алгебра, анализ и др. Эта концепция играет важную роль в статистике и теории решения уравнений.

Рассмотрим пример неопределенности в математике. Представьте, что у нас есть уравнение x + 2 = 6. Мы хотим найти значение x. Очевидно, что x = 4, так как 4 + 2 = 6. Однако, есть и другое возможное решение — x может быть равно -2, так как -2 + 2 = 0. В этом случае у нас есть два возможных значения для x, и мы не можем однозначно определить его.

Неопределенность может возникать и в более сложных математических проблемах. Например, в теории вероятностей мы сталкиваемся с ситуацией, когда мы не можем точно предсказать исход события, так как есть неопределенность или случайный фактор. В анализе неопределенность может возникать из-за неопределенных пределов или разрывов в функциях.

Неопределенность часто встречается и в реальном мире. В жизни нет всегда четких ответов или решений, и математика помогает нам понять и описать эту неопределенность. Знание и понимание неопределенности в математике обогащает наши знания и способствует развитию научного и творческого мышления.

В заключении, неопределенность в математике — это ситуация, когда ответ на вопрос не может быть однозначно определен. Она играет важную роль в различных областях математики и помогает нам понять и объяснить сложные ситуации. Поэтому изучение неопределенности в математике является важным шагом в нашем пути к познанию и пониманию мира.

Роль неопределенности в математических моделях

Когда мы говорим о математических моделях, неопределенность играет важную роль. Она позволяет ученым учесть различные факторы, которые могут влиять на итоговый результат. Но что такое неопределенность и как она может быть использована в математических моделях?

Неопределенность – это неизвестность или нечеткость входных данных или параметров модели. В реальном мире мы часто сталкиваемся с неопределенностью, потому что мы не можем знать все детали или предсказать будущие события с абсолютной точностью. Например, если мы хотим спрогнозировать погоду, мы можем знать о текущей температуре и атмосферных условиях, но мы не можем учесть все факторы, которые могут повлиять на погоду в будущем.

Тем не менее, неопределенность не должна рассматриваться только как проблема. На самом деле, она может быть полезным инструментом в математических моделях. Рассмотрим следующий пример. Представим себе, что мы строим модель для прогнозирования продаж в нашей компании. У нас есть данные о продажах за последние несколько лет, но нам также нужно учесть возможные факторы, которые могут влиять на продажи в будущем, такие как экономическая ситуация или маркетинговые кампании конкурентов.

Здесь неопределенность приходит на помощь. Мы можем создать математическую модель, которая учитывает различные сценарии и возможности. Мы можем использовать статистические методы, чтобы определить вероятность каждого сценария и их влияние на продажи. Таким образом, мы можем сделать более точные прогнозы и принять решения на основе этой информации.

Неопределенность также помогает нам оценить риски. Если мы знаем, что некоторые параметры имеют большую степень неопределенности, мы можем включить эту информацию в нашу модель и определить вероятность возникновения неблагоприятных событий. Это позволяет нам принимать предусмотрительные меры и разработать стратегии для управления рисками.

Кроме того, неопределенность может также позволить нам исследовать неизвестные области и делать новые открытия. Нередко неопределенность побуждает ученых к дальнейшему исследованию и экспериментам, чтобы лучше понять и моделировать сложные феномены.

Таким образом, неопределенность – это необходимый элемент математических моделей. Она позволяет учесть различные факторы, оценить риски и разрабатывать стратегии для управления неопределенностью. Благодаря неопределенности мы можем делать более точные прогнозы и принимать осознанные решения в условиях неопределенности.

Раздел 2: Примеры неопределенности

Перейдем к разбору примеров неопределенности в математике, чтобы лучше понять, как эти ситуации могут возникать и как их можно решить.

1. Ноль делить на ноль

Одним из наиболее известных примеров неопределенности является деление нуля на ноль. Когда мы делим любое число на ноль, результат неопределен, так как не существует числа, которое можно умножить на ноль и получить исходное число.

Что это означает для нас? Это означает, что мы не можем точно определить значение, когда ноль делится на ноль. Например, если у нас есть выражение 0/0, то мы не можем сказать, равно ли оно нулю, единице или любому другому числу. В таких случаях мы говорим, что результат деления нуля на ноль неопределен.

2. Бесконечность минус бесконечность

Другим примером неопределенности является вычитание бесконечности из бесконечности. Например, если у нас есть выражение ∞ — ∞, то не существует однозначного ответа на вопрос, какое число получится в итоге.

Почему это происходит? Представьте, что у вас есть бесконечное количество красных и синих шариков, и вы вычитаете одно бесконечное количество из другого. Сколько шариков у вас останется? Очевидно, что здесь нет точного ответа.

Таким образом, вычитание бесконечности из бесконечности является примером неопределенности, когда мы не можем точно определить значение.

3. Определение нуля в степени ноль

Еще одним примером неопределенности является определение нуля в степени ноль. В математике мы знаем, что любое число, возведенное в степень ноль, равно единице. Однако, когда речь идет о нуле в степени ноль, ситуация меняется.

Мы не можем однозначно определить, чему равно ноль в степени ноль. На первый взгляд кажется, что это должно быть равно нулю, так как мы умножаем ноль само на себя несколько раз. Однако, существуют другие рассуждения и точки зрения, которые говорят, что ноль в степени ноль должно быть равно единице.

Таким образом, определение нуля в степени ноль является примером неопределенности, где математики до сих пор продолжают исследовать и обсуждать этот вопрос.

Итак, в математике существует много примеров неопределенности, которые могут вызывать различные точки зрения и дебаты. Однако, эта неопределенность также открывает двери для новых открытий и исследований в математике. Что думаете вы о такой неопределенности? Вам интересно узнать больше о сложных проблемах в математике?

Пример 1: Неопределенность в вычислениях

Представьте себе, что вы пытаетесь решить простое уравнение: 2x + 5 = 15. Вы поделили обе стороны на 2 и получили x + 5/2 = 7. Затем, вы отняли 5/2 от обеих сторон и получили x = 7 — 5/2. После выполнения арифметических операций, мы получили ответ x = 17/2.

Так, мы успешно решили уравнение, исключили неизвестную переменную и получили конкретный ответ. Но что, если я скажу вам, что x может быть и другим числом? Позвольте мне объяснить.

Вычисления все еще корректны, и мы можем продолжать представлять исходное уравнение как 2x + 5 = 15. Если мы теперь поделим обе стороны на 2, мы получим x + 5/2 = 7. Затем мы отнимем 5/2 от обеих сторон и получим x = 7 — 5/2.

На этом этапе мы сталкиваемся с интересной ситуацией: мы имеем неоднозначность в выражении для x. Если мы продолжим вычисления, мы получим x = 17/2, как и ранее. Но мы также можем представить 7 — 5/2 как другой дробный ответ, например, x = 6/2. Оба ответа являются математически корректными решениями этого уравнения.

Таким образом, в данном примере мы сталкиваемся с неопределенностью в выражении для x. Вместо того чтобы выделять одно конкретное значение ответа, мы можем представить несколько вариантов ответов, которые будут верными.

Такие ситуации часто возникают в математике, особенно в вычислениях, где они могут представлять вызов для нас, чтобы выяснить все возможные значения. Это исследование и поиск различных вариантов ответов делает математику увлекательной и стимулирующей.

Так что, вместо того, чтобы относиться к неопределенности в вычислениях как к проблеме, посмотрите на это как на возможность для исследования и расширения своего понимания математики. Кто знает, какую интересную находку вы можете сделать, когда сталкиваетесь с этим вызовом? Удивительно, как некоторые неопределенности могут привести к новым идеям и открытиям в мире математики!

Неопределенность в математике: понятие и применение

Неопределенность может возникать в различных областях математики, таких как алгебра, арифметика, геометрия и т. д. Она может быть вызвана недостаточной информацией, неполными или противоречивыми условиями задачи, невозможностью заранее предсказать поведение математического объекта или ограничениями самой математической теории.

Примеры неопределенности в математике:

1. Деление на ноль: Результат деления любого числа на ноль неопределен, так как невозможно поделить что-либо на ноль.
2. Неопределенная форма: В некоторых математических операциях, таких как вычисление предела или решение уравнений, могут возникать неопределенные формы, когда результат не может быть однозначно определен.
3. Неизвестные переменные: Если у нас есть математическое выражение или уравнение с неизвестными переменными, то результат может быть неопределен, пока не будут известны значения этих переменных.

Неопределенность является важным понятием в математике, так как она позволяет учитывать различные возможности и ограничения в решении задач. Она помогает исследовать различные случаи и анализировать поведение математических объектов в различных ситуациях. Неопределенность также может быть полезным инструментом для выявления проблем в постановке задачи или проверки правильности решения.