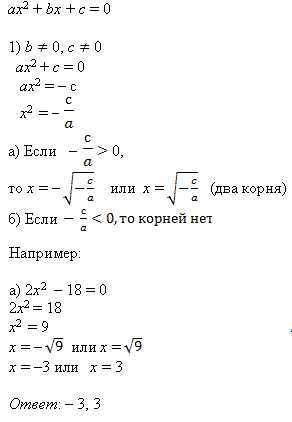
Когда мы говорим о квадратных уравнениях, часто всплывает понятие «неполного квадратного уравнения». Что это такое и как оно отличается от обычного квадратного уравнения? Неполное квадратное уравнение — это квадратное уравнение, в котором отсутствует один из коэффициентов. Обычно, при решении квадратных уравнений, мы сталкиваемся с выражениями вида ax^2 + bx + c = 0, где a, b и c — это числа. Однако, в неполном квадратном уравнении может отсутствовать один из этих коэффициентов. Давайте рассмотрим несколько примеров, чтобы лучше понять это понятие.
- Неполное квадратное уравнение: определение и примеры
- Пример 1:
- Пример 2:
- Виды неполных квадратных уравнений
- Примеры неполных квадратных уравнений
- Пример 1
- Пример 2
- Пример 3
- Как решать неполные квадратные уравнения
- Методы решения неполных квадратных уравнений
- Неполное квадратное уравнение: определение и примеры
Неполное квадратное уравнение: определение и примеры
Неполное квадратное уравнение представляет собой квадратное уравнение, которое содержит только одну переменную во второй степени, без линейного или свободного члена. А что вообще такое квадратное уравнение? Отличный вопрос! Квадратное уравнение — это уравнение вида ax^2 + bx + c = 0, где a, b и c — это коэффициенты уравнения, причем а ≠ 0.
Итак, теперь, когда мы разобрались с определением неполного квадратного уравнения, давайте рассмотрим несколько примеров.
Пример 1:

Рассмотрим уравнение x^2 = 16. Это неполное квадратное уравнение, так как у него нет линейного или свободного члена. Чтобы найти значения переменной x, нам необходимо извлечь квадратный корень из обеих сторон уравнения.
√(x^2) = √16
x = ±4
Таким образом, решением данного неполного квадратного уравнения являются значения x = 4 и x = -4.
Пример 2:
Рассмотрим уравнение 9x^2 = 36. В данном случае есть коэффициент перед переменной, но нет свободного члена. Чтобы решить его, сначала нужно разделить обе части уравнения на 9.
x^2 = 4
√(x^2) = √4
x = ±2
Таким образом, решением данного неполного квадратного уравнения являются значения x = 2 и x = -2.
Теперь, когда мы рассмотрели несколько примеров неполных квадратных уравнений, вы, наверняка, стали понимать их суть лучше. Они могут показаться простыми, но все же необходимо аккуратно работать с алгебраическими операциями и не забывать проверять полученные значения.
Так что давайте потренируемся решать неполные квадратные уравнения на своей истинной суть и достигать успеха! Удачи вам!
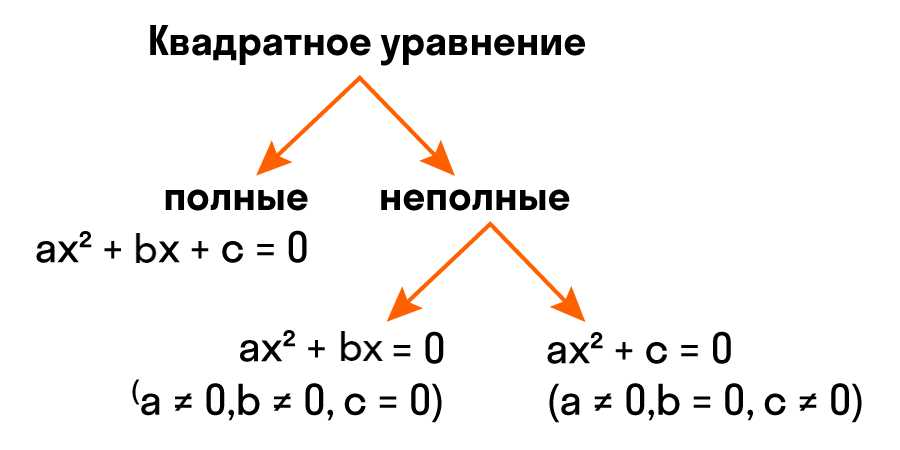
Виды неполных квадратных уравнений
Давайте поговорим о неполных квадратных уравнениях. Это уравнения вида ax^2 + bx + c = 0, где коэффициент a не равен нулю. Они имеют много интересных свойств и могут быть полезными для различных задач.
Первый вид неполных квадратных уравнений, о котором хотелось бы поговорить, — это квадратные уравнения без линейного члена, то есть уравнения вида ax^2 + c = 0. В таких уравнениях коэффициент b равен нулю. Они могут возникать в различных задачах, например, при моделировании физических процессов.
Второй вид неполных квадратных уравнений — это квадратные уравнения без константного члена, то есть уравнения вида ax^2 + bx = 0. В таких уравнениях коэффициент c равен нулю. Этот вид уравнений встречается, например, при решении задач, связанных с геометрией или оптимизацией.
И последний вид неполных квадратных уравнений, о котором хотелось бы упомянуть, — это квадратные уравнения с отсутствующими как линейным, так и константным членами, то есть уравнения вида ax^2 = 0. В таких уравнениях и b, и c равны нулю. Они могут возникать, например, при анализе равновесия в физических системах или при решении задач на поиск экстремумов.
Таким образом, неполные квадратные уравнения представляют собой разные варианты обычного квадратного уравнения. Они широко применяются в различных областях науки и техники, и познание их особенностей может быть полезным.
Примеры неполных квадратных уравнений
Пример 1
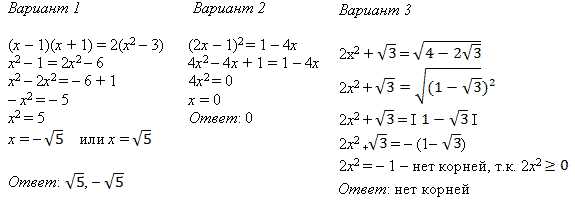
Рассмотрим уравнение:
x^2 — 9 = 0
В этом уравнении отсутствует линейный член, и у нас есть только квадратный член, представленный в виде x^2. Чтобы решить это уравнение, мы должны найти значения x, которые удовлетворяют условию x^2 — 9 = 0.
Для начала мы можем перенести -9 на другую сторону уравнения:
x^2 = 9
Затем мы можем извлечь квадратный корень из обеих сторон уравнения, чтобы получить значение x:
x = ±√9
x = ±3
Таким образом, уравнение x^2 — 9 = 0 имеет два решения: x = 3 и x = -3.
Пример 2
Рассмотрим другое уравнение:
x^2 + 16 = 0
В этом уравнении отсутствует линейный член, и у нас есть только квадратный член, представленный в виде x^2. Однако здесь есть дополнительное слагаемое 16. Чтобы решить это уравнение, мы должны найти значения x, удовлетворяющие условию x^2 + 16 = 0.
Мы можем перенести 16 на другую сторону уравнения, меняя его знак:
x^2 = -16
Теперь нам необходимо извлечь квадратный корень из отрицательного числа, что невозможно в множестве действительных чисел. Это означает, что уравнение x^2 + 16 = 0 не имеет действительных корней. Однако, в множестве комплексных чисел, у нас есть два мнимых корня: x = 4i и x = -4i, где i — мнимая единица.
Таким образом, данное уравнение в множестве действительных чисел не имеет решений, но в множестве комплексных чисел имеет два мнимых корня: x = 4i и x = -4i.
Пример 3
Рассмотрим еще одно уравнение:
4x^2 = 64
В этом уравнении отсутствуют как линейный, так и свободный члены. Уравнение содержит только квадратный член и постоянное число (64). Чтобы решить это уравнение, мы должны найти значения x, удовлетворяющие условию 4x^2 = 64.
Сначала мы можем разделить обе стороны уравнения на 4:
x^2 = 16
Затем мы можем извлечь квадратный корень из обеих сторон уравнения:
x = ±√16
x = ±4
Таким образом, уравнение 4x^2 = 64 имеет два решения: x = 4 и x = -4.
Надеюсь, эти примеры помогли вам лучше понять, что такое неполное квадратное уравнение и как их решать. Если у вас есть какие-либо вопросы, не стесняйтесь задавать их в комментариях! Желаю вам успехов в изучении математики!
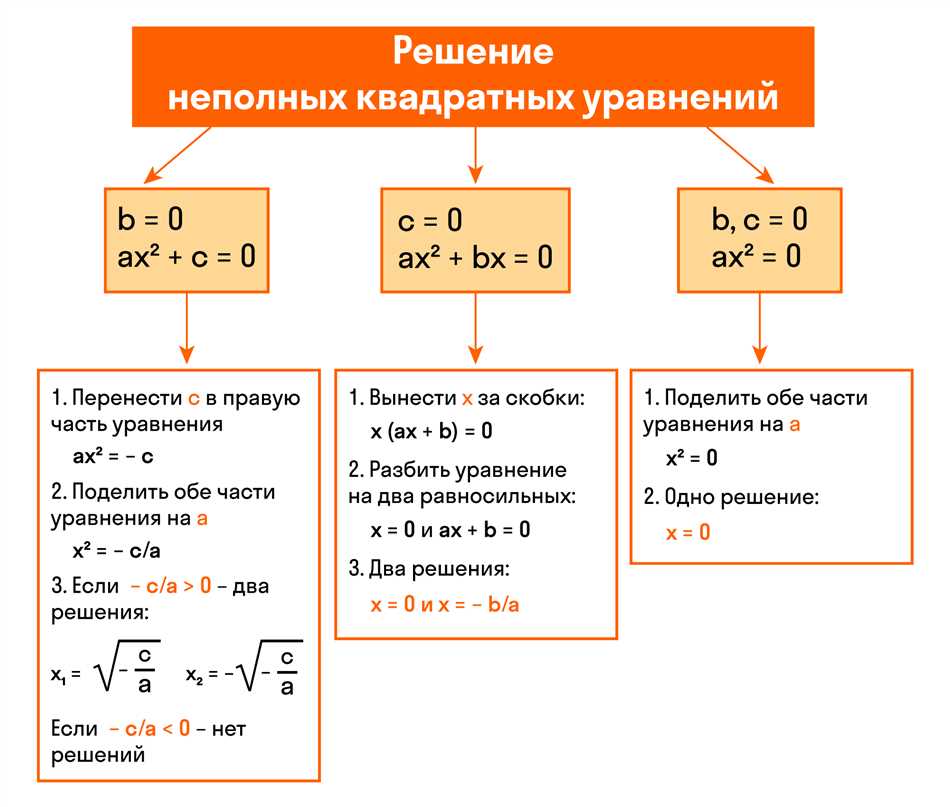
Как решать неполные квадратные уравнения
Перед тем, как мы приступим к решению неполных квадратных уравнений, давайте вспомним, что такое квадратное уравнение. Квадратное уравнение имеет вид ax^2 + bx + c = 0, где a, b и c — это коэффициенты, а x — переменная, которую мы и будем искать.
Теперь перейдем к неполным квадратным уравнениям. Неполное квадратное уравнение имеет вид ax^2 + bx = 0 или ax^2 + c = 0. Здесь отсутствует один из коэффициентов — либо b, либо c. Как же нам решать такие уравнения?
Давайте начнем с случая, когда отсутствует коэффициент b. Итак, у нас есть уравнение ax^2 = 0. Заметим, что если умножить любое число на 0, то результат всегда будет равен 0. Это значит, что для решения данного уравнения, достаточно найти такие значения x, при которых ax^2 = 0. Такое возможно только в двух случаях: когда a = 0 или x = 0. Таким образом, мы получаем два возможных решения: x = 0 или a = 0.
Теперь давайте рассмотрим случай, когда отсутствует коэффициент c. Имеем уравнение ax^2 + bx = 0. В данном случае, у нас есть два слагаемых, которые равны 0. Это значит, что одно из них должно быть равно 0. Раскрываем скобки и получаем два возможных решения: x = 0 или ax + b = 0. Отсюда можно найти значение x, равное -b/a.
Таким образом, мы рассмотрели два случая неполных квадратных уравнений и смогли найти их решения. Надеюсь, что теперь вам стало яснее, как работать с такими уравнениями. Не забывайте проверять свои ответы, подставляя полученные значения x в исходное уравнение и убедитесь, что равенство выполняется.
Удачи вам в решении квадратных уравнений! Если у вас есть какие-либо вопросы, не стесняйтесь задавать — я всегда готов помочь!
Методы решения неполных квадратных уравнений
1. Метод дополнения до полного квадратного уравнения
Один из самых распространенных методов решения неполного квадратного уравнения — метод дополнения до полного квадратного уравнения. Для этого следует добавить к обеим сторонам уравнения квадрат некоторого числа. Например, если у нас есть уравнение 3x^2 + 5x = 8, мы можем добавить 9 к обеим сторонам, чтобы получить полное квадратное уравнение (3x^2 + 5x + 9 = 17).
2. Метод факторизации
Другой метод решения неполного квадратного уравнения — это метод факторизации. Сначала необходимо перенести все члены с x на одну сторону уравнения, чтобы получить уравнение вида ax^2 + bx = 0. Затем можно вынести общий множитель x из каждого члена, что приводит к уравнению x(ax + b) = 0. Нули этого уравнения могут быть найдены путем приравнивания каждого фактора к нулю (x = 0 и ax + b = 0).
3. Использование квадратного корня
Еще один метод решения неполного квадратного уравнения — это использование квадратного корня. Для этого сначала нужно перенести все члены квадратного уравнения на одну сторону, чтобы получить уравнение вида ax^2 + bx = c. Затем можно воспользоваться свойствами квадратного корня, чтобы извлечь корень от обеих сторон уравнения и получить два возможных значения для x.
Итак, вот три метода решения неполных квадратных уравнений – метод дополнения до полного квадратного уравнения, метод факторизации и использование квадратного корня. Каждый из этих методов имеет свои преимущества и может быть применен в зависимости от конкретной ситуации. Попробуйте их и выберите тот, который наиболее подходит к вашему уравнению. Удачи в решении задач!
Неполное квадратное уравнение: определение и примеры
eq0$.
В таком уравнении отсутствует один из коэффициентов, либо равен нулю. Наиболее распространены два случая:
- Когда $a=0$:
- Когда $c=0$:
Если коэффициент $a$ равен нулю, то уравнение превращается в обычное линейное: $bx+c=0$. Данное уравнение решается элементарно, и его решение можно найти с помощью формулы $x=-\frac{c}{b}$.
Если коэффициент $c$ равен нулю, то уравнение принимает вид $ax^2+bx=0$. В этом случае приводим уравнение к виду $x(ax+b)=0$. Отсюда следует, что либо $x=0$, либо $ax+b=0$. Первый вариант даёт нам одно решение $x=0$, второй вариант является линейным уравнением и его решение находится по аналогии с предыдущим пунктом.
| Уравнение | Случай | Решение |
|---|---|---|
| $x^2+3x=0$ | $c=0$ | $x=0$ или $x=-3$ |
| $2x^2-5x=0$ | $c=0$ | $x=0$ или $x=\frac{5}{2}$ |
| $4x^2-16=0$ | $b=0$ | $x=2$ или $x=-2$ |
| $3x^2-2x=0$ | $c=0$ | $x=0$ или $x=\frac{2}{3}$ |