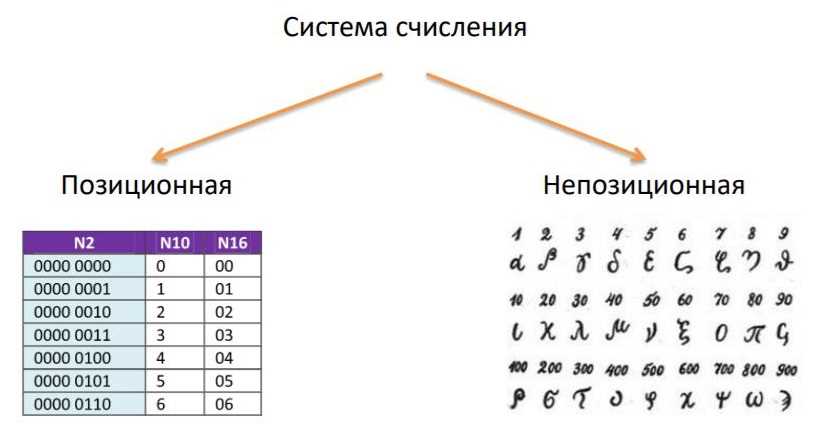
В мире существует несколько различных систем счисления, и одной из них является непозиционная система счисления. В отличие от позиционных систем, где значение цифры зависит от ее позиции в числе, в непозиционных системах каждая цифра имеет свое значение, независимо от ее места в числе.
Непозиционная система счисления нашла применение в различных областях, включая компьютерную науку, математику и информационную безопасность. Примером использования такой системы может быть шифрование данных, где каждая цифра или символ заменяется на другую цифру или символ, чтобы зашифровать информацию и защитить ее от несанкционированного доступа. В технических системах также используется непозиционная система счисления для представления различных видов данных, таких как цвета и звуки, которые не могут быть точно выражены в позиционных системах.
Описание

За пределами математики и компьютерных наук непозиционная система счисления может показаться необычной или непривычной. Однако она находит свое применение в различных областях, включая логистику, информационную безопасность, криптографию и кодирование данных.
Непозиционная система счисления может использоваться для создания специальных кодов, которые обеспечивают дополнительную безопасность и защиту информации. Например, в шифровании может применяться система счисления, где каждая цифра представляет собой определенный символ или символьную комбинацию.
Эта система счисления также может быть полезна в логистике, где требуется точное и непротиворечивое обозначение изделий или товаров. Например, каждый товар может быть пронумерован уникальным кодом, состоящим из цифр, где каждая цифра представляет определенные характеристики товара, такие как вес, размер или цвет.
Кроме того, непозиционная система счисления может использоваться для создания специализированных алгоритмов, которые могут эффективно решать определенные задачи. Например, непозиционные системы счисления могут быть использованы для оптимизации вычислений или решения сложных математических проблем.
Хотя непозиционная система счисления не является основным методом представления чисел в повседневной жизни, она все же играет важную роль в некоторых областях и предоставляет уникальные возможности для решения различных задач.
Преимущества непозиционной системы счисления
1. Простота и понятность
Непозиционная система счисления обладает простотой и понятностью в использовании. В ней каждая цифра имеет определенное значение, и их комбинация позволяет образовывать числовые значения. Это делает систему легко воспринимаемой и доступной для людей всех возрастов и уровней математической грамотности.
2. Гибкость и расширяемость
Непозиционная система счисления позволяет гибко менять количество и значения символов в системе. В позиционной системе счисления изменение основания системы требует также изменения всех существующих чисел. Но в непозиционной системе можно добавлять или удалять символы без влияния на уже существующие числа.
3. Простота операций
В непозиционной системе счисления процесс выполнения математических операций, таких как сложение, вычитание, умножение и деление, также упрощается. Нет необходимости учитывать позиции цифр и производить переносы при сложении и вычитании. Это значительно ускоряет процесс выполнения операций и упрощает их для понимания.
- 4. Эффективность при работе с большими числами
Непозиционная система счисления также показывает свои преимущества при работе с большими числами. В позиционной системе при добавлении новых разрядов (чисел) нужно увеличивать их количество, тогда как в непозиционной системе достаточно просто добавить новый символ. Это делает работу с большими числами более эффективной и удобной в непозиционной системе счисления.
Итак, непозиционная система счисления предлагает ряд значимых преимуществ перед позиционной системой. Она обладает простотой и понятностью, гибкостью и расширяемостью, а также упрощает выполнение операций и работу с большими числами. Все это делает ее привлекательной и эффективной системой счисления, которую можно использовать в различных ситуациях и областях жизни.
Примеры использования непозиционной системы счисления
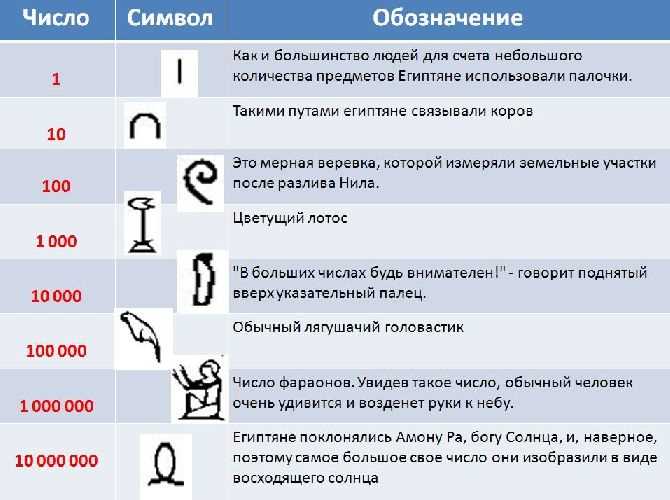
Одним из примеров использования непозиционной системы счисления является римская система. В римской системе используются следующие символы для обозначения чисел: I (1), V (5), X (10), L (50), C (100), D (500), M (1000). Как видно, значение каждого символа не зависит от его позиции в числе. Например, число IX состоит из символов I и X, которые представляют значения 1 и 10 соответственно. Сумма этих значений равна 9.
Римская система широко использовалась в Древнем Риме для записи чисел и в настоящее время ее символы часто встречаются в архитектуре и искусстве. Она также используется в некоторых областях, которые имеют свои традиции или символику, например, при записи номеров частей, каталогов, годов основания организаций и т.д.
Еще одним примером непозиционной системы счисления является бинарная система. В бинарной системе используются всего два символа — 0 и 1. Здесь также значение каждого символа не зависит от его позиции. Например, число 1011 в бинарной системе представляет собой сумму значений символов: 1*2^3 + 0*2^2 + 1*2^1 + 1*2^0, что равно 11 в десятичной системе счисления.
Бинарная система широко используется в компьютерной технике, где каждый символ 0 или 1 представляет логическое состояние (включено/выключено) или двоичное значение. Все данные в компьютере, включая числа, текст и изображения, хранятся и передаются в виде двоичных чисел в памяти компьютера и на жестком диске.
Непозиционные системы счисления имеют свои преимущества и недостатки по сравнению с позиционными системами. Они могут быть эффективными для представления определенных типов данных или для решения конкретных задач. Однако в повседневной жизни мы обычно используем десятичную систему счисления, которая является позиционной и более привычной для нас.
Сравнение непозиционной и позиционной системы счисления
Непозиционная система счисления и позиционная система счисления представляют разные подходы к записи чисел. В позиционной системе счисления значение цифры зависит от ее позиции в числе, а в непозиционной системе счисления значение каждой цифры не зависит от ее позиции. В этом отношении они отличаются друг от друга.
Позиционная система счисления является более распространенной и широко используется в нашей повседневной жизни. Она основана на использовании базовых цифр и их позиций для представления чисел. Например, в десятичной системе счисления мы используем 10 базовых цифр от 0 до 9 и позиции этих цифр определяют их значения в числе. Это позволяет нам записывать и работать с большими числами и выполнять сложные математические операции.
С другой стороны, непозиционная система счисления, такая как римская система, не использует позиции цифр для определения их значений. Вместо этого она использует различные символы для представления чисел. Например, в римской системе счисления символ «I» представляет число 1, символ «V» представляет число 5 и так далее. Для записи чисел в непозиционной системе счисления необходимо знать и помнить значения каждого символа. Это может быть более сложным и запутанным процессом, особенно при работе с большими числами.
Хотя непозиционная система счисления имеет свои особенности и может использоваться в определенных контекстах, позиционная система счисления является более удобной и практичной для повседневных вычислений и приложений. Она позволяет нам легко работать с числами разных величин и выполнить различные операции, такие как сложение, вычитание, умножение и деление. С ее помощью мы можем легко передавать информацию и осуществлять точные вычисления.
В итоге, позиционная система счисления представляет собой более универсальный и эффективный способ работы с числами, который широко применяется в нашей жизни. Хотя непозиционная система счисления может иметь свои преимущества в определенных областях, она ограничена в своих возможностях и не так удобна для повседневных вычислений и приложений.
Применение в компьютерных науках
Непозиционная система счисления имеет широкое применение в компьютерных науках. В компьютерах и электронных устройствах информация обычно представлена в виде двоичного кода, где только два возможных значения: 0 и 1. Но чтобы упростить работу с числами в компьютерах, использование непозиционной системы счисления может быть крайне полезным.
Одним из примеров использования непозиционной системы счисления в компьютерных науках является шифрование данных. Криптографические алгоритмы часто требуют выполнения сложных математических операций, таких как возведение в степень или умножение больших чисел. Непозиционная система счисления может помочь упростить эти операции и повысить эффективность шифрования.
Кроме того, непозиционная система счисления используется в процессе кодирования и сжатия данных. Для представления цветов в изображениях часто используется формат RGB, в котором каждый цвет представлен числами от 0 до 255. Вместо использования десятичной системы счисления, непозиционная система счисления может быть использована для более компактного представления этих чисел.
Также, для оптимизации вычислительных операций в компьютерных программах, непозиционна система счисления может быть использована для представления чисел с плавающей точкой. Это позволяет ускорить выполнение математических операций и повысить производительность программ.
Как видите, непозиционная система счисления нашла широкое применение в компьютерных науках. Она помогает упростить и оптимизировать различные вычислительные операции, а также улучшить криптографическую защиту данных и сжатие информации. Без нее современные компьютерные технологии были бы невозможны.
Непозиционная система счисления и примеры ее использования
Примеры непозиционных систем счисления:
- Двоичная система счисления — основывается на использовании только двух цифр: 0 и 1. Каждая цифра в двоичной системе счисления имеет свое собственное значение, которое не меняется в зависимости от положения цифры в числе. Например, число 101 в двоичной системе счисления обозначает 1*2^2 + 0*2^1 + 1*2^0 = 5.
- Тринарная система счисления — основывается на использовании трех цифр: 0, 1 и 2. Каждая цифра в тринарной системе счисления имеет свое собственное значение, которое не меняется в зависимости от положения цифры в числе. Например, число 102 в тринарной системе счисления обозначает 1*3^2 + 0*3^1 + 2*3^0 = 11.
- Шестнадцатеричная система счисления — основывается на использовании шестнадцати цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. Каждая цифра в шестнадцатеричной системе счисления имеет свое собственное значение, которое не меняется в зависимости от положения цифры в числе. Например, число 1A в шестнадцатеричной системе счисления обозначает 1*16^1 + 10*16^0 = 26.
Непозиционная система счисления находит применение в различных областях, таких как компьютерные науки, электроника, криптография и др. Например, двоичная система счисления используется для представления и обработки информации в компьютерах, а шестнадцатеричная система счисления используется в программировании для более удобного представления и работы с двоичными числами.






