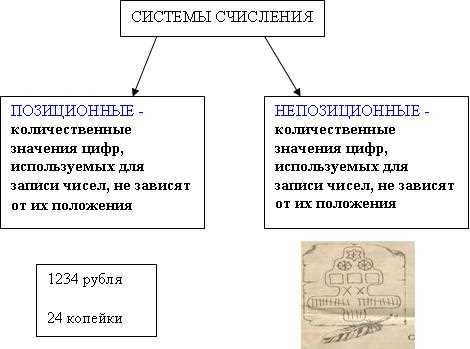
Когда мы говорим о системах счисления, обычно в мыслях возникают десятичная или двоичная системы, которые широко применяются в информатике. Но есть и другие системы счисления, которые не следуют строгим правилам позиционной системы. Одной из таких систем является непозиционная система счисления.
Непозиционная система счисления основана на использовании отдельных символов или групп символов для представления чисел. В отличие от позиционной системы, где каждый разряд имеет свою степень, в непозиционной системе каждый символ несет определенную ценность.
Особенностью непозиционной системы счисления является то, что она может быть более экономичной и эффективной в применении для определенных задач. Она также может быть сложнее для понимания и использования, поскольку требует знания соответствующих символов и их значений.
Основные понятия
В информатике существуют различные системы счисления, в том числе популярные десятичная и двоичная системы. Однако, помимо них, существуют и другие, менее распространенные. Одной из таких систем является непозиционная система счисления.
Непозиционная система счисления отличается от позиционной тем, что каждая цифра числа имеет свою независимую значение. В позиционной системе счисления, например, в десятичной, значение цифры зависит от ее позиции в числе. Так, цифра 2 в числе 123 имеет значение 20, цифра 3 — 30, а цифра 1 — 100.
В непозиционной системе счисления каждая цифра числа имеет свою фиксированную величину. Так, в системе счисления с основанием 4 каждой цифре присваивается следующая величина: 1, 4, 16, 64 и т.д. К примеру, число 1242 в такой системе будет иметь следующее значение: 1*64 + 2*16 + 4*4 + 2*1 = 64 + 32 + 16 + 2 = 114.
Важно помнить, что непозиционная система счисления имеет свои особенности и специфику. Она может использоваться в информатике для определенных задач, где требуется нестандартный подход и гибкость. Например, в системе счисления с основанием 60 используется в музыке для обозначения музыкальных интервалов и нот, а также в измерениях времени и углов.
Теперь, когда мы знаем основные понятия непозиционной системы счисления, нам будет легче понять ее принципы и применение в информатике. Это интересная и увлекательная тема, которая расширит наши знания и позволит решать различные задачи с использованием нестандартных методов. Представьте, какой мощью оснастит нас такой арсенал инструментов!
Принцип работы непозиционной системы счисления

В непозиционной системе счисления, значение числа определяется набором символов и их порядком. Каждому символу присваивается определенное значение, и они комбинируются вместе, чтобы представлять числа. Например, в непозиционной системе счисления символы «A», «B» и «C» могут иметь значения 1, 2 и 3 соответственно.
Принцип работы непозиционной системы счисления может быть легче понять на примере. Представим, что у нас есть число 321, и мы хотим записать его в непозиционной системе счисления, где символы A, B и C обозначают значения 1, 2 и 3. Мы могли бы представить число 321 с использованием символов BBAACB, где два символа B представляют значение 2, символ A представляет значение 1, и символ C представляет значение 3.
Основное преимущество непозиционной системы счисления — это то, что она может быть проще для определенных вычислений или алгоритмов. Непозиционная система счисления может использоваться, например, для отправки и приема данных в компьютерных сетях, где символы могут представлять определенные биты или байты информации.
Теперь, давайте представим, что у нас есть задача по сложению двух чисел в непозиционной системе счисления. Мы можем сложить символы, как обычные числа, присваивая значения символам и вычисляя их сумму. Например, если у нас есть числа BBAACB и BCBABA, мы сначала преобразуем их в значения 321 и 213 соответственно, затем сложим их и получим 534 в нормальной десятичной системе счисления.
Таким образом, принцип работы непозиционной системы счисления заключается в использовании символов, которым присваиваются определенные значения, и комбинировании их для представления чисел. Эта система может быть полезной в различных областях информатики и вычислений, где позиционная система счисления может быть неэффективна или неудобна.
Преимущества и недостатки непозиционной системы счисления в информатике
Одним из очевидных преимуществ непозиционной системы счисления в информатике является возможность более компактного хранения и передачи числовой информации. В позиционной системе счисления каждая цифра требует определенного количества битов для представления, в то время как в непозиционной системе количество битов для представления числа зависит от значения каждой цифры. Это позволяет снизить объем используемой памяти и уменьшить время передачи данных.
Кроме того, непозиционная система счисления обладает большей гибкостью при работе с числами разной сложности. В позиционной системе счисления сложение, вычитание, умножение и деление требуют выполнения арифметических операций в зависимости от позиции цифр. В непозиционной системе счисления можно выполнять операции с любыми цифрами, не задумываясь о позиции. Это упрощает и ускоряет выполнение математических операций.
Однако, непозиционная система счисления имеет и свои недостатки. Одним из них является сложность чтения и понимания числовых значений. В позиционной системе счисления, где позиция цифры определяет вес и значение этой цифры, легко определить, какое число больше или меньше. В непозиционной системе счисления это требует дополнительных вычислений и становится более сложным и трудоемким процессом.
Еще одним недостатком непозиционной системы счисления является отсутствие единого стандарта. В отличие от позиционной системы, где существует универсальный стандарт, такой как десятичная или двоичная система, непозиционная система счисления не имеет конкретной нумерации или документированного формата представления чисел. Это создает сложности при обмене информацией и взаимодействии между различными системами и программами.
В целом, непозиционная система счисления имеет свои преимущества и недостатки. Она может быть полезна в определенных ситуациях, таких как эффективное хранение и передача числовых значений, но также требует дополнительных вычислений и может вызывать сложности при работе с числами разной сложности. Поэтому необходимо внимательно оценивать преимущества и недостатки непозиционной системы счисления при ее использовании в информатике.
Непозиционная система счисления в информатике: определение и особенности
Особенности непозиционной системы счисления:
- Могут использоваться различные символы для обозначения разных значений, что позволяет использовать алфавиты разных языков или специальные символы для обозначения чисел или операций.
- Отсутствует дискретизация чисел, что означает возможность использования чисел с плавающей точкой и повышает точность вычислений.
- Большая гибкость при проведении различных операций, таких как сложение, вычитание, умножение и деление.
- Однако, непозиционная система счисления обладает некоторыми ограничениями в сравнении с позиционной системой, такими как усложнение операций сложения и умножения чисел из-за необходимости выполнения более продолжительных вычислений.
Непозиционные системы счисления могут использоваться в различных областях информатики, например, для представления чисел с плавающей точкой или для работы с специфическими алгоритмами, требующими нестандартных операций со значениями чисел.