Неравенство в математике — это важная тема, которая помогает нам сравнивать значения чисел и выражений. В математике мы часто сталкиваемся с различными видами неравенств, которые помогают нам определить отношение между числами. Знание правил и определения неравенств позволяет нам решать задачи и проводить различные анализы. В этой статье мы рассмотрим основные понятия и правила неравенств в математике, которые помогут вам лучше понять и применять это понятие в своих задачах и уравнениях.
Основные понятия
Когда мы говорим о неравенствах в математике, мы обращаемся к правилам и определениям, которые помогают нам сравнивать числа и выражения. Основные понятия неравенств включают себя следующее:
1. Неравенство:
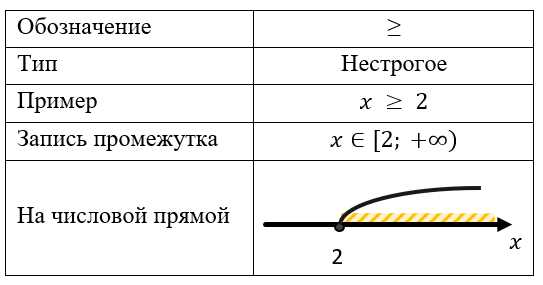
Неравенство — это выражение, указывающее на различие или отличие между двумя объектами. В математике мы обычно используем знаки неравенства, такие как «больше» (>), «меньше» (<), "больше или равно" (≥) и "меньше или равно" (≤), чтобы указать, какое число или выражение больше или меньше.
2. Знаки неравенства:
Знаки неравенства — это символы, которые мы используем для выражения неравенства между двумя числами или выражениями. Например, знак «>» означает «больше», а знак «<" означает "меньше".
3. Сравнение чисел:
Сравнение чисел — это процесс определения того, какое число больше или меньше другого. Когда мы сравниваем числа, мы используем знаки неравенства, чтобы указать, какое число больше или меньше.
4. Решение неравенств:
Решение неравенств — это процесс определения значений переменных, при которых неравенство является истинным. В математике мы можем использовать различные методы и стратегии для решения неравенств и нахождения их решений.
5. График неравенства:
График неравенства — это способ визуального представления неравенства на координатной плоскости. При графическом представлении неравенства мы используем линии и различные области на плоскости, чтобы показать, какие значения переменных удовлетворяют неравенству.
Все эти понятия важны для понимания математического неравенства и его применения в различных ситуациях. Они помогают нам не только сравнивать числа и выражения, но и решать сложные задачи, моделировать реальные ситуации и анализировать данные.
Простые неравенства
Простые неравенства — это неравенства, в которых участвуют только простые арифметические операции: сложение, вычитание, умножение и деление. Они представляют собой неравенства вида:
ax < b, ax > b, ax ≤ b, ax ≥ b
где a и b — числа, а x — неизвестная переменная. Кроме того, мы можем использовать простые неравенства для сравнения выражений:
ax + c < bx + d, ax + c > bx + d, ax + c ≤ bx + d, ax + c ≥ bx + d
где a, b, c и d — числа.
Итак, как решаются простые неравенства? Правила решения простых неравенств:
- Если неравенство имеет вид ax < b или ax > b, где a > 0, то правую часть делим на число a и меняем знак неравенства:
- Если неравенство имеет вид ax < b, то x > b/a.
- Если неравенство имеет вид ax > b, то x < b/a.
- Если неравенство имеет вид ax ≤ b или ax ≥ b, где a > 0, то правую часть делим на число a без изменения знака неравенства:
- Если неравенство имеет вид ax ≤ b, то x ≤ b/a.
- Если неравенство имеет вид ax ≥ b, то x ≥ b/a.
- Если неравенство имеет вид ax < b или ax > b, где a < 0, то правую часть делим на число a и меняем знак неравенства:
- Если неравенство имеет вид ax < b, то x < b/a.
- Если неравенство имеет вид ax > b, то x > b/a.
- Если неравенство имеет вид ax ≤ b или ax ≥ b, где a < 0, то правую часть делим на число a без изменения знака неравенства:
- Если неравенство имеет вид ax ≤ b, то x ≥ b/a.
- Если неравенство имеет вид ax ≥ b, то x ≤ b/a.
Применение этих правил позволяет нам находить решения простых неравенств и сравнивать числа и выражения. Разумеется, существует многосложные неравенства, для решения которых требуются дополнительные навыки и методы, но понимание и умение решать простые неравенства являются важной основой для работ с более сложными математическими задачами.
Теперь, когда у вас есть представление о простых неравенствах, вы можете начать исследовать их и применять их в различных ситуациях. Не стесняйтесь задавать себе вопросы о том, как эти неравенства могут быть применимы в вашей повседневной жизни или в других областях знаний. Учите математику с уверенностью и умением решать различные задачи, и она откроет перед вами множество возможностей.
Системы неравенств
В математике неравенства встречаются очень часто. Они используются для сравнения чисел или переменных. Но в некоторых случаях одно неравенство не может дать полную информацию о сравнении значений, и поэтому используются системы неравенств.
Система неравенств представляет собой совокупность двух или более неравенств, которые должны выполняться одновременно. В этом случае решение системы неравенств — это набор значений переменных, которые удовлетворяют всем неравенствам в системе.
Для решения систем неравенств необходимо использовать следующие правила:
- Если все неравенства в системе имеют одинаковый знак (например, все неравенства больше или все неравенства меньше), то нужно просто объединить их в одно неравенство. Например, система неравенств «x < 3" и "y < 5" может быть записана как "x < 3 и y < 5".
- Если неравенства имеют разные знаки, то нужно использовать операции объединения или пересечения интервалов. Например, система неравенств «x > 2» и «y < 4" может быть записана как "x > 2 или y < 4". В этом случае решением системы будут все значения, которые удовлетворяют хотя бы одному из неравенств.
- Если система состоит из трех или более неравенств, то нужно использовать методы графического представления или алгоритмы для нахождения всех возможных значений переменных.
Решение системы неравенств может быть представлено в виде неравенств, характеризующих диапазон значений переменных. Например, система неравенств «x > 2» и «x < 5" имеет решение "2 < x < 5".
Системы неравенств находят свое применение в реальной жизни. Например, они используются для ограничения допустимого диапазона значений в задачах оптимизации или планирования.
На самом деле, системы неравенств — это очень мощный инструмент в математике, который позволяет анализировать и сравнивать несколько переменных одновременно. Их решение требует логического мышления и умения работать с неравенствами. Но с практикой и опытом они становятся все проще и понятнее.
Определение функции

Чтобы лучше понять, что такое функция, представь себе, что ты повар и у тебя есть список рецептов и список ингредиентов. Ты можешь использовать рецепты, чтобы приготовить различные блюда из имеющихся ингредиентов. В этом случае, список рецептов является первым множеством (входными данными), а список ингредиентов — вторым множеством (выходными данными).
В математике, функция обозначается с помощью буквы f (или любой другой буквы) и записывается следующим образом: f(x). Здесь x — это переменная, которая принимает значения из первого множества, а f(x) — это значение функции, которое соответствует данному значению переменной x. Это можно представить в виде таблицы или графика.
Например, представь, что у нас есть функция f(x) = 2x. В этом случае, значение функции f(x) будет всегда в два раза больше значения переменной x. Если x = 3, то f(x) = 2 * 3 = 6. Если x = 5, то f(x) = 2 * 5 = 10. Здесь переменная x представляет первое множество (входные данные), а значение функции f(x) представляет второе множество (выходные данные).
Важно отметить, что для каждого значения переменной x должно быть однозначно определено значение функции f(x). Нельзя иметь ситуацию, когда одному значению переменной x соответствуют различные значения функции.
Функции представляют собой мощный инструмент в математике, который позволяет моделировать и анализировать различные явления и отношения. Они имеют широкий спектр применений в науке, технологии, экономике и других областях. Вместе с тем, понимание функций поможет тебе лучше разбираться в математике и находить решения для различных проблем.
Итак, функция — это связь между двумя множествами, которая позволяет нам предсказывать или вычислять значения второго множества на основе известных значений первого множества. Представь себе функцию, как повар, который использует рецепты, чтобы приготовить блюда из имеющихся ингредиентов. Используйте функции, чтобы моделировать и анализировать различные явления и отношения в математике и в реальном мире. Развивай свои навыки работы с функциями, и они откроют перед тобой новые возможности в познании и решении математических проблем.
Неравенства с переменными
Неравенства с переменными играют важную роль в математике, так как позволяют моделировать реальные ситуации. Они помогают нам решать различные задачи, такие как определение диапазонов значений переменной или нахождение условий, при которых определенное соотношение будет истинно.
Для записи неравенств мы используем математические символы, такие как «>» (больше), «<" (меньше), ">=» (больше или равно), «<=" (меньше или равно), и иногда "≠" (не равно). В качестве переменных мы часто используем буквы, такие как x, y или z.
Давайте рассмотрим пример неравенства с переменными:
2x + 5 > 10
Это неравенство говорит нам, что результат умножения переменной x на 2 и последующему прибавлению 5 должен быть больше 10. Для решения этого неравенства, мы должны найти диапазон значений переменной x, где неравенство будет истинным.
Чтобы решить эту неравенству, мы должны сначала избавиться от 5, вычтя его из обеих сторон. Это даст нам:
2x > 5
Затем мы делим обе стороны на 2, чтобы найти значение переменной x:
x > 2.5
Таким образом, переменная x должна быть больше 2.5, чтобы неравенство было истинным. Мы можем представить это в виде диапазона значений: x ∈ (2.5, +∞).
Неравенства с переменными позволяют нам моделировать и анализировать различные ситуации в математике и реальной жизни. Они помогают нам определить условия, при которых определенное соотношение выполняется, и находить диапазоны значений переменных. Умение работать с неравенствами с переменными не только расширяет наши знания в математике, но и развивает наше логическое мышление и аналитические навыки.
Неравенство в математике: правила и определение

Правила неравенств:
- Если к обеим частям неравенства прибавить или вычесть одно и то же число, то знак неравенства остается неизменным.
- Если обе части неравенства умножить или разделить на положительное число, то знак неравенства остается неизменным.
- Если обе части неравенства умножить или разделить на отрицательное число, то знак неравенства меняется.
- Если к обеим частям неравенства применить отрицание, то знак неравенства меняется на противоположный.
Например:
- Если из неравенства 2x > 6 вычесть 4, получим 2x — 4 > 2. Знак неравенства остается неизменным.
- Если обе части неравенства 3x ≤ 9 разделить на 3, получим x ≤ 3. Знак неравенства остается неизменным.
- Если обе части неравенства -5x ≥ 10 умножить на -1, получим 5x ≤ -10. Знак неравенства меняется.
- Если к обеим частям неравенства x + 3 ≤ 7 применить отрицание, получим -x — 3 ≥ -7. Знак неравенства меняется на противоположный.
Неравенство можно решать и графически, используя координатную плоскость. В таком случае, каждая сторона неравенства представляет собой определенную область на плоскости. Пересечение этих областей указывает на интервалы, удовлетворяющие заданному неравенству.