В математике нумерация является одним из важнейших навыков, которым должны овладеть учащиеся начальной школы. Она помогает детям ориентироваться в числовых значениях и правильно записывать числа. В этом возрасте дети начинают изучать разрядность чисел, используя сотни, десятки и единицы. Нумерация также включает в себя правила записи чисел, как с пробелами, так и без них, а также правила чтения чисел по слогам. Важно научиться правильно располагать цифры в числе и понимать их значимость в разряде. Знания по нумерации являются основой для изучения десятичной системы счисления и более сложных математических операций.
Основные понятия в нумерации
Первое, что мы должны знать о нумерации, это порядковые числительные. Они помогают нам указать, в каком порядке находится объект или событие. Например, мы можем говорить: «Сегодня у нас третий урок» или «Ответь на вопрос номер пять». Они помогают нам ориентироваться и понимать, что происходит в определенный момент времени.
В нумерации также применяются порядковые числа. Они показывают положение числа в системе нумерации. Например, мы можем говорить: «Первый класс идет до второго класса», «У меня самая большая третья кукла в коллекции». Они помогают нам дать объектам уникальные идентификаторы и определить их место в ряду.
Важным понятием в нумерации является разрядность числа. Разрядность указывает на количество цифр в числе. Например, в числе 2432 разрядность равна четырем, так как есть четыре цифры. Разрядность числа имеет большое значение при выполнении различных математических операций, таких как сложение, вычитание, умножение и деление.
Все эти понятия очень важны, чтобы быть в состоянии понимать и использовать систему нумерации. Они помогут вам в повседневной жизни, в школе и даже в математике. Знание нумерации также поможет вам почувствовать уверенность и самостоятельность в мире чисел.
Вам интересно нумерация? Что еще бы вы хотели узнать о ней? Какие вопросы у вас возникают? Напишите в комментариях, и мы обязательно ответим на них!
Число и цифра

Давай начнем с числа. Число — это абстрактное математическое понятие, которое используется для измерения, подсчета и сравнения. Числа помогают нам описывать количество или порядок объектов вокруг нас. Например, сколько яблок у тебя в корзине или какое число мест в автобусе.
Цифры, с другой стороны, это символы, которые представляют числа. Они используются для записи чисел и обобщенно называются цифрами, хотя на самом деле цифра — это только одна из цифровых символов.
Представь себе, что видишь на доске числовую запись «368». Как ты думаешь, что это — число или цифра? Правильно, это число! А теперь рассмотри это число подробнее. Каждая из цифр 3, 6 и 8 является цифрой, которая помогает нам записать число 368. Таким образом, число состоит из цифр. Понятно?
Теперь давай поговорим о базовых понятиях, связанных с числами и цифрами. Есть несколько важных терминов, которые помогут нам лучше понять, как работают числа и цифры:
- Разряд — это позиция, занимаемая цифрой в числе. Каждая цифра в числе имеет свое значение в зависимости от разряда.
- Цифровое значение — это значение, которое придается цифре в зависимости от ее разряда. К примеру, цифра 3 в числе 368 имеет значение 300, так как она находится в сотнях.
- Порядок — это позиция, в которой находится число относительно других чисел. Например, число 368 стоит между числами 367 и 369.
Теперь, когда мы разобрались с основными понятиями, можешь попробовать самостоятельно собрать число, используя цифры. Например, скажи, какое число получится, если сложить цифры 5 и 7?
Важно понимать, что числа и цифры — это не только математические понятия, но и часть нашей повседневной жизни. Мы видим и используем числа и цифры в разных ситуациях: когда записываем свой возраст, когда звоним по телефону или когда читаем время на часах.
Таким образом, понимание чисел и цифр поможет нам лучше разбираться в окружающем мире и решать различные задачи. А сейчас самое время потренироваться и поиграть с числами и цифрами!
Разряды чисел
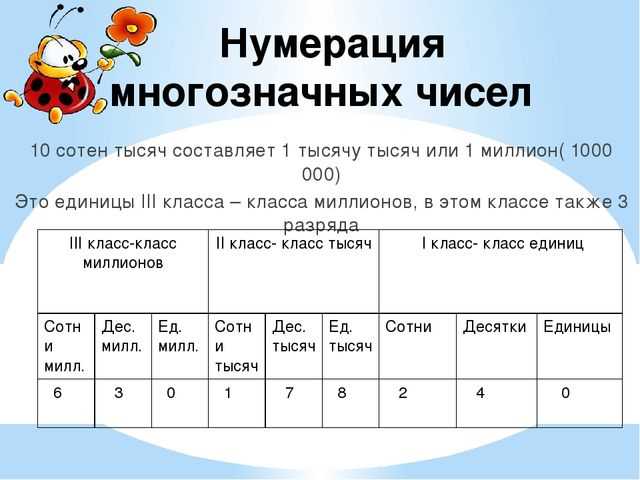
Разряды чисел — это способ организации и представления чисел с помощью позиционной системы счисления. В позиционной системе каждая позиция цифры в числе имеет определенное значение в зависимости от разряда, которому она принадлежит.
Давайте рассмотрим пример числа 456. В этом числе есть три разряда: сотни, десятки и единицы. Значение каждого разряда зависит от его позиции. Так, цифра 4 находится в разряде сотен, поэтому она имеет значение 400. Цифра 5 находится в разряде десятков и имеет значение 50. И наконец, цифра 6 находится в разряде единиц и имеет значение 6. Сложив эти значения, мы получим число 456.
Разряды чисел помогают нам упорядочить и легче понять числа. Они также помогают нам выполнять арифметические операции, такие как сложение, вычитание, умножение и деление. Например, при сложении двух чисел, мы складываем разряды по одному, начиная с самого младшего разряда.
| Разряд | Значение |
|---|---|
| Тысячи | 1000 |
| Сотни | 100 |
| Десятки | 10 |
| Единицы | 1 |
Разряды чисел также помогают нам сравнивать и упорядочивать числа. Например, если у нас есть два числа: 123 и 456, мы можем сравнить их, начиная с самого старшего разряда. В данном случае 4 > 1, поэтому число 456 больше числа 123.
Понимание разрядов чисел является важным навыком, который поможет в дальнейшем изучении математики и решении различных задач. Надеюсь, вы сейчас лучше понимаете, что такое разряды чисел и как они помогают нам работать с числами. Что вы думаете о разрядах чисел? Как они помогают вам в понимании математики? Делитесь своим мнением в комментариях!
Целые числа

Добро пожаловать в мир целых чисел! Здесь мы с вами будем исследовать основные понятия и правила, связанные с целыми числами, а также разберемся, как с ними работать.
Целые числа – это числа без дробной части. Они могут быть как положительными, так и отрицательными. Все они можно представить на числовой прямой, где положительные числа находятся справа от нуля, а отрицательные – слева. Ноль находится в центре.
Наверное, ты уже знаком с понятием «число», но а теперь представь, что вместо слова «число» мы говорим «целое число». Если я скажу «У Лены есть 5 яблок», это будет обычное число, ты не будешь думать о целых числах. Но если я скажу «У Лены было 5 минут до этого», тогда ты может представить себе, что это целое число. Ты понимаешь разницу? Второй пример связан с временем, а оно всегда измеряется в целых числах.
Теперь давай посмотрим, как работать с целыми числами.
Сложение целых чисел
Когда нужно сложить два целых числа, мы складываем их по модулю (то есть не учитываем знак) и прибавляем знак числа с большим по модулю значением. Например, (-5) + (-3) = -8, а 4 + (-2) = 2.
Вычитание целых чисел
Вычитание целых чисел – это противоположная операция сложению. Если нужно вычесть одно число из другого, то добавляем обратное число и выполняем сложение. Например, 7 — 3 = 7 + (-3) = 4, а (-5) — (-3) = (-5) + 3 = -2.
Умножение целых чисел
При умножении двух целых чисел, результат будет иметь тот же знак, что и сомножители. Например, (-2) * 3 = -6, а (-4) * (-2) = 8.
Деление целых чисел
При делении двух целых чисел, результат может быть целым числом или десятичной дробью. Если результат – целое число, то его знак такой же, как и у делимого. Например, 10 / 2 = 5, а (-15) / (-3) = 5.
Также есть случаи, когда при делении одного целого числа на другое получается неполное частное, например, 7 / 2 = 3 (остаток 1).
Теперь у тебя есть общее представление о целых числах и основных операциях с ними. Ты готов к дальнейшей работе с целыми числами и решению математических задач. Запомни основные правила и не бойся экспериментировать!
Десятичная система счисления
Давайте рассмотрим пример: число 642. В этом числе цифра 6 находится в позиции с весом 100, цифра 4 находится в позиции с весом 10, а цифра 2 находится в позиции с весом 1. Чтобы вычислить значение числа, мы умножаем каждую цифру на соответствующий вес и складываем полученные произведения: 6 * 100 + 4 * 10 + 2 * 1 = 600 + 40 + 2 = 642.
Десятичная система счисления проста и удобна для повседневного использования. Мы привыкли к ней и используем ее для счета денег, измерения времени и многих других вещей. Кроме того, десятичная система позволяет нам легко сравнивать числа и выполнять арифметические операции, такие как сложение, вычитание, умножение и деление.
Чтобы лучше понять десятичную систему счисления, давайте рассмотрим пример числа 5678. Каждая цифра в этом числе имеет свое значение: цифра 5 находится в позиции тысяч, цифра 6 находится в позиции сотен, цифра 7 находится в позиции десятков, и цифра 8 находится в позиции единиц. Можно сказать, что число 5678 состоит из пяти тысяч, шестисот семидесяти восьми десятков и восьми единиц.
Теперь, когда мы знаем основные понятия и правила десятичной системы счисления, давайте попробуем решить несколько задач, чтобы еще больше укрепить наши знания и навыки математики!
Сравнение чисел
Когда мы сравниваем числа, мы выясняем, какое число больше, а какое меньше. Для этого используются специальные знаки: знак больше ( > ), знак меньше ( < ) и знак равно ( = ).
Давайте рассмотрим несколько примеров, чтобы лучше разобраться. Представьте, у вас есть два числа: 5 и 7. Какое из них больше? Если вы сказали, что 7 больше, то вы правильно сравнили числа. Мы можем записать это так: 5 < 7 или 7 > 5. Знак «<" означает "меньше", а знак ">» означает «больше».
А что если у нас есть два числа, которые одинаковы? Например, 2 и 2. В этом случае мы будем использовать знак равенства «=». Мы можем записать это так: 2 = 2. Это означает, что оба числа равны друг другу.
Теперь давайте потренируемся. Вот вам несколько пар чисел. Попробуйте сравнить их и записать правильное сравнение с помощью знаков больше ( > ), меньше ( < ) и равно ( = ):
- 10 и 5
- 3 и 3
- 8 и 12
- 6 и 6
Отлично! Проверьте свои ответы и посмотрите, справились ли вы.
Важно помнить, что сравнение чисел — это одно из основных понятий в математике. Оно помогает нам понять, какие числа больше или меньше. Зная правила сравнения, мы можем решать различные задачи и проблемы.
Так что продолжайте тренироваться и развиваться! Математика — увлекательная и полезная наука, которая помогает нам понять мир вокруг нас.
Нумерация в математике для 4 класса: основные понятия и правила
В математике для 4 класса нумерация играет важную роль. Она используется для обозначения порядка элементов, позиции объектов и решения различных задач.
Основные понятия и правила нумерации:
- Целые числа образуют бесконечную последовательность, включающую в себя положительные и отрицательные числа, а также ноль.
- Натуральные числа — это целые положительные числа, начиная с единицы.
- Упорядоченная нумерация — это нумерация, в которой элементы упорядочены по возрастанию или убыванию.
- Однозначная нумерация — это нумерация, в которой каждый элемент имеет уникальный номер.
- Двоичная система — это система нумерации, основанная на использовании двух цифр: 0 и 1.
Правила нумерации:
- Порядок нумерации — правило, указывающее на последовательность нумерации элементов: от меньшего к большему или от большего к меньшему.
- Основание системы счисления — это количество цифр, которые используются для записи чисел в данной системе. Для десятичной системы счисления основание равно 10, а для двоичной системы — 2.
- Разрядность числа — это число позиций, которые занимает число в нумерации. Например, в десятичной системе счисления число 123 имеет разрядность 3.
- Правило нулевого разряда — в некоторых системах счисления нулевой разряд может быть занят нулем, что позволяет использовать больше цифр для записи чисел.