Объединение множеств в математике: понятие и примеры

Когда мы говорим об объединении множеств, мы имеем в виду операцию, которая позволяет нам создавать новое множество, состоящее из элементов двух или более заданных множеств. Это важное понятие в математике, которое помогает нам работать с множествами и их элементами.

Примером объединения множеств может служить ситуация, когда у нас есть множество A, состоящее из всех четных чисел, и множество B, состоящее из всех нечетных чисел. Объединение этих двух множеств даст нам новое множество, содержащее все числа, как четные, так и нечетные.

Операция объединения множеств имеет важное значение в различных областях математики, включая теорию множеств, логику и алгебру. Она позволяет нам совершать различные операции с множествами и решать сложные задачи.

Что такое объединение множеств?

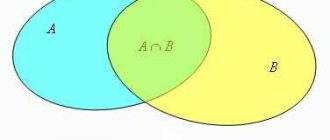
Чтобы понять суть объединения, представь себе два множества — множество фруктов и множество овощей. Множество фруктов включает яблоки, груши и бананы, а множество овощей — морковь, помидоры и картофель. Если мы объединим эти два множества, то получим новое множество, включающее все элементы обоих исходных множеств. То есть в объединенном множестве будут присутствовать яблоки, груши, бананы, морковь, помидоры и картофель.

Объединение множеств обозначается символом «∪». Для объединения множеств А и В запись будет выглядеть вот так: A ∪ B. Или можно сказать «множество А объединено с множеством В».

Однако важно отметить, что при объединении множеств не происходит дублирования элементов. Если в одном из исходных множеств есть элементы, которые уже присутствуют в другом множестве, то они будут учтены только один раз в объединенном множестве. Например, если в множестве фруктов также содержатся яблоки, которые уже есть в множестве овощей, то в объединенном множестве будет только одно «яблоко».

Объединение множеств является важной операцией в математике, так как позволяет совмещать различные коллекции элементов и работать с ними как с единым целым. Например, в дискретной математике, объединение множеств используется для нахождения идентичности элементов или создания новых коллекций данных.

Таким образом, объединение множеств — это способ собрать все элементы из двух или более множеств и объединить их в одно множество, сохраняя уникальность элементов.

Примеры объединения множеств

Обратите внимание, что элементы внутри объединенного множества могут быть упорядочены или неупорядочены. Они также могут быть повторяющимися или уникальными, в зависимости от того, встречаются ли они в исходных множествах несколько раз или только один раз.

Пример 1: Объединение множеств чисел

Представим у нас есть два множества чисел: A = {1, 2, 3} и B = {3, 4, 5}. Чтобы найти объединение этих двух множеств, мы берем все элементы из обоих множеств и исключаем дубликаты. Таким образом, объединение множеств A и B будет: A ∪ B = {1, 2, 3, 4, 5}.

Пример 2: Объединение множеств слов

Предположим, у вас есть два множества слов: C = {«яблоко», «банан», «груша»} и D = {«груша», «апельсин», «слива»}. Чтобы найти объединение этих двух множеств, мы берем все слова из обоих множеств и удаляем повторяющиеся слова. Таким образом, объединение множеств C и D будет: C ∪ D = {«яблоко», «банан», «груша», «апельсин», «слива»}.

Пример 3: Объединение множеств фруктов и овощей

Рассмотрим еще один пример, где мы имеем два множества, но уже с разными типами элементов. Пусть у нас будет множество фруктов E = {«яблоко», «банан», «груша»} и множество овощей F = {«морковь», «кукуруза», «груша»}. Чтобы найти объединение этих двух множеств, мы берем все элементы из обоих множеств и исключаем дубликаты. Таким образом, объединение множеств E и F будет: E ∪ F = {«яблоко», «банан», «груша», «морковь», «кукуруза»}.

Пример 4: Объединение пустого множества с другим множеством

Важно отметить, что объединение пустого множества с другим множеством не изменяет этого другого множества. Например, если у нас есть множество G = {} (пустое множество) и множество H = {1, 2, 3}, то объединение множеств G и H будет равно множеству H: G ∪ H = {1, 2, 3}.

Таким образом, объединение множеств позволяет нам объединить элементы из разных множеств в одно множество, исключая при этом повторяющиеся элементы. Эта операция широко используется в математике и других областях для объединения данных и упрощения их обработки.

Свойства объединения множеств

1. Коммутативность

Одним из основных свойств объединения множеств является его коммутативность. Это означает, что порядок объединяемых множеств не имеет значения. Например, объединение множеств A и B будет равно объединению множеств B и A.

Пример: A ∪ B = B ∪ A

2. Ассоциативность

Еще одно важное свойство объединения множеств — его ассоциативность. Это означает, что при объединении трех или более множеств порядок объединения не имеет значения. Например, объединение множеств A, B и C будет одинаково, независимо от порядка объединения.

Пример: (A ∪ B) ∪ C = A ∪ (B ∪ C)

3. Идемпотентность

Идемпотентность — еще одно важное свойство объединения множеств. Оно означает, что повторное объединение множества с самим собой не изменяет его. Другими словами, если A — множество, то объединение A снова с собой даст тот же результат.

Пример: A ∪ A = A

4. Распределительное свойство относительно пересечения

Одно из полезных свойств объединения множеств — его распределительное свойство относительно пересечения. Это означает, что объединение двух множеств, взятое с пересечением третьего множества, равно объединению каждого из множеств, взятому с пересечением с третьим множеством.

Пример: A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)

5. Нейтральный элемент

Объединение множеств имеет нейтральный элемент, который не влияет на результат. Это пустое множество, которое не содержит никаких элементов. Если объединить множество с пустым множеством, результатом будет само это множество.

Пример: A ∪ ∅ = A

6. Закон Де Моргана

Закон Де Моргана — это особое свойство объединения множеств, которое связывает его с операцией дополнения. Он гласит, что дополнение объединения двух множеств равно пересечению дополнений этих множеств.

Пример: (A ∪ B)’ = A’ ∩ B’

Все эти свойства объединения множеств играют важную роль в математике. Они позволяют нам анализировать и решать различные задачи, используя операцию объединения множеств. Таким образом, понимание этих свойств является важным шагом в обучении математике и решении проблем.

Операции с объединением множеств

Давайте рассмотрим примеры, чтобы более понятно представить операцию объединения множеств. Предположим, у нас есть два множества:

A = {1, 2, 3}

B = {3, 4, 5}

Операция объединения позволяет нам объединить все элементы из множества A и B. Применив операцию объединения, мы получим новое множество, содержащее следующие элементы:

A ∪ B = {1, 2, 3, 4, 5}

Как видите, все элементы из множества A и B были объединены в одно множество.

Обратите внимание, что в результирующем множестве каждый элемент появляется только один раз. Например, в множестве A = {1, 2, 3} элемент «3» появляется только один раз, и он также появляется только один раз в множестве B = {3, 4, 5}. Поэтому, когда мы объединяем множества, элемент «3» появляется только один раз в объединенном множестве A ∪ B = {1, 2, 3, 4, 5}.

Операция объединения множеств может применяться не только к двум множествам, но и к любому количеству множеств. Например, если у нас есть три множества:

C = {2, 3, 4}

D = {4, 5, 6}

E = {6, 7, 8}

И если мы применим операцию объединения к этим трем множествам, мы получим новое множество, содержащее все элементы из C, D и E:

C ∪ D ∪ E = {2, 3, 4, 5, 6, 7, 8}

Таким образом, операция объединения множеств позволяет нам объединять все элементы из нескольких множеств в одно множество и удалять повторяющиеся элементы.

Использование операции объединения множеств в математике может быть полезным во многих областях, например, в теории множеств, логике, алгебре и дискретной математике. Она позволяет нам упростить задачи, объединить данные и выделить общие элементы.

Объединение множеств в математике: понятие и примеры

В математике, объединение двух или более множеств происходит путем объединения всех их элементов, исключая повторяющиеся значения. Результатом объединения будет новое множество, которое содержит все уникальные элементы из исходных множеств.

Обозначение объединения двух множеств A и B выглядит следующим образом: A ∪ B. В некоторых случаях, когда нужно объединить более двух множеств, можно использовать более длинное выражение, например: A ∪ B ∪ C.

Примеры объединения множеств:

• Пусть A = {1, 2, 3} и B = {3, 4, 5}. Тогда A ∪ B = {1, 2, 3, 4, 5}.
• Пусть C = {apple, orange} и D = {banana, apple}. Тогда C ∪ D = {apple, orange, banana}.

Объединение множеств позволяет объединить элементы из различных множеств в одно множество, что может быть полезно при решении математических задач или анализе данных. Это важная операция в теории множеств и широко используется в различных областях математики и информатики.