Когда решаем задачи в математике, часто необходимо объединять различные элементы или наборы в один, чтобы получить более удобное представление или решение. Это понятие объединения является важным инструментом в математическом анализе и алгебре.
Объединение позволяет нам работать с множествами и группировать элементы в более общие категории. Основные принципы объединения включают поиск общих элементов в двух или более множествах и создание нового множества, содержащего все элементы из исходных множеств.
Понимание и использование понятия объединения помогает нам решать сложные задачи, анализировать данные и строить логические модели. Это важный инструмент, который помогает нам упростить и структурировать нашу работу в математике.
Раздел 1: Введение в понятие объединения в математике
Итак, допустим, у тебя есть множество А, состоящее из элементов «яблоко», «банан», «апельсин», и множество Б, состоящее из элементов «манго», «киви», «груша». Твоя задача – создать новое множество, которое будет содержать все элементы обоих множеств. Это и есть объединение множеств А и Б.
Представь себе, что каждое множество – это группа твоих друзей. Множество А – это группа твоих школьных друзей, и множество Б – это группа твоих соседских друзей. И ты решил объединить эти две группы в одну, чтобы у тебя была одна большая и веселая компания. Вот именно это мы делаем с множествами в математике.
Обрати внимание, что элементы нового множества не повторяются. То есть, если в обоих множествах содержится одинаковый элемент, то он будет добавлен в объединение только один раз. Давай посмотрим на примере:
Множество А: «яблоко», «банан», «апельсин»
Множество Б: «манго», «киви», «груша», «яблоко»
Объединение множеств А и Б будет выглядеть следующим образом:
Объединение А и Б: «яблоко», «банан», «апельсин», «манго», «киви», «груша»
Здорово, правда? Ты объединил две разные группы друзей в одну большую и разнообразную компанию.
А что, если одно из множеств будет пустым? Подумай об этом. Как ты думаешь, будет ли что-то измениться? Например, если множество А пустое, а множество Б содержит элементы, какое будет объединение? Давай разбираться!
Оказывается, если одно из множеств пустое, то объединение будет просто равно другому множеству. Возвращаясь к нашим друзьям, это как если бы ты пытался объединить свою группу школьных друзей со свеженькой группой твоих соседей, а в результате получаешь только саму группу соседей. У тебя остались только новые друзья, но ничего не произошло с твоей школьной компанией. Так и в математике – объединение пустого множества со вторым множеством не приводит к каким-либо изменениям второго множества.
Итак, вот тебе основная идея объединения в математике – создание нового множества, которое объединяет элементы из двух разных множеств. Оно великолепно работает, когда тебе нужно собрать вместе различные группы либо элементы для создания чего-то нового и уникального.
Думаешь, ты смог бы применить понятие объединения в своей повседневной жизни? Какими группами или элементами ты бы хотел объединиться? Задай себе этот вопрос и подумай об этом. Математика всегда готова помочь нам в объединении и создании новых идей и возможностей!
Определение объединения
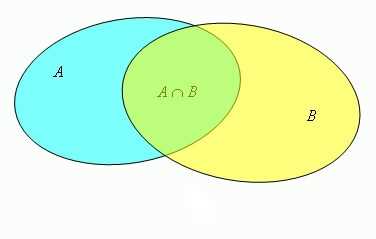
В математике объединение означает соединение двух или более множеств для образования нового множества, которое содержит все элементы из исходных множеств. В результате объединения мы получаем большее множество, которое включает все элементы из исходных множеств, без повторов.
Давайте рассмотрим пример. Представьте, что у нас есть два множества:
- Множество A: {1, 2, 3}
- Множество B: {3, 4, 5}
Мы можем объединить эти два множества, чтобы получить новое множество, которое будет содержать все элементы из обоих исходных множеств. В результате объединения множеств A и B получим:
Объединение A и B: {1, 2, 3, 4, 5}
Обратите внимание, что элемент 3 включен только один раз в объединении, даже если он присутствует в обоих исходных множествах. Это потому, что в объединении мы не дублируем элементы. Мы берем каждый элемент только один раз.
Объединение — это простой, но важный математический принцип, который находит свое применение в разных областях знаний. Он позволяет нам комбинировать различные идеи и концепции, чтобы создавать что-то новое и расширять наше понимание мира.
Раздел 2
Мы уже поговорили о том, что такое объединение в математике и в каких случаях его используют. Теперь перейдем к следующему разделу нашего разговора и рассмотрим основные принципы объединения.
Основным принципом объединения в математике является то, что два или более множества объединяются в одно большое множество путем соединения их элементов. Таким образом, объединение представляет собой процесс сбора всех элементов из исходных множеств без повторений.
Давайте рассмотрим простой пример, чтобы лучше понять, как работает объединение. Предположим, у нас есть два множества: А = {1, 2, 3} и В = {3, 4, 5}. Чтобы объединить эти два множества в одно, нам нужно взять все элементы из обоих множеств и поместить их в новое множество без повторений. В результате получим множество С = {1, 2, 3, 4, 5}.
Однако стоит отметить, что при объединении множеств может возникнуть ситуация, когда в исходных множествах есть одинаковые элементы. В таком случае, в результирующем множестве они будут представлены только один раз. Например, если у нас есть два множества: А = {1, 2, 3, 4} и В = {3, 4, 5, 6}, то в результате их объединения получим множество С = {1, 2, 3, 4, 5, 6}.
Также важно отметить, что объединение является коммутативной операцией, что означает, что порядок, в котором мы объединяем множества, не влияет на результат. То есть, объединение множеств А и В будет равно объединению множеств В и А. Например, если у нас есть множество А = {1, 2, 3} и множество В = {3, 4, 5}, то А объединено с В будет равно В объединено с А, то есть множество С = {1, 2, 3, 4, 5} получится как результат в обоих случаях.
В процессе объединения множеств мы можем использовать различные операции, такие как пересечение и разность, чтобы получить более точные результаты. Например, можно найти пересечение двух множеств, которое будет содержать только элементы, присутствующие в обоих множествах одновременно.
Итак, мы рассмотрели основные принципы объединения в математике. Теперь вы должны иметь более четкое представление о том, как происходит объединение множеств и какие принципы ему лежат в основе. В следующем разделе мы поговорим о том, как применять эти принципы на практике и решать задачи с использованием объединения.
Основные свойства объединения

Первое свойство объединения — это коммутативность. Это значит, что порядок объединяемых множеств не имеет значения. Например, если мы объединяем множества А и В, то результат будет таким же, как если бы мы объединяли множества В и А. Например, объединение множеств {1, 2, 3} и {4, 5} будет выглядеть так: {1, 2, 3, 4, 5}. А объединение множеств {4, 5} и {1, 2, 3} будет выглядеть также: {1, 2, 3, 4, 5}.
Второе свойство объединения — это ассоциативность. Это значит, что при объединении трех или более множеств порядок их объединения не имеет значения. Например, если мы объединяем множества А, В и С, то результат будет таким же, как если бы мы сначала объединили множества А и В, а затем объединили результат с множеством С. Например, объединение множеств {1, 2} и {3, 4}, а затем с множеством {5, 6}, будет выглядеть так: {1, 2, 3, 4, 5, 6}. А объединение множеств {1, 2} с объединением множеств {3, 4} и {5, 6} будет также: {1, 2, 3, 4, 5, 6}.
Третье свойство объединения связано с понятием пустого множества. Пустое множество не содержит ни одного элемента. Когда мы объединяем пустое множество с любым другим множеством, результатом будет то же самое множество без изменений. Например, объединение пустого множества с множеством {1, 2, 3} будет выглядеть так: {1, 2, 3}. А объединение пустого множества с пустым множеством будет пустым множеством: {}.
И последнее свойство, о котором я хотел бы рассказать, — это дистрибутивность объединения относительно пересечения. Это свойство означает, что объединение двух множеств, пересекаемых третьим множеством, эквивалентно объединению каждого из множеств с пересечением третьего множества. Например, объединение множеств {1, 2} и {2, 3}, пересекаемых множеством {2}, будет выглядеть так: {1, 2, 3}. А объединение множеств {1, 2} с пересечением множеств {2} и {2, 3} будет также: {1, 2, 3}.
Итак, основные свойства объединения — коммутативность, ассоциативность, пустое множество и дистрибутивность относительно пересечения. Знание этих свойств помогает нам лучше понимать и работать с объединением множеств в математике. Каждое из этих свойств имеет свою важность и применение в различных областях науки и повседневной жизни. Надеюсь, я смог помочь вам лучше понять это понятие и его основные принципы!
Раздел 3
В предыдущих разделах мы уже узнали, что такое объединение и какие принципы его использования существуют. Теперь давайте поговорим о третьем разделе, где мы рассмотрим некоторые особенности объединения в математике.
Во-первых, объединение является одним из основных операторов в множественных операциях. Оно позволяет компоновать два или более множества в одно, сохраняя все элементы каждого из них. Например, если у нас есть множество A = {1, 2, 3} и множество B = {3, 4, 5}, то объединение множеств A и B будет выглядеть как A ∪ B = {1, 2, 3, 4, 5}.
Во-вторых, объединение может быть использовано для определения отношений между различными множествами. Например, если у нас есть множество X = {яблоко, апельсин, банан} и множество Y = {красный, оранжевый, желтый}, мы можем определить отношение «иметь цвет» (X имеет цвет Y) с помощью объединения этих двух множеств. Таким образом, мы можем создать множество отношений R = {(яблоко, красный), (яблоко, оранжевый), (яблоко, желтый), (апельсин, красный), (апельсин, оранжевый), (апельсин, желтый), (банан, красный), (банан, оранжевый), (банан, желтый)}.
В-третьих, объединение может быть использовано для решения сложных задач, требующих комбинации информации из различных источников. Например, представьте, что у нас есть два множества людей: A — люди, которые любят спорт, и B — люди, которые умеют играть на музыкальных инструментах. Если мы объединим эти два множества, то получим новое множество C — люди, которые и любят спорт, и умеют играть на музыкальных инструментах.
Итак, мы рассмотрели несколько особенностей объединения в математике. Оно позволяет комбинировать множества, определять отношения между ними и решать сложные задачи. Открытым остается вопрос: как мы можем применить эти знания в повседневной жизни? Возможно, вы уже нашли несколько примеров, где объединение множеств может помочь вам получить новые знания или решить задачу. Поделитесь ими с нами!
Примеры объединения
-
Пример 1:
Представим, что у нас есть два множества:
- Множество А: {1, 2, 3}
- Множество В: {3, 4, 5}
Чтобы найти объединение данных множеств, мы просто объединяем все элементы в новое множество:
- Объединение А и В: {1, 2, 3, 4, 5}
Таким образом, мы получаем новое множество, состоящее из всех уникальных элементов множеств А и В.
-
Пример 2:
Представим, что у нас есть два множества:
- Множество А: {яблоко, груша, вишня}
- Множество В: {вишня, апельсин, банан}
Объединение этих множеств даст нам новое множество:
- Объединение А и В: {яблоко, груша, вишня, апельсин, банан}
Таким образом, мы создаем новое множество, содержащее все уникальные фрукты из множеств А и В.
-
Пример 3:
Представим, что у нас есть три множества:
- Множество А: {красный, синий, зеленый}
- Множество В: {желтый, голубой}
- Множество С: {оранжевый, фиолетовый}
Чтобы найти объединение всех трех множеств, мы просто объединяем их все в одно множество:
- Объединение А, В и С: {красный, синий, зеленый, желтый, голубой, оранжевый, фиолетовый}
Таким образом, мы получаем новое множество, содержащее все уникальные цвета из множеств А, В и С.
Это лишь несколько примеров, которые помогут вам понять принцип объединения в математике. Объединение является важной операцией, которая позволяет комбинировать элементы из разных множеств и создавать новые множества. Это основной инструмент, который помогает в решении различных математических задач и проблем.
Объединение в математике: понятие и основные принципы

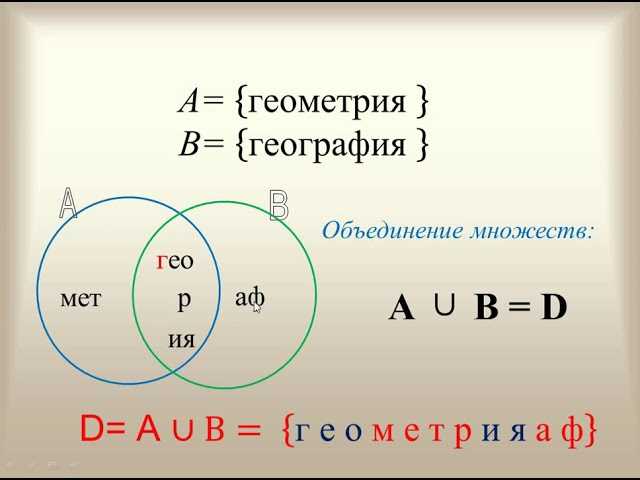
Основным символом для обозначения объединения является символ «∪». Если А и В — два множества, то их объединение обозначается как А∪В и состоит из всех элементов, которые принадлежат хотя бы одному из этих множеств.
Основные принципы объединения множеств:
- Объединение множеств коммутативно: А∪В = В∪А. Порядок множеств, которые объединяются, не имеет значения.
- Объединение множеств ассоциативно: (А∪В)∪С = А∪(В∪С). Порядок объединения множеств не влияет на результат.
- Множество объединения содержит все элементы исходных множеств без повторений. Если элемент принадлежит обоим множествам, он включается в объединение только один раз.
Объединение множеств широко используется в различных областях математики и ее приложениях. Например, в теории множеств оно используется для определения пересечения, разности и симметрической разности множеств. Также оно применяется в теории вероятностей при объединении событий, в алгебре логики и других математических дисциплинах.