Здравствуйте, друзья! Сегодня хочу поговорить с вами о концепции объема в логике и его применении. Знание этого понятия играет важную роль в осмыслении окружающего мира и анализе информации.
Объем — это одно из фундаментальных понятий, которое помогает нам понять, что что-то принадлежит или не принадлежит определенной категории или классу. Он позволяет нам определить, насколько широко или узко мы говорим о каком-то предмете или явлении.
В данном тексте мы рассмотрим различные аспекты объема в логике, его применение в реальной жизни и важность его понимания для развития критического мышления. Будет интересно и познавательно, так что давайте начнем!
Определение понятия объем в логике
Знание объема важно для развития нашего мышления и логического мышления. Оно позволяет нам классифицировать и организовывать информацию, понимать отношения между понятиями и строить аргументы на основе логических законов.
Определение объема в логике имеет свои особенности в различных областях знания. Например, в математике объем может быть определен в терминах геометрических фигур и формул расчета их площади или объема. В философии объем может иметь более абстрактные определения и связан с концепциями сущности и смысла.
Определение объема также зависит от контекста. Например, в контексте компьютерных систем объем может относиться к объему хранения данных или емкости памяти, а в контексте лингвистики — к объему информации, содержащейся в тексте или речи.
Понимание понятия объем в логике помогает нам анализировать и объяснять мир вокруг нас. Оно позволяет нам разбираться в сложных системах, развивать наше мышление и применять логические принципы в нашей повседневной жизни. Используя свои навыки логического мышления и понимая объем, мы можем принимать более обоснованные и информированные решения в различных ситуациях.
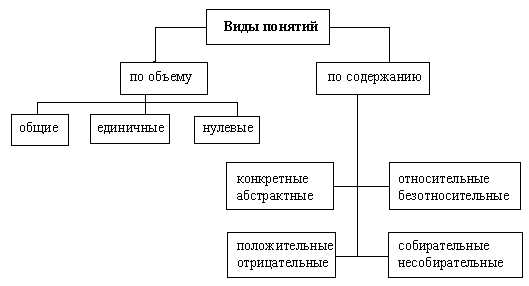
Виды объема в логике

В логике существует несколько видов объема, которые используются для разных целей и задач.
1. Кардинальный объем: Кардинальный объем, или числовой объем, относится к количеству элементов в множестве. Он может быть конечным или бесконечным. Например, если у нас есть множество всех целых чисел от 1 до 10, его кардинальный объем будет равен 10, так как в нем содержится 10 элементов. Если же рассматривать множество всех целых чисел, кардинальный объем будет бесконечным, так как в нем бесконечное количество элементов.
2. Функциональный объем: Функциональный объем относится к количеству возможных функций или отношений, которые можно определить на множестве. Например, если у нас есть множество из трех элементов, мы можем определить несколько различных функций на этом множестве, таких как функция, которая удваивает каждый элемент, и функция, которая возвращает сумму элементов. Таким образом, функциональный объем также является важной характеристикой при анализе множеств и их свойств.
3. Предметный объем: Предметный объем относится к количеству предикатов или высказываний, которые могут быть истинными или ложными в системе. Например, если у нас есть логическая система с двумя предикатами «A» и «B», предметный объем этой системы будет равен 2, так как у нас есть два предиката, которые можно истинными или ложными.
4. Модальный объем: Модальный объем относится к количеству возможных миров или состояний, которые могут существовать в системе. Он используется в исследованиях с множеством различных логических операторов, таких как возможность, необходимость и действительность. Модальный объем играет важную роль при анализе множеств и систем, где важно учитывать возможность различных состояний или миров.
Знание и понимание разных видов объема в логике помогает нам измерять и анализировать различные свойства и характеристики множеств и систем. Он дает нам возможность лучше понимать структуру и состав различных элементов в логических системах, что позволяет нам принимать более обоснованные и эффективные решения.
Применение объема в логике
Применение объема в логике очень широко. Оно используется для анализа и оценки различных принципов логического мышления, доказательств и рассуждений. Например, объем позволяет определить, является ли утверждение простым или сложным, ясным или нечетким, точным или неточным.
Кроме того, объем используется для анализа и оценки аргументов. Например, можно сравнить объем утверждений, которые поддерживают аргумент, с объемом утверждений, которые противоречат аргументу. Это позволит определить, насколько убедительным является данный аргумент.
Использование объема в логике позволяет более точно анализировать и оценивать утверждения и рассуждения, а также строить логически корректные аргументы. Он помогает развивать логическое мышление и способствует более глубокому и точному пониманию мира.
Объем в логике: понятие и применение
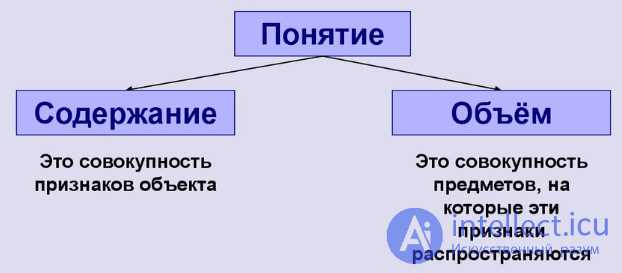
В логике объем применяется для анализа и определения структуры и свойств множеств, а также для классификации их по объему. Например, можно выделить множества конечного объема, бесконечного объема и счетного (перечислимого) объема.
Объем в логике является важным понятием, используемым при формулировании и изучении математических теорий, а также в различных областях науки, таких как информатика, физика, экономика и др. Знание объема множества позволяет анализировать их свойства, строить модели и проводить исследования, основанные на логических заключениях.