Когда мы обращаемся к математике, мы часто сталкиваемся с различными обозначениями, символами и формулами. Некоторые из них могут быть непонятными или запутанными для нас. Понимание обозначений в математике — важный навык, который поможет нам разобраться в сложных концепциях, решить задачу или просто улучшить наше математическое образование.
В этой статье мы рассмотрим, что означают обозначения в математике и как их использовать. Будем разбираться с обозначениями чисел, операций, переменных, функций и других основных понятий математики. Освоив эти основы, мы сможем гораздо лучше понимать и применять математические концепции в школе, университете или в повседневной жизни.
Значение обозначения в математике
Значение обозначения в математике заключается в том, что оно позволяет нам обмениваться информацией и коммуницировать на языке математики. Как и в любом другом языке, обозначения в математике имеют свои правила и соглашения, которые помогают нам понять и использовать эти обозначения.
Обозначения в математике могут быть символами, буквами, цифрами или специальными знаками. Например, символ «+» используется для обозначения сложения, а символ «×» — для обозначения умножения. Буквы могут представлять какие-либо переменные или константы, например, «x» может обозначать неизвестное число в уравнении.
Значение обозначения в математике заключается не только в его символическом значении, но и в его функциональности и контексте. Например, когда мы видим символ «√», мы понимаем, что это обозначение для извлечения квадратного корня. Однако, контекст может изменить значение обозначения. Если мы видим обозначение «√» перед отрицательным числом, то это может означать комплексное число.
Когда мы учимся и применяем математику, мы также учимся и использованию обозначений. При изучении нового математического понятия, мы узнаем его обозначение и понимаем его значение и смысл. С помощью обозначений мы можем записывать уравнения, доказывать теоремы и решать сложные проблемы.
Каждое обозначение в математике имеет свою историю и развитие. Оно может быть результатом работы и открытий многих математиков, которые стремились создать удобный и эффективный язык для описания математических концепций. Использование обозначений в математике позволяет нам общаться, сотрудничать и строить наработки других математиков, создавая таким образом целую общественность математиков, которая вносит вклад в развитие науки.
Таким образом, значение обозначения в математике не может быть недооценено. Оно помогает нам понимать и использовать язык математики, обмениваться информацией и сотрудничать в развитии этой удивительной науки.
Определение обозначения
В математике обозначение является важной частью коммуникации. Оно позволяет упростить и сократить запись и рассуждения, делая их более компактными и понятными. Без обозначений математические выражения были бы громоздкими и трудными для понимания.
Обозначение может включать различные элементы, такие как буквы, цифры, символы, операторы и функции. Например, в уравнении «x + 2 = 8», переменная «x» является обозначением неизвестного значения, а символ «+» обозначает операцию сложения.
Математические обозначения также могут использоваться для представления специфических свойств объектов или операций. Например, символ «π» используется для обозначения числа пи, а символ «√» обозначает операцию извлечения квадратного корня.
Обозначение в математике должно быть ясным и однозначным, чтобы избежать путаницы и неправильных интерпретаций. Правила и соглашения по использованию обозначений четко определены и установлены в математической нотации.
Хотите узнать больше о математическом обозначении? Ответьте на следующий вопрос:
Какие математические обозначения вы чаще всего используете в своих задачах и рассуждениях?
- Пиши их в комментариях ниже.
- Опиши, какую роль они играют в вашей работе и как они помогают вам проводить математические рассуждения.
- Если вы столкнулись с каким-либо трудностями или неуверенностью в использовании обозначений, поделитесь этим, и мы постараемся помочь.
Математическое обозначение является мощным и универсальным инструментом, который помогает нам понять и объяснить мир вокруг нас. Используйте его с уверенностью и креативностью!
Функции обозначения
Функции обозначения играют важную роль в математике, помогая нам ясно и точно описывать и обозначать различные математические концепции, операции и объекты. Они позволяют нам работать с абстрактными понятиями и оперировать числами, переменными, операторами и другими математическими элементами в удобной форме.
Одним из наиболее известных примеров функции обозначения является символ числа π (пи). Этот символ используется для обозначения отношения длины окружности к её диаметру. Благодаря этой функции обозначения мы можем легко записывать формулы, связанные с окружностями и другими кривыми, используя всего один символ.
Еще одной известной функцией обозначения является знак равенства (=). Этот символ используется для обозначения равенства двух математических выражений. Например, мы можем записать уравнение 2 + 3 = 5 и понять, что оба выражения (2 + 3 и 5) имеют одинаковое значение. Знак равенства является основой для работы с алгеброй и решения уравнений.
Еще одна функция обозначения, которой мы все пользуемся каждый день, это арифметические операторы, такие как плюс (+), минус (-), умножить (×) и делить (÷). Эти символы позволяют нам выполнять различные арифметические операции и считать числа.
Другие примеры функций обозначения могут включать знаки для возведения в степень (^), извлечения квадратного корня (√), а также символы для обозначения суммы (∑), произведения (Π) и дифференцирования (d/dx).
Функции обозначения не только упрощают запись математических выражений, но и улучшают их читаемость и понятность. Они помогают нам организовывать и структурировать наши вычисления, давая им логическую и систематическую форму. Благодаря функциям обозначения мы можем коммуницировать математические идеи и решения с другими людьми, независимо от языковых и культурных различий.
Понимание функций обозначения является важной частью математической грамотности и позволяет нам изучать и понимать сложные математические концепции и отношения. Умение использовать функции обозначения поможет нам развивать логическое мышление, абстрактное мышление и решать разнообразные математические задачи. Поэтому, будьте активны в исследовании и использовании функций обозначения и расширяйте свои математические навыки и знания!
Виды обозначений в математике
В математике обозначение играет важную роль. Оно позволяет нам записывать и передавать математические идеи, формулы, теоремы и решения. Существует множество различных обозначений, которые помогают нам описывать и понимать математические концепции.
Алфавитные обозначения
Алфавитные обозначения — это обозначения, которые используют буквы алфавита для представления различных математических величин и концепций. Например, переменные в математических выражениях обычно обозначаются буквами, такими как «x», «y» и «z». Также буквы могут использоваться для обозначения констант, параметров и других математических объектов.
Символы и знаки
Символы и знаки используются для обозначения различных математических операций, отношений и свойств. Например, знак «+» обозначает сложение, знак «=» обозначает равенство, символ «√» обозначает квадратный корень. Они позволяют нам записывать и читать математические выражения и уравнения.
Индексы и верхние/нижние индексы
Индексы и верхние/нижние индексы используются для обозначения различных переменных или коэффициентов, которые связаны с определенным объектом или формулой. Например, в математическом выражении «an» индекс «n» обозначает номер элемента последовательности «a». Верхние и нижние индексы также могут использоваться для обозначения степеней, координат и других свойств.
Математические символы
В математике используются различные математические символы, которые представляют определенные математические понятия. Некоторые популярные математические символы включают символ пи «π», символ бесконечности «∞», символ суммы «Σ» и символы для пределов, производных и интегралов.
Специальные обозначения
В математике также существуют специальные обозначения, которые используются для обозначения специфических математических концепций. Например, символы «∈» и «∉» обозначают принадлежность и непринадлежность элемента к множеству. Символы «∀» и «∃» используются для кванторов всеобщности и существования.
Все эти виды обозначений помогают нам записывать, передавать и понимать математические идеи и концепции. Они позволяют нам работать с математическими объектами и решать математические задачи. Понимание и использование этих обозначений является важным навыком для изучения и применения математики.
Символьные обозначения
Одним из основных способов обозначения в математике являются символьные обозначения. Когда вы видите символ, вы знаете, что он представляет определенную математическую идею или операцию. Символы помогают делать математику более компактной и понятной, а также позволяют математикам общаться между собой на языке символов.
В математике используется широкий спектр символов для обозначения различных математических объектов. Например, символ «х» может обозначать неизвестное число в алгебре, символ «π» обозначает число пи, а символ «∑» обозначает сумму.
Символы также могут использоваться для обозначения отношений между числами или величинами. Например, символ «≤» обозначает «меньше или равно», символ «≥» обозначает «больше или равно», а символ «=» обозначает «равно». Эти символы помогают нам сравнивать и устанавливать отношения между различными величинами.
Кроме того, символы могут использоваться для обозначения операций и функций. Например, символ «+» обозначает сложение, символ «×» обозначает умножение, а символ «√» обозначает извлечение квадратного корня. Эти символы предоставляют нам конкретные инструкции о том, как проводить вычисления.
Символьные обозначения играют важную роль в математике, помогая нам лучше понимать и использовать математические концепции. Они облегчают запись и чтение математических выражений, а также позволяют нам точнее и однозначно описывать математические идеи и операции.
Так что следующий раз, когда вы увидите символ в математической нотации, задайте себе вопрос: «Что этот символ обозначает и какую информацию он представляет?». Углубившись в изучение символов и их значений, вы сможете лучше понимать и применять математические концепции и операции.
Обозначение в математике: что оно значит и как использовать

Обозначения позволяют сократить запись математических выражений, делая их более компактными и удобными для чтения и анализа. Они являются основным инструментом коммуникации в математике и позволяют ученым и математикам обмениваться идеями и результатами исследований.
Некоторые обозначения особенно широко используются в математике:
- + и — – обозначают операции сложения и вычитания соответственно;
- * и / – обозначают операции умножения и деления соответственно;
- = – обозначает равенство;
- < и > – обозначают меньше и больше соответственно;
- ≤ и ≥ – обозначают меньше или равно и больше или равно соответственно;
- ( ) – обозначают округление или группировку выражений;
- { } – обозначают множества;
- [ ] – обозначают интервалы чисел.
Помимо этих обозначений, в математике используется множество других символов, включая греческие буквы, индексы, интегралы, производные и другие.
Важно использовать правильные обозначения и следовать правилам и соглашениям в математике, чтобы избежать путаницы и ошибок. Обозначения являются универсальными и используются во всех областях математики, включая алгебру, геометрию, анализ, статистику и другие.
| Обозначение | Значение |
|---|---|
| x | неизвестное значение или переменная |
| y | переменная или значение, зависящее от x |
| n | натуральное число |
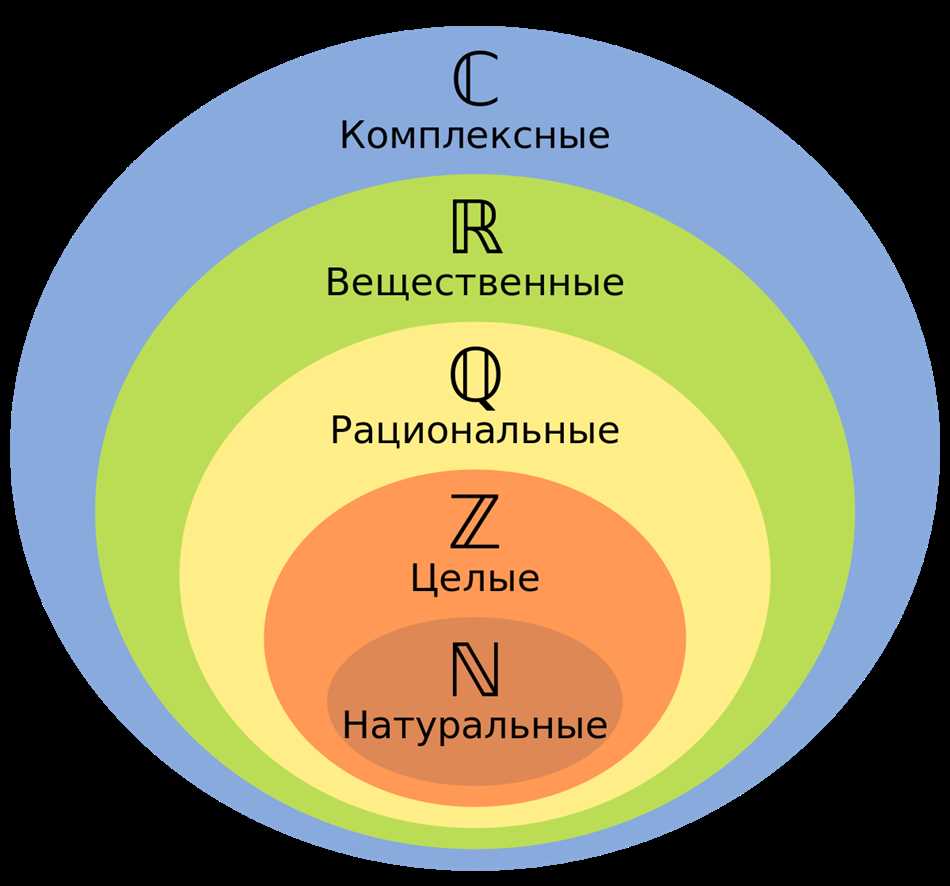
| ℝ | множество действительных чисел |
| ∑ | сумма |
| ∫ | определенный или неопределенный интеграл |
Знание и понимание обозначений в математике существенно облегчают работу с числами и формулами, а также помогают во взаимодействии и обсуждении результатов математических исследований.