Обратная функция: понятие и особенности

Здравствуйте! Сегодня поговорим о важном понятии в математике — обратной функции. Когда мы говорим о функциях, мы обычно думаем о том, какая «входная информация» дает нам «выходные данные». Но что, если мы хотим получить обратную информацию? Именно для этого и существует обратная функция.

Обратная функция — это функция, которая возвращает «входные данные», когда у нас уже есть «выходные данные». Например, если у нас есть функция, которая умножает число на 2, обратная функция будет делить число на 2.

Обратные функции обладают несколькими интересными свойствами. Одно из таких свойств — если мы применяем функцию к числу, а затем обратную функцию к полученному результату, мы получим обратно изначальное число.

Определение обратной функции

Другими словами, если у нас есть функция f(x), которая преобразует входное значение x в определенное выходное значение y, то обратная функция g(y) будет преобразовывать значение y обратно в его исходное значение x.

Пример:

Рассмотрим функцию f(x) = 2x.

Если мы возьмем число 4 и подставим его в функцию f(x), мы получим 8 (4 * 2 = 8).

Теперь, если мы возьмем число 8 и подставим его в обратную функцию g(y), мы должны получить исходное значение 4.

То есть, g(8) = 4.

Обратная функция нам помогает «отследить» исходные значения, которые были преобразованы функцией. Она позволяет нам восстановить исходные данные из результатов функции.

Обратная функция нередко используется в математике, физике, экономике и других областях, чтобы решать различные задачи и находить значения переменных, которые были преобразованы функцией.

Обратимость функций

Обратимость функций имеет важное значение в математике и во многих других областях знаний. Зачастую мы хотим найти обратную функцию для решения различных задач. Например, если мы имеем функцию, которая превращает температуру в градусах Цельсия в температуру в градусах Фаренгейта, мы можем найти обратную функцию, которая будет выполнять преобразование в обратном направлении.

Один из способов определить обратимость функции является проверка ее инъективности или сюръективности. Функция является инъективной, если каждому значению аргумента соответствует только одно значение функции. Например, функция y = 2x является инъективной, так как каждому значению x соответствует только одно значение y.

С другой стороны, функция является сюръективной, если для каждого значения функции существует значение аргумента, при котором функция равна этому значению. Например, функция y = x^2 является сюръективной, так как для каждого положительного значения y существует два значения x, при которых функция равна y.

Если функция является одновременно инъективной и сюръективной, то она называется биективной, и обратная функция всегда существует. Например, функция y = x является биективной, так как каждому значению x существует единственное значение y и наоборот.

Обратная функция обладает рядом свойств, которые делают ее полезной и важной в различных областях. Например, обратная функция сохраняет операции с функциями, такие как сложение, вычитание и композиция. Также обратная функция может использоваться для решения уравнений и поиска неизвестных значений.

Как найти обратную функцию?

Чтобы найти обратную функцию, нужно выполнить несколько шагов. Давайте посмотрим на примере функции:

Исходная функция: f(x) = 2x + 3

1. Вначале заменим саму функцию обратным обозначением: y = 2x + 3.

2. Затем переставим переменные местами: x = 2y + 3.

3. Постарайтесь получить y как отдельную переменную: x — 3 = 2y.

4. Выразим y: (x — 3)/2 = y.

5. Теперь тот факт, что у нас есть обратная функция f^-1(x), четко показывает, что:

f^-1(x) = (x — 3)/2.

Таким образом, мы нашли обратную функцию для f(x) = 2x + 3, которая является (x — 3)/2.

Важно отметить, что не все функции имеют обратные функции. Обратная функция существует только в том случае, если оно удовлетворяет условию, что для каждого значения y существует только одно значение x. Если исходная функция не является инъективной (или однозначной), то у нее нет обратной функции.

Когда вы находите обратную функцию, важно проверить ее, подставив значения исходной функции и убедившись, что они совпадают с их ожидаемыми значениями.

Теперь, когда вы знаете, как найти обратную функцию, вы можете использовать этот метод для решения уравнений и нахождения пропущенных значений переменных. Обратные функции являются мощным инструментом, который помогает нам лучше понять и использовать математические функции в нашей повседневной жизни.

Свойства обратной функции

Свойство 1: Отображение между множествами

Обратная функция является отображением между множествами исходной функции и множеством значений этой функции. Это означает, что для каждого значения в множестве значений исходной функции, существует одно и только одно значение в множестве исходной функции, которое соответствует обратной функции.

Свойство 2: Область определения и область значений

Область определения обратной функции равна области значений исходной функции, а область значений обратной функции равна области определения исходной функции. Это означает, что значения, которые можно использовать в исходной функции, также могут быть использованы в обратной функции.

Свойство 3: Симметричность

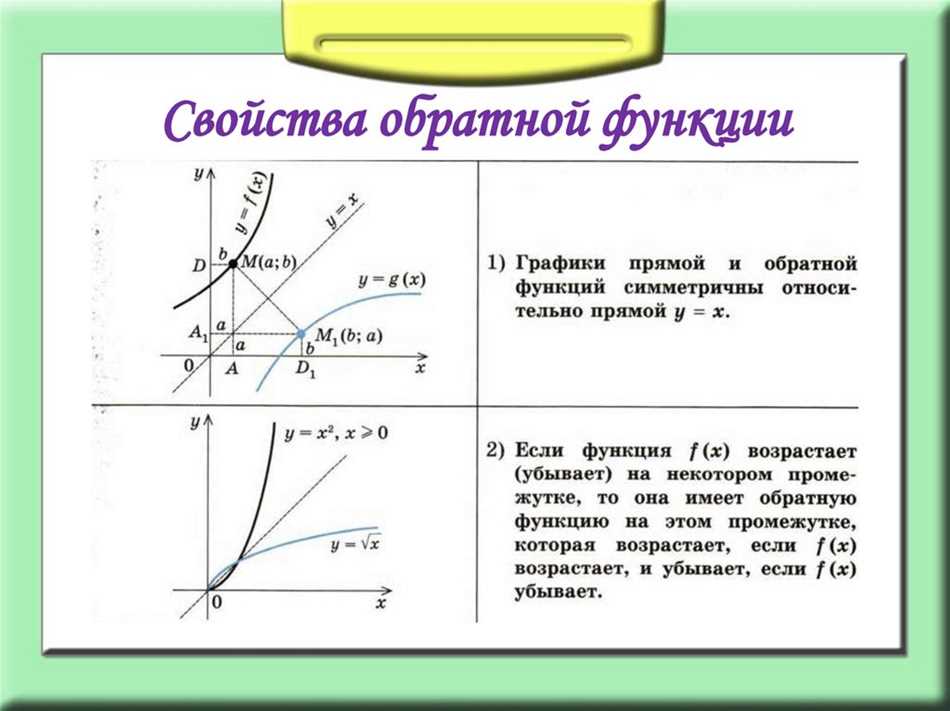
Обратная функция симметрична исходной функции относительно главной диагонали графика функции. Это означает, что если мы отображаем график исходной функции на декартовой плоскости, а затем получаем обратную функцию, мы получим точно такой же график, но отраженный относительно главной диагонали.

Свойство 4: Взаимо-обратные действия

Исходная функция и ее обратная функция выполняют взаимо-обратные действия. Это означает, что если мы применяем исходную функцию к значению, а затем применяем обратную функцию к результату, мы получим исходное значение. Аналогично, если мы применяем обратную функцию к значению, а затем применяем исходную функцию к результату, мы также получим исходное значение.

Знание свойств обратной функции поможет понять ее роль и использование в математике. Понимание обратных функций позволяет нам решать уравнения, обращать операции и анализировать зависимости между переменными. Это мощный инструмент, который помогает нам лучше понять мир вокруг нас и решать практические задачи.

График обратной функции

Чтобы понять, что такое график обратной функции, сначала вспомним, что такое обратная функция. Обратная функция f^-1(x) — это такая функция, которая обращает значение функции f(x) в его исходное значение x. Интуитивно можно представить это так: если f(x) переводит число x в число y, то обратная функция f^-1(y) будет переводить число y обратно в число x.

График обратной функции фактически является зеркальным отражением графика исходной функции относительно прямой y=x. Это означает, что координаты точек на графике обратной функции будут меняться местами с координатами точек на графике исходной функции.

Например, если точка (3, 5) лежит на графике исходной функции, то точка (5, 3) будет лежать на графике обратной функции. Это должно быть интуитивно понятно, так как исходная функция и обратная функция выполняют взаимное преобразование значений.

График обратной функции также обладает следующими свойствами:

• Точка на графике исходной функции будет соответствовать вертикальной прямой, пересекающей график обратной функции в точке, координаты которой равны значению функции на оси x.
• Функции, обладающие графиками, симметричными относительно прямой y=x, являются взаимно обратными.
• Если исходная функция имеет горизонтальные асимптоты на графике, то обратная функция будет иметь вертикальные асимптоты на своем графике и наоборот.

График обратной функции позволяет нам исследовать свойства и взаимоотношения между функциями. Он является важным инструментом для решения различных математических задач, а также для понимания основных понятий и свойств обратных функций.

Обратная функция: определение и свойства

Обратная функция обозначается как f^-1 и определяется следующим образом:

• Если f(x) = y, то f^-1(y) = x
• То есть, обратная функция описывает взаимное соответствие между значениями функции f(x) и их исходными аргументами x

Свойства обратной функции:

1. Обратная функция существует только тогда, когда исходная функция является биекцией
2. Если исходная функция является монотонно возрастающей или монотонно убывающей на своей области определения, то и обратная функция будет монотонной на своей области определения
3. Если исходная функция является строго монотонной на своей области определения, то и обратная функция будет строго монотонной на своей области определения
4. Если исходная функция имеет точки перегиба или точки разрыва на своей области определения, то обратная функция будет иметь точки перегиба или точки разрыва на своей области определения

Обратная функция эффективно используется при решении уравнений, поиске некоторых статистических параметров и других задачах.