Обратная функция в алгебре 10 класс: понятие и применение

Знание обратной функции в алгебре является важной частью курса для студентов 10 класса. Обратная функция представляет собой функцию, которая отображает значения, обратные исходной функции. То есть, если задана функция f(x), обратная функция f^(-1)(x) будет отображать значения, которые возвращаются обратно в f(x).

Понимание обратной функции играет ключевую роль в различных алгебраических и геометрических задачах, позволяя решать уравнения и находить значения переменных. Более того, оно имеет применение в различных сферах науки и технологий, таких как программирование, криптография и анализ данных.

Основные понятия

Разберемся с основными понятиями, связанными с обратной функцией в алгебре 10 класса: понятием и применением.

Обратная функция — это функция, обратная к заданной функции. Она выполняет обратное преобразование значений функции обратно в исходные значения.

Ключевым свойством обратной функции является то, что при композиции функции и ее обратной функции получается исходная функция. Другими словами, если f(x) — исходная функция, то ее обратная функция обозначается f^(-1)(x). И при выполнении условия f^(-1)(f(x)) = x, получается, что аргумент функции f(x) равен x.

Рассмотрим пример. Пусть у нас есть функция f(x) = 2x. Чтобы получить обратную функцию, нам нужно найти такую функцию, которая обратно преобразует результаты функции f(x) в исходные значения.

Чтобы найти обратную функцию, мы можем применить несколько методов. Один из них — использование обратной операции, которая выполняет обратное преобразование. В данном случае, чтобы найти обратную функцию, мы можем использовать деление на 2, так как это обратная операция для умножения на 2. Таким образом, обратная функция f^(-1)(x) будет равна f(x)/2.

Теперь мы можем проверить, является ли f^(-1)(x) действительно обратной функцией для f(x). Для этого мы должны убедиться, что f^(-1)(f(x)) = x. В нашем случае, f^(-1)(f(x)) = (2x)/2 = x, что подтверждает, что f^(-1)(x) — обратная функция для f(x).

Обратные функции имеют важные применения в математике и других областях. Они могут использоваться для решения уравнений, определения области значений и области определения исходной функции. Также они играют ключевую роль в обратной задаче, которая заключается в нахождении значений исходной функции, зная значения ее обратной функции.

Итак, основные понятия обратной функции в алгебре заключаются в том, что обратная функция — это функция, обратная к заданной функции, и обладает свойством композиции с исходной функцией, которая равна аргументу функции. Обратные функции широко применяются для нахождения решений уравнений и определения областей значений и областей определения функций.

Обратная функция

Чтобы понять, что такое обратная функция, давайте рассмотрим пример. Предположим, у нас есть функция f(x), которая умножает число на 3. То есть, если мы подставим число 2 в эту функцию, мы получим результат 6 (2 * 3 = 6). Обратная функция этой функции будет делить число на 3. То есть, если мы подставим число 6 в обратную функцию, мы получим результат 2 (6 / 3 = 2).

Обратная функция обычно обозначается как f^-1(x), где f(x) — исходная функция. Имейте в виду, что обратная функция может не всегда существовать. Например, если у нас есть функция f(x) = x², то ее обратная функция будет неоднозначной (т.е. у нее будет несколько значений для одного исходного значения). Это происходит из-за того, что возведение в квадрат убирает отрицательный знак, и поэтому не существует единственного обратного значения для каждого исходного значения.

Обратные функции могут быть полезными при решении уравнений. Например, если у нас есть уравнение f(x) = 4x — 7, мы можем использовать обратную функцию, чтобы решить его и найти значение x. Для этого мы просто подставляем значение y в обратную функцию f^-1(y), и находим значение x.

Использование обратных функций может быть очень полезным в решении различных математических проблем. Они позволяют нам переходить между исходными значениями и значениями, полученными от функции, что делает их мощным инструментом для алгебры и математики в целом. Поэтому, изучение и понимание обратных функций является ключевым элементом в освоении алгебры и в решении математических задач.

Область определения

Представь, что у тебя есть функция, которая преобразует числа. Но не все числа подходят для этой функции. Например, если у нас есть функция «деление на x», то для нее нельзя использовать значение x=0, потому что на ноль делить нельзя. В этом случае областью определения будет все множество действительных чисел, за исключением нуля.

Чтобы найти область определения функции, нужно внимательно проанализировать все ограничения, которые могут появиться при решении задачи. Нужно учитывать такие факторы, как деление на ноль, извлечение корня из отрицательного числа и т.д.

Например, рассмотрим функцию «квадратный корень из x». В этом случае область определения будет все множество неотрицательных действительных чисел, так как из отрицательных чисел нельзя извлечь квадратный корень.

Понимание области определения функции поможет нам установить допустимые значения для аргументов и избежать ошибок в решении задач. Это очень важно, чтобы функция имела смысл и была определена на всех нужных нам значениях.

Вот и всё, что я хотел рассказать о понятии «область определения». Надеюсь, теперь тебе понятно, что это такое и как найти область определения функции. Удачи в изучении алгебры!

Поиск обратной функции

Шаг 1: Определение функции

Прежде чем мы начнем искать обратную функцию, нам нужно определить, какая функция у нас есть. Функция — это отображение множества элементов из одного множества в другое. Она может быть задана уравнением, графиком или словесным описанием. Например, пусть у нас есть функция f(x) = 2x + 3.

Шаг 2: Замена переменных

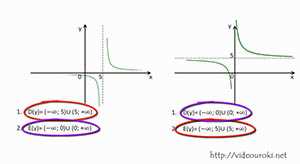
Чтобы найти обратную функцию, мы должны заменить переменные. Наша основная функция имеет переменную x, поэтому мы заменим x на y и y на x. Таким образом, наша функция станет f(y) = 2y + 3.

Шаг 3: Решение уравнения

Теперь мы должны решить уравнение f(y) = x относительно y. Прежде всего, мы выразим y через x. Для нашей функции f(y) = 2y + 3 это будет выглядеть так: y = (x — 3) / 2.

Шаг 4: Запись обратной функции

Теперь, когда мы нашли значение y в зависимости от x, мы можем записать обратную функцию. Для нашего примера обратной функцией будет f^-1(x) = (x — 3) / 2.

Вот и все! Мы нашли обратную функцию для исходной функции f(x) = 2x + 3.

Обратите внимание, что не все функции имеют обратные функции. Обратная функция существует только тогда, когда функция является взаимно однозначным отображением. Это означает, что каждому элементу входного множества соответствует только один элемент выходного множества. Если функция не является взаимно однозначной, ее обратная функция не существует.

Поиск обратной функции может быть сложным процессом, но он имеет множество практических применений. Например, обратные функции могут использоваться в криптографии для шифрования и дешифрования информации. Они также могут быть полезны в физике, экономике и других областях науки.

Важно понимать, что обратная функция является мощным инструментом, который может помочь нам понять и анализировать сложные математические модели. Надеюсь, этот материал был полезен для вас, и вы теперь лучше понимаете, как искать обратную функцию. Удачи в ваших математических исследованиях!

Процесс нахождения обратной функции

Для того чтобы найти обратную функцию, необходимо выполнить ряд шагов.

Шаг 1: Определение существования обратной функции

Первым делом необходимо узнать, существует ли обратная функция в данном случае. Для этого нужно проверить нашу исходную функцию на инъективность, то есть на то, что она не принимает одно и то же значение для разных аргументов. Если функция является инъективной, то она имеет обратную функцию.

Шаг 2: Нахождение формулы для обратной функции

Далее необходимо найти формулу для обратной функции. Для этого мы должны заменить переменные в исходной функции так, чтобы зависимость между аргументом и значением функции поменялась местами. То есть, если в исходной функции аргументом является переменная x, а результат функции обозначается как f(x), в обратной функции аргументом будет f(x), а результатом будет x.

Процесс нахождения такой формулы может быть сложным и требовать применения различных методов, в зависимости от сложности исходной функции. Иногда может потребоваться использование теорем и математических операций.

Шаг 3: Проверка обратной функции

После нахождения формулы для обратной функции, третий шаг состоит в проверке правильности нашего решения. Для этого мы можем подставить значения в оба выражения и убедиться, что получаем одинаковый результат. Это поможет нам убедиться в том, что наша обратная функция работает корректно.

Процесс нахождения обратной функции может быть сложным и требует от нас внимательности и тщательности. Однако, умение находить обратную функцию может быть очень полезным в многих ситуациях, особенно в математических и физических задачах. Научиться находить обратную функцию поможет нам лучше понимать зависимости между различными переменными и решать сложные задачи.

Обратная функция в алгебре 10 класс: понятие и применение

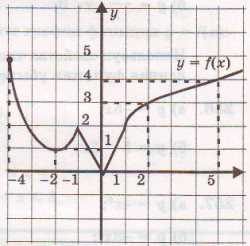
Для того чтобы функция имела обратную функцию, она должна быть взаимно-однозначной. Это означает, что каждому x должен соответствовать единственный y (f(x)), и наоборот, каждому y должен соответствовать единственный x (f^-1(y)).

Применение обратных функций в алгебре и математике в целом очень широко. Они позволяют решать уравнения, находить значения переменных, находить обратные преобразования и многое другое.

Зная обратную функцию, мы можем решать уравнения вида f(x) = y. Для этого нужно применить обратную функцию к обеим частям уравнения: f^-1(f(x)) = f^-1(y), получив x = f^-1(y).

Обратные функции также помогают находить значения переменных, связанных с основной функцией. Например, если у нас есть функция f(x) = 2x, то обратная функция будет f^-1(x) = x/2. Это значит, что если мы знаем значение x, мы можем легко найти соответствующее значение f(x) и наоборот.

Кроме того, обратные функции используются для нахождения обратных преобразований. Например, если у нас есть функция, которая увеличивает число на 2, мы можем использовать обратную функцию, чтобы вернуть число обратно. В данном случае обратная функция будет уменьшать число на 2.