Одночлены в 7 классе: основные понятия и методы их поиска

В седьмом классе математики начинают изучать одночлены. Но что это такое и зачем они нужны? Одночлен — это алгебраическое выражение, состоящее из одной переменной и ее степени, умноженой на коэффициент. Хотите научиться искать одночлены? Вам понадобится разобраться с понятием переменной, коэффициента и степени. Затем, вы сможете определить, является ли алгебраическое выражение одночленом. Не волнуйтесь, это не так сложно, как может показаться на первый взгляд. В этой статье мы рассмотрим несколько примеров и дадим вам полезные советы по поиску одночленов.

Что такое одночлены?

Одночлены — это математические выражения, которые состоят из одного члена. То есть, это выражения, где нет никаких математических знаков, кроме умножения или деления. Такие выражения могут содержать только числа, переменные или их произведения.

Давай рассмотрим несколько примеров, чтобы прояснить, о чем я говорю. Если у нас есть выражение вида 3x, то это и есть одночлен. Здесь у нас есть число 3 и переменная x, которые умножаются между собой. Вот еще один пример: 2y^2. В этом выражении у нас есть число 2 и переменная y, которая возводится во вторую степень.

Теперь, когда мы знаем, что такое одночлены, давай попробуем их найти в некоторых выражениях. Представь, что у тебя есть выражение 4x + 5y. Но нам нужно найти только одночлены, поэтому мы можем выделить два одночлена здесь: 4x и 5y. Обрати внимание, что эти выражения содержат только произведение чисел и переменных.

Теперь попробуй самостоятельно найти одночлены в следующих выражениях: 2a + 3b, 6xy + 4z, 7m^2 + 9n^3. Подумай, что здесь может быть одночленом, а что нет, и почему.

Важно помнить, что одночлены — это основа алгебры, и они часто используются для упрощения и работы с более сложными выражениями. Знание одночленов поможет тебе лучше понимать алгебру и справляться с математическими задачами более эффективно.

Надеюсь, теперь ты лучше понимаешь, что такое одночлены и как их искать. Математика может быть интересной и поэтому не стоит бояться мысленно «играть» с числами и переменными. Удачи в твоих математических исследованиях!

Как искать одночлены?

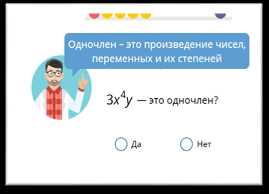
Одночлен – это выражение, которое состоит из одного члена. Вот пример одночленов: 3x, -2y, 5a^2. Если ты обратишь внимание, то у каждого одночлена есть коэффициент (число перед переменной) и переменная или переменные с целочисленными показателями (степени).

Итак, как найти одночлен в алгебраическом выражении? Пожалуйста, обрати внимание на следующие указания:

1. Идентифицируй члены с переменными. Они обычно состоят из букв (или буквы) и возможно имеют степенные показатели (натуральные числа, которые указывают на сколько раз нужно умножить переменную).
2. Идентифицируй коэффициенты. Они обычно являются числами, стоящими перед переменными. Если числа нет, это означает, что коэффициент равен 1.
3. Учти знаки. Одночлен может быть положительным (+) или отрицательным (-). Знак стоит перед выражением.

Теперь давай рассмотрим примеры, чтобы все стало яснее.

• В выражении 4x^2 + 2xy — 3z, у нас есть три одночлена: 4x^2, 2xy и -3z.
• В выражении -5a — 7b^2 + c, имеется три одночлена: -5a, -7b^2 и c. Обрати внимание, что перед c нет видимого коэффициента, поэтому его можно считать равным 1.

Продолжай тренироваться с примерами и скоро научишься мгновенно идентифицировать одночлены в алгебраических выражениях. Воспользуйся этими шагами, проверяй себя и задавай себе вопросы, чтобы увидеть, где находятся одночлены и с чем они связаны.

Успервай искать одночлены в уравнениях и алгебраических выражениях. Это важнейший навык, который пригодится тебе не только в математике, но и в реальной жизни. Это связано с рассуждениями, анализом и логикой. Итак, с нетерпением жду, когда ты станешь настоящим экспертом в нахождении одночленов!

Примеры задач на одночлены

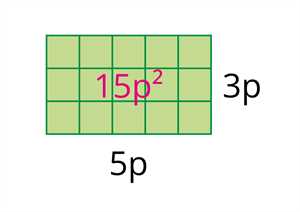
Давайте рассмотрим несколько примеров задач на одночлены, чтобы увидеть, как они применяются на практике:

1. Задача 1: Умножьте одночлены 3x и 4y.

   Решение: Применяем правило умножения одночленов — перемножаем числовые коэффициенты (3 и 4) и перемножаем переменные (x и y): 3x * 4y = 12xy.

2. Задача 2: Разделите одночлен 10a² на 2a.

   Решение: Применяем правило деления одночленов — делим числовые коэффициенты (10 и 2) и делим переменные (a² и a): 10a² / 2a = 5a^2-1 = 5a.

3. Задача 3: Выразите одночлен 2ab — ac в виде общего множителя и остатка.

   Решение: Одинаковое слагаемое в каждом члене — это a. Одночлен можно представить в виде a(2b — c).

4. Задача 4: Представьте сумму одночленов 3x, 4y и 2z в виде одного выражения.

   Решение: Все члены имеют разные переменные, поэтому их нельзя объединить в один одночлен. Сумму можно представить как 3x + 4y + 2z.

В этих примерах мы видим, как одночлены используются для упрощения и выражения выражений в алгебре. Они помогают нам сократить сложные выражения до более простых и удобных для работы.

Задачи на одночлены также могут быть более сложными и требовать применения различных правил и свойств. Они могут включать в себя более одной переменной и использование операций сложения, умножения и деления одночленов.

Надеюсь, эти примеры задач помогли вам лучше понять, как работать с одночленами и как применять их в различных ситуациях. Не стесняйтесь практиковаться и решать больше задач, чтобы улучшить свои навыки в алгебре!

Одночлены в 7 классе: что это такое и как их искать?

Для нахождения одночленов в выражении нужно следовать нескольким правилам:

• Одночленом может быть выражение только с одним членом. Например, 5x, -3y, 2xy.
• Члены в одночлене могут быть только сложены или вычтены друг из друга. Например, 2x + 3y — 5z.
• Коэффициенты и переменные в одночленах могут быть умножены только друг на друга. Например, 4xy, -2yz, 7a^2.
• Степени переменных в одночленах должны быть натуральными числами. Например, 3x^2, 2a^3b^4, 5xy.

Для нахождения одночленов в выражении нужно исключить все арифметические операции, которые не позволяют получить одночлен и посмотреть на части выражения отдельно. После этого нужно определить, является ли каждая часть выражения одночленом или нет, и если да, то записать его.

1. Пример: 4x + 3y — 5z.
2. Исключаем сложение и вычитание: 4x, 3y, -5z.
3. Каждая часть является одночленом.
4. Записываем одночлены: 4x, 3y, -5z.

Таким образом, одночлены в выражении 4x + 3y — 5z являются 4x, 3y и -5z.