Когда речь идет об односвязных областях, возможно, многие из нас испытывают сложности с пониманием этого понятия. Но не беспокойтесь, я здесь, чтобы помочь разобраться!
Односвязная область — это концепция, которая используется в математике и физике для описания области пространства, которая полностью связна или не разрывается на части.
Односвязные области имеют некоторые уникальные характеристики, такие как отсутствие отверстий или «дыр», а также возможность перехода между любыми двумя точками внутри области без пересечения границы.
Понимание и использование односвязных областей имеет широкие применения в различных областях, включая геометрию, топологию и физику, и может быть полезным инструментом для анализа и понимания различных процессов и явлений.
Что такое односвязная область?
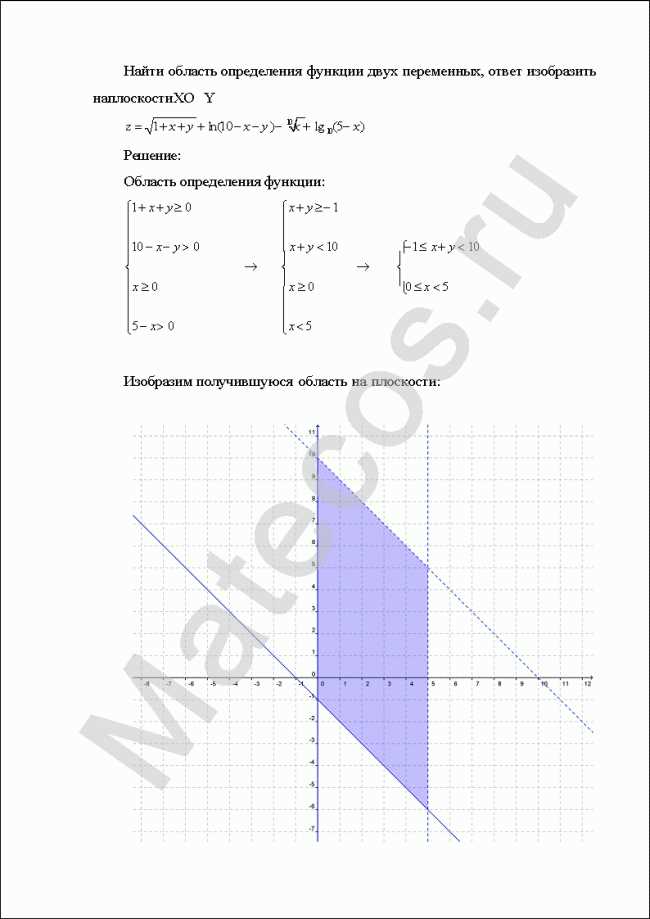
Для начала, односвязная область — это область, в которой любые две точки могут быть соединены непрерывным путем без пересечения границы этой области. Другими словами, если вы возьмете любые две точки в односвязной области и будите двигаться постепенно от одной точки к другой, то вам не придется касаться или пересекать границу области.
Например, представьте себе изображение глаза на бумаге. Внутри границы этого изображения можно провести непрерывный путь от любой точки к любой другой точке, не выходя за пределы области. Вот это и есть односвязная область.
Односвязные области имеют множество интересных свойств и применений. Изучение их может помочь понять основы топологии и проводить анализ сложных математических моделей. Например, односвязные области играют важную роль в решении дифференциальных уравнений и в изучении гармонических функций.
Кроме того, односвязные области имеют практическое применение в различных областях, таких как картография, робототехника и компьютерная графика. Они позволяют удобно определить границы объектов и позволяют проектировать эффективные алгоритмы для работы с геометрическими данными.
Характеристики односвязной области

Одна из основных характеристик односвязной области – это то, что она представляет собой связное, непрерывное пространство, где любые две точки можно соединить непрерывным путем. Это значит, что от одной точки до другой всегда можно добраться без пересечения границы области. Такая связность позволяет проводить различные математические операции внутри односвязной области и исследовать ее свойства.
Односвязная область имеет еще одну важную характеристику – она не содержит пустот или отверстий. Это означает, что внутри области нет препятствий или областей, которые не связаны с внешней границей. Это свойство делает односвязную область компактной и цельной, позволяя проводить анализ и решать уравнения внутри нее с меньшими трудностями.
Кроме того, односвязная область является гладкой и безразрывной. Это значит, что ее граница не имеет острых углов, пиков или вогнутостей. Гладкость границы облегчает проведение математических операций и упрощает работу с уравнениями, поскольку исключается возможность наличия особых точек или разрывов, которые могут создать сложности в анализе и решении задач.
Все эти характеристики делают односвязную область привлекательной для изучения и использования в математике. Односвязные области широко применяются в различных областях, таких как физика, инженерия и компьютерная графика, и позволяют проводить более точные и точные аналитические расчеты.
- Связность: обеспечивает непрерывное перемещение от одной точки к другой внутри области.
- Отсутствие пустот: область не содержит препятствий или отверстий, что обеспечивает ее компактность.
- Гладкость: граница области не имеет острых углов или разрывов, делая ее безразрывной.
Таким образом, односвязная область – это уникальное пространство с определенными условиями, которые делают ее особенной и интересной для анализа и исследования. Изучение односвязных областей позволяет математикам и ученым лучше понять пространственные свойства, развивать новые методы и решать сложные задачи в различных областях науки и техники.
Односвязная область: определение и характеристики
Характеристики односвязной области:
- У односвязной области есть одна граница, которая представляет собой замкнутый контур.
- Односвязная область не пересекается сама с собой, то есть не содержит отверстий или «дыр».
- Для прохождения от одной точки до другой в односвязной области достаточно пройти по всей границе, без необходимости пересечения внутренней части области.
- Односвязная область является простой областью, то есть не содержит самопересечений границы.
Примером односвязной области может служить любой контур на плоскости, не имеющий отверстий или самопересечений. Такие области широко используются в различных областях науки и техники, включая математику, физику, графический дизайн и компьютерную графику.