Окружность — это геометрическая фигура, состоящая из всех точек на плоскости, которые находятся на одинаковом расстоянии от фиксированной точки, называемой центром окружности. Эта фигура имеет множество свойств, которые делают ее уникальной и привлекательной для изучения.
Самое замечательное свойство окружности — ее равенство длины всех дуг. Независимо от размера окружности, каждая дуга будет иметь одинаковую длину согласно своему углу.
Еще одно важное свойство окружности — ее способность к вращению. Окружность может вращаться вокруг своего центра, оставаясь неизменной формы и размера.
Исследование окружности позволяет нам лучше понять ее свойства и использовать их в различных областях науки и техники. Теперь давайте рассмотрим более подробно некоторые из этих свойств.
Что такое окружность?
Окружность — это фигура, которая состоит из всех точек, находящихся на одинаковом расстоянии от заданной точки, называемой центром окружности. Расстояние от центра до любой точки окружности называется радиусом. Соответственно, радиус — это отрезок, соединяющий центр окружности с любой точкой на ее границе.
А теперь представь, что ты находишься в центре окружности. Куда бы ты ни посмотрел, все точки, которые ты увидишь, будут находиться на одинаковом расстоянии от тебя. И это расстояние будет одинаковым для любой точки на окружности. Звучит удивительно, не правда ли? Но именно так и работает окружность!
Окружности встречаются повсюду в нашей жизни. Например, в колесах автомобилей или в шинах велосипеда, в пиццах, на которых отмечены разрезы для разделения на равные части, и даже в наших глазах! Да, зрачки наших глаз имеют форму окружности и позволяют нам видеть все вокруг с одинаковой ясностью.
Окружности также имеют множество интересных свойств и формул, которые позволяют изучать их глубже и применять в различных областях, таких как геометрия, физика, инженерия и даже в программировании.
Теперь, когда ты знаешь, что такое окружность, попробуй задачку. Сможешь ли ты найти радиус окружности, если тебе дана ее длина? Подумай немного и найди решение в своей голове. Готов? Тогда проверь свой ответ вместе с нами!
Уравнение окружности
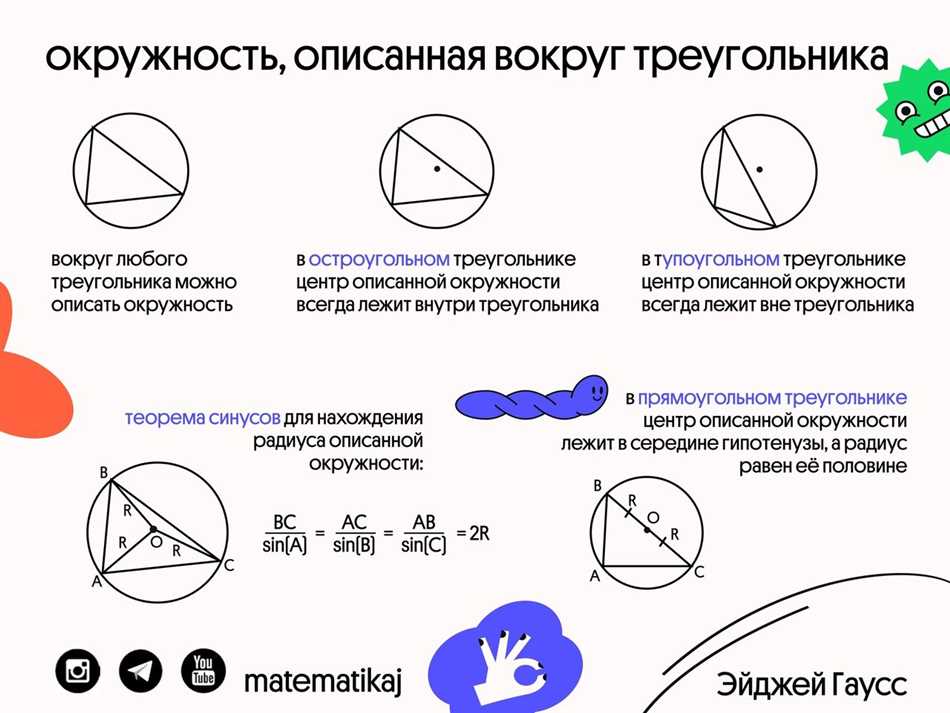
Представлять окружность в виде графического изображения или выразить ее уравнением не всегда просто, но с некоторыми простыми правилами это можно сделать. Основная идея заключается в использовании формулы длины окружности и формулы площади окружности.
Уравнение окружности в пространстве
Пусть (x,y) — координаты точки на плоскости, R — радиус окружности, (a, b) — координаты центра окружности. Уравнение окружности имеет следующий вид:
(x - a)² + (y - b)² = R²
Примеры уравнений окружности
Давайте рассмотрим несколько примеров, чтобы лучше разобраться в уравнении окружности:
- Уравнение окружности с центром в точке (0,0) и радиусом 3 будет иметь вид:
x² + y² = 9 - Уравнение окружности с центром в точке (2,4) и радиусом 5 будет иметь вид:
(x - 2)² + (y - 4)² = 25
Уравнение окружности позволяет нам легко определить все точки, которые лежат на окружности. Для этого достаточно задать центр окружности и радиус. Подставляя значения координат и радиуса в уравнение, мы можем получить координаты всех точек на данной окружности.
Уравнение окружности имеет большое практическое применение в различных областях науки и техники. Изучая уравнение окружности, мы можем решать задачи связанные с построением окружностей, определением расстояний, а также моделированием и анализом различных систем.
Таким образом, уравнение окружности является важным инструментом геометрии, который помогает нам лучше понять и использовать данную геометрическую фигуру. При изучении уравнения окружности мы расширяем свои знания и познаем новые аспекты математики.
Радиус и диаметр окружности
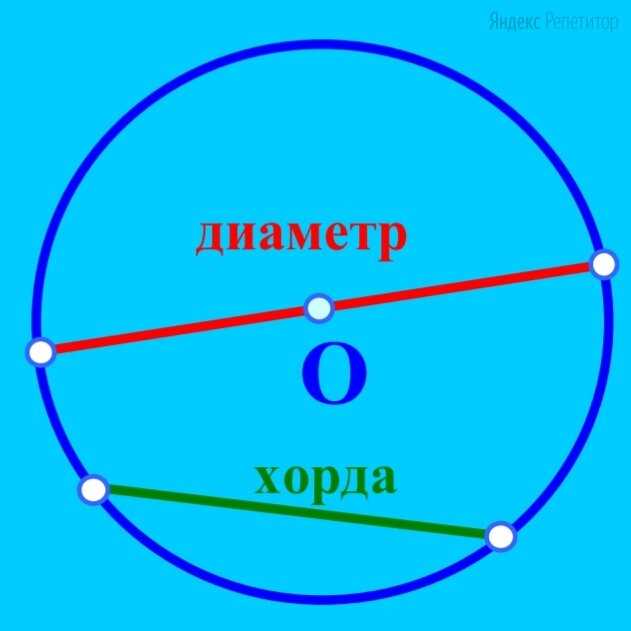
Радиус окружности — это расстояние от центра окружности до любой ее точки. Радиус обозначается буквой «r». Он всегда одинаков для всех точек окружности, так как они находятся на одном и том же расстоянии от центра. Радиус является половиной диаметра окружности.
Диаметр окружности — это отрезок, соединяющий две точки на окружности и проходящий через ее центр. Диаметр также является длиной отрезка, соединяющего любые две точки на окружности, проходящие через ее центр. Диаметр обозначается буквой «d». Диаметр окружности всегда равен двум радиусам.
Между радиусом и диаметром окружности существует простая математическая связь: диаметр равен удвоенному радиусу, а радиус равен половине диаметра. Если мы знаем длину диаметра окружности, мы можем легко найти длину радиуса и наоборот.
Зная радиус или диаметр окружности, мы можем вычислить различные характеристики окружности, такие как ее площадь и длина окружности. Диаметр является важным параметром при рассмотрении свойств окружности, так как многие формулы и соотношения используют его.
Важно помнить, что радиус и диаметр окружности тесно связаны и играют ключевую роль в геометрии окружности. Понимание этих терминов поможет вам лучше понять свойства и отношения в этой интересной и важной геометрической фигуре.
Дуги и хорды окружности
Дуги окружности
Дуга окружности – это часть окружности, ограниченная двумя точками. Обычно дуга обозначается двумя точками, например, через AB. Дуги могут быть разных размеров – как маленькими, так и большими, включая полную окружность.
Дуги окружности имеют много интересных свойств и могут применяться в различных задачах. Например, дуги участвуют в измерении углов и расстояний на окружности. Кроме того, они также часто используются при решении задач по геометрии и тригонометрии.
Хорды окружности
Хорда окружности – это отрезок, начало и конец которого находятся на окружности. Обычно хорда обозначается двумя точками, например, через AB. Хорды являются основой для изучения других элементов окружности, таких как радиус, диаметр и тангента.
Хорды окружности также обладают своими свойствами. Например, хорда может быть прямой или криволинейной, а длина хорды зависит от ее удаленности от центра окружности.
Важное замечание

Дуги и хорды являются важными элементами окружности и играют важную роль в различных математических задачах. Изучение этих элементов не только поможет вам лучше понять геометрию окружности, но и разовьет ваши навыки решения математических задач.
Задайте себе вопрос: Какую роль играют дуги и хорды в геометрии окружности? Каких результатов можно достичь, изучая эти элементы окружности? Используйте свои знания и навыки, чтобы решить математические задачи, связанные с дугами и хордами окружности. Помните, что геометрия – это не только теория, но и практическое применение в реальной жизни.
Окружность: определение и свойства
Окружность имеет следующие свойства:
- Длина окружности: Длина окружности равна произведению радиуса на двойное число π (пи). Обозначается как L = 2πr, где L — длина окружности, r — радиус окружности.
- Площадь круга: Площадь круга равна произведению квадрата радиуса на число π (пи). Обозначается как S = πr^2, где S — площадь круга, r — радиус окружности.
- Теорема Пифагора для окружности: Если две хорды пересекаются внутри окружности, то произведение отрезков каждой хорды, являющихся ее сегментами, равно.
- Теорема Талеса для окружности: Если две хорды пересекаются вне окружности, то произведение отрезков каждой хорды, являющихся ее сегментами, равно.
- Определение окружности в терминах уравнения: Уравнение окружности в декартовой системе координат имеет вид (x — a)^2 + (y — b)^2 = r^2, где (a, b) — координаты центра окружности, r — радиус окружности.
Окружность является основной элементом геометрии и находит применение в различных научных и практических областях, таких как физика, астрономия, инженерия и многие другие.