Оператор дифференцирования: основы и применение

Когда мы говорим о функциях и их изменении, оператор дифференцирования играет ключевую роль. Он позволяет нам изучать, как функция меняется в зависимости от изменения ее аргумента. Оператор дифференцирования вычисляет производную функции и помогает нам понять ее скорость изменения. Он используется в таких разных областях, как физика, экономика, инженерия и многое другое. Без него мы бы не смогли анализировать сложные зависимости и предсказывать будущие значения функций. В этой статье мы разберемся, что такое оператор дифференцирования и как его применять в практических задачах.

Определение оператора дифференцирования

Оператор дифференцирования записывается обычно как d/dx, где d означает дифференциал, а dx — переменную, по которой производится дифференцирование. Оператор дифференцирования может быть применен к любой функции, определенной на интервале числовой прямой.

Дифференцирование — это процесс нахождения производной функции. Производная функции в данной точке является угловым коэффициентом касательной к графику функции в этой точке. Дифференцирование позволяет определить, как функция меняется в каждой точке ее области определения, и находить экстремумы функций, точки перегиба, а также решать множество дифференциальных уравнений.

Оператор дифференцирования может использоваться в различных областях науки и техники. Например, в физике он применяется для описания скорости и ускорения тела, а в экономике — для изучения темпов роста и изменений.

С использованием оператора дифференцирования можно решать множество задач и находить точные значения производных для различных функций. Он является сильным инструментом в математике и имеет широкое применение в других научных дисциплинах. Познакомившись с основами оператора дифференциирования, вы сможете лучше понять мир вокруг вас и использовать его в своих исследованиях и решении задач.

Математические свойства оператора дифференцирования

• Линейность: Оператор дифференцирования обладает свойством линейности, что означает, что при дифференцировании линейной комбинации функций, можно сначала дифференцировать каждую функцию по отдельности, а затем сложить результаты. Например, если у нас есть функции f(x) и g(x), и константы a и b, то производные линейной комбинации af(x) + bg(x) равны a*f'(x) + b*g'(x). Это свойство очень удобно при дифференцировании сложных функций.
• Производная сложной функции: Оператор дифференцирования позволяет находить производную сложной функции. Для этого применяется цепное правило дифференцирования, которое гласит, что производная сложной функции равна произведению производной внешней функции на производную внутренней функции. Например, если у нас есть функция f(g(x)), то ее производная равна f'(g(x))*g'(x).
• Дифференцирование степенной функции: Оператор дифференцирования позволяет находить производную степенной функции. Для этого используется формула дифференцирования степенной функции, которая гласит, что производная функции f(x) = x^n равна n*x^(n-1), где n — степень функции. Это свойство позволяет находить производные множества различных функций.
• Производная суммы и разности функций: Оператор дифференцирования позволяет находить производную суммы и разности функций. Для этого достаточно просто взять производную каждой функции по отдельности и сложить или вычесть результаты. Например, если у нас есть функции f(x) и g(x), то производная суммы f(x) + g(x) равна f'(x) + g'(x), а производная разности f(x) — g(x) равна f'(x) — g'(x).

Эти свойства оператора дифференцирования позволяют упростить и ускорить процесс нахождения производных функций. Они являются основой для решения различных задач в физике, экономике, инженерии и других областях науки.

Применение оператора дифференцирования в физике

Одним из основных применений оператора дифференцирования в физике является определение скорости и ускорения объектов. Дифференцирование позволяет нам вычислить скорость как производную по времени от перемещения, а ускорение — как производную скорости по времени. Эти величины играют ключевую роль в механике и движении тел.

Оператор дифференцирования также используется для описания изменений физических величин в пространстве. Например, векторное дифференцирование используется в электромагнетизме для описания распределения электрического и магнитного поля в пространстве. Производные по координатам и времени позволяют нам понять, как поля меняются от точки к точке и со временем.

Оператор дифференцирования также широко применяется в термодинамике и статистической физике для анализа тепловых процессов и изменения энергии системы. Дифференциальные уравнения, содержащие производные по времени и пространственным координатам, позволяют нам решать различные задачи, связанные с теплопередачей, теплообменом и равновесием систем.

Оператор дифференцирования также находит применение в квантовой физике, где дифференцирование по времени позволяет нам описывать динамику квантовых систем и эволюцию их состояний. Операторы дифференцирования применяются для описания волновой функции, ее производных и оператора Гамильтона.

Таким образом, оператор дифференцирования играет важную роль в физике, позволяя анализировать и описывать изменения величин и связи между ними на различных уровнях — от классической механики до квантовой физики. Без него было бы очень трудно понять и объяснить множество физических явлений и процессов, с которыми мы сталкиваемся в нашей повседневной жизни и в самой природе.

Применение оператора дифференцирования в экономике

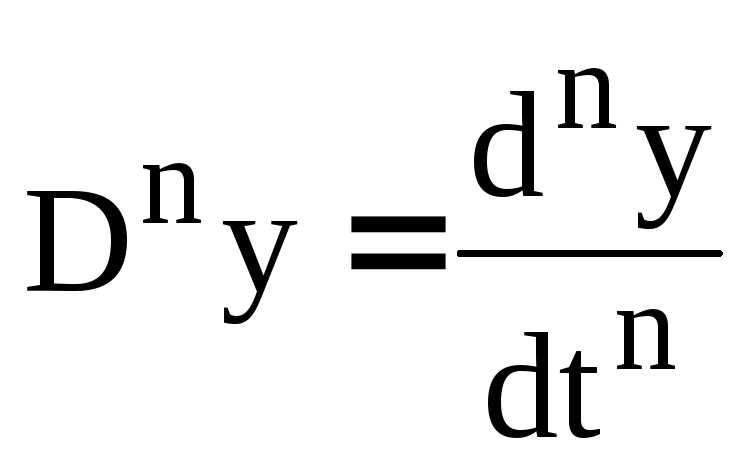
Один из ключевых аспектов применения оператора дифференцирования в экономике – это расчет эластичности переменных. Эластичность показывает, насколько процентное изменение одной переменной влияет на процентное изменение другой переменной. Например, если мы измеряем эластичность спроса по отношению к цене, то дифференцирование позволяет нам узнать, насколько процентное изменение цены повлияет на процентное изменение спроса.

Применение оператора дифференцирования также позволяет изучать тенденции и цикличность в экономических временных рядах. Экономические временные ряды представляют собой последовательность наблюдений за определенной переменной в различные моменты времени. Дифференцирование может помочь выявить тренды, сезонные колебания и циклы в таких рядах и спрогнозировать будущую динамику.

Оператор дифференцирования также применяется для анализа предельных изменений и определения оптимальных решений в экономических моделях. Например, в микроэкономике дифференцирование используется для определения предельной полезности и предельной стоимости товаров, что позволяет принять решения о потреблении и производстве на основе этих данных.

Применение оператора дифференцирования в экономике имеет широкий спектр применения, от анализа цен, спроса и предложения до моделирования и прогнозирования экономических процессов. Разработка и использование математических моделей с применением дифференцирования позволяют экономистам глубже понять сложные взаимосвязи и закономерности в экономических системах и принимать более обоснованные решения на основе этих знаний.

Применение оператора дифференцирования в статистике

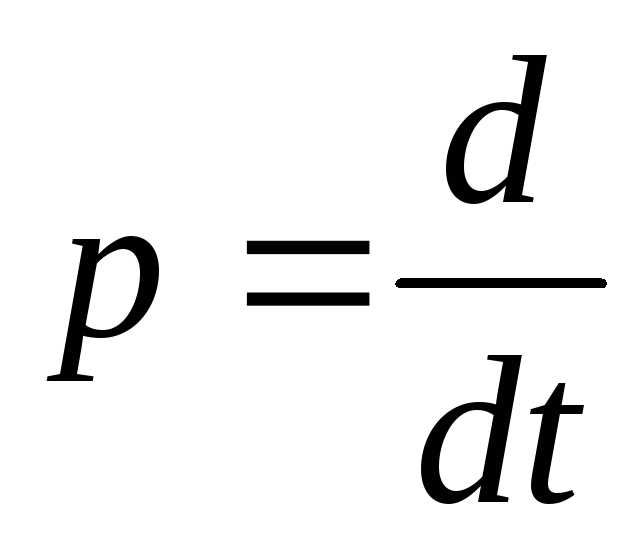
Одно из наиболее распространенных применений оператора дифференцирования в статистике – это анализ временных рядов. Временные ряды – это последовательность наблюдений за определенным явлением в разные моменты времени. Примером таких рядов могут служить данные о продажах, ценах на товары, показатели экономического роста и многое другое.

Дифференцирование временных рядов позволяет выявлять изменения трендов и сезонности. Например, если продажи товара растут с каждым месяцем, то производная временного ряда будет положительной и показывать, что рост продаж ускоряется. Наоборот, если производная отрицательна, это может указывать на замедление роста или даже снижение продаж.

Дифференцирование также позволяет выявлять экстремумы. Например, если у нас есть данные о курсе валюты в разные моменты времени, мы можем дифференцировать этот временной ряд, чтобы найти точку, в которой курс валюты достигает максимума или минимума. Это может быть полезно для прогнозирования дальнейшего поведения курса валюты.

Использование оператора дифференцирования в статистике необходимо для проведения множества анализов и прогнозов, поддерживая четкий и точный подход к обработке данных. Он позволяет находить скрытые закономерности и периодичности, разделять тренды от временных колебаний, выделять границы экстремумов. Таким образом, оператор дифференцирования в статистике играет незаменимую роль в выявлении закономерностей и понимании колебаний в данных.

Оператор дифференцирования: понятие и применение

Оператор дифференцирования обозначается символом d/dx, где d – символ дифференциации, а dx – символ переменной, по которой происходит дифференцирование.

Примеры применения оператора дифференцирования:

• Нахождение скорости изменения величины. Например, при дифференцировании функции, описывающей положение тела в пространстве по времени, получаем производную функцию, описывающую скорость.
• Нахождение касательной к графику функции в определенной точке. Производная функции в данной точке определяет наклон касательной.
• Определение точек экстремума функции. Моменты, в которых производная функции равна нулю или не существует, могут быть точками максимума или минимума функции.
• Анализ функций и исследование их свойств. Знание производных функции позволяет определить, где функция возрастает, убывает, имеет перегибы и т.д.

Оператор дифференцирования является важным инструментом в математическом анализе и широко применяется в различных научных и инженерных областях для решения задач моделирования, оптимизации, физической и экономической оценки и прочих.