Оператор в математике: определение, примеры использования и основные свойства

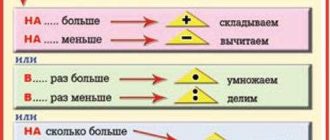
В математике оператор — это символ или знак, который выполняет определенное действие над числами или другими математическими объектами. Операторы используются для выполнения различных математических операций, таких как сложение, вычитание, умножение и деление. Они также могут выполнять более сложные действия, такие как возведение в степень или извлечение корня.

Примерами операторов являются «+», «-«, «*», «/», «^» и «√». Например, оператор «+» используется для сложения двух чисел, «-» — для вычитания, «*» — для умножения, а «/» — для деления. Оператор «^» используется для возведения числа в степень, а «√» — для извлечения квадратного корня.

Операторы имеют определенные свойства, такие как коммутативность, ассоциативность и дистрибутивность, которые позволяют проводить операции с числами в определенном порядке и получать правильный результат.

Знание операторов и их свойств является важным для понимания и решения различных математических задач и уравнений.

Определение оператора в математике

Операторы могут быть использованы в различных областях математики, таких как арифметика, алгебра, геометрия и теория вероятности. Каждый оператор имеет свою собственную функцию и правила применения.

Примеры операторов в математике

В арифметике одним из самых базовых операторов является арифметический оператор «+», который используется для сложения чисел. Например, если у нас есть числа 2 и 3, мы можем сложить их с помощью оператора «+» и получить результат 5.

Еще один пример оператора — оператор «*» (знак умножения). Он используется для перемножения чисел или других математических объектов. Например, если у нас есть числа 4 и 5, мы можем умножить их с помощью оператора «*» и получить результат 20.

Основные свойства операторов

Операторы имеют определенные свойства, которые делают их полезными инструментами в математике. Некоторые из основных свойств операторов:

• Ассоциативность: некоторые операторы ассоциативны, то есть порядок вычислений не влияет на результат. Например, оператор сложения «+» ассоциативен. Это означает, что результат сложения чисел 2 + 3 + 4 будет одинаковым, независимо от того, какой порядок сложения мы выберем.
• Коммутативность: некоторые операторы коммутативны, что означает, что порядок операндов не влияет на результат. Например, оператор умножения «*» является коммутативным. Это означает, что результат умножения чисел 2 * 3 будет таким же, как и результат умножения чисел 3 * 2.
• Распределительный закон: некоторые операторы подчиняются распределительному закону, что позволяет нам упростить выражения. Например, умножение числа на сумму двух чисел будет эквивалентно умножению этого числа на каждое из этих чисел и последующему сложению результатов.

Это только некоторые базовые свойства операторов в математике. Знание этих свойств помогает нам лучше понять и использовать операторы для решения задач и проведения вычислений.

Примеры использования операторов

1. Арифметические операторы в повседневной жизни

Арифметические операторы, такие как сложение (+), вычитание (-), умножение (*) и деление (/), широко используются в повседневной жизни. Например, когда вы покупаете товары в магазине и вычисляете итоговую стоимость покупки, вы используете арифметические операторы. Арифметические операторы также могут быть полезны в решении проблем финансового характера, таких как расчет зарплаты или определение процентного уровня скидки.

2. Логические операторы в программировании

Логические операторы, такие как И (&&), ИЛИ (||) и НЕ (!), используются в программировании для принятия решений на основе различных условий. Например, когда вы разрабатываете программу, которая должна проверять, является ли число четным или нечетным, вы можете использовать оператор «остаток от деления», чтобы определить это. Это очень полезно, когда мы хотим, чтобы наша программа принимала различные решения в зависимости от условий, которые мы устанавливаем.

3. Другие использования операторов

Операторы также используются в других сферах, таких как физика, химия, инженерия и экономика. Например, в физике операторы могут быть использованы для рассчета скорости, ускорения или силы. В экономике операторы могут быть использованы для моделирования роста или спроса. В инженерии операторы могут быть использованы для расчета сопротивления материалов или механической нагрузки на конструкцию. Во всех этих областях операторы играют ключевую роль в выполнении вычислений и принятии решений.

Оператор в математике: определение, примеры использования и основные свойства

Примеры использования операторов в математике:

• Сложение: 2 + 3 = 5
• Вычитание: 7 — 4 = 3
• Умножение: 5 * 6 = 30
• Деление: 10 / 2 = 5

Операторы в математике имеют некоторые основные свойства, которые важны для их правильного использования:

• Коммутативность: порядок операндов не влияет на результат операции. Например, a + b = b + a или a * b = b * a.
• Ассоциативность: группировка операндов не влияет на результат операции. Например, (a + b) + c = a + (b + c) или (a * b) * c = a * (b * c).
• Распределительное свойство: операция распространяется на оба операнда при выполнении операции суммы и умножения. Например, a * (b + c) = a * b + a * c.

Знание операторов и их свойств является важной основой для работы с математическими выражениями и решением математических задач.