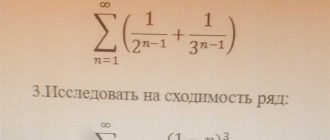Математика — это удивительная наука, которая помогает нам понять и описать законы и принципы, лежащие в основе мира. Одним из основных понятий в геометрии является прямая. Но что такое прямая и какие свойства она обладает?
Прямая — это бесконечно расширяющаяся линия, которая не имеет ни начала, ни конца. Она состоит из бесчисленного количества точек, каждая из которых является частью этой линии. Прямая также является одним из основных элементов в пространстве, в котором мы живем.
Прямая имеет несколько важных свойств. Во-первых, любые две точки на прямой можно соединить прямой линией. Во-вторых, прямая делит пространство на две части: одну справа от нее и другую слева. Наконец, прямая также является самоотносительной — она не меняется при повороте или перемещении.
Изучение свойств прямой помогает нам лучше понять мир вокруг нас и применять математические принципы в реальной жизни.
Определение
Прямая может быть представлена математически с помощью уравнения, которое связывает ее координаты на плоскости. Например, уравнение прямой может иметь вид y = mx + b, где m – это наклон прямой, а b – смещение по оси y. Каждая точка (x, y) на прямой удовлетворяет этому уравнению.
Прямая также может быть определена с помощью двух точек, через которые она проходит. Если известны координаты двух точек A(x1, y1) и B(x2, y2), можно найти уравнение прямой, проходящей через эти точки. Это называется уравнением двухточечной формы.
Одна из основных особенностей прямой – ее бесконечность. Прямая не имеет начала или конца, она простирается в обе стороны до бесконечности. Это означает, что если нарисовать любую часть прямой, всегда можно продолжить ее в обе стороны. Но чтобы работать с прямыми в математике, нам нужно использовать только определенную часть прямой.
Прямые могут пересекаться или быть параллельными друг другу. Если две прямые имеют одну общую точку, то они пересекаются. Если две прямые не имеют общих точек, то они параллельны и никогда не пересекаются. Это важное свойство прямых, которое мы можем использовать для решения задач и построения различных геометрических фигур.
Теперь мы знаем, что такое прямая и как ее можно определить математически. Понимание этого концепта поможет нам в освоении более сложных математических концепций и решении различных задач в геометрии и алгебре.
Точки на прямой
На прямой выделены различные точки, которые могут быть использованы для более точной характеристики положения объектов. Некоторые из этих точек важны по своим особенностям и приложениям в различных областях математики и науки. Давайте рассмотрим несколько таких точек и их свойства.
Главные точки на прямой:
-
Начало прямой (начало отсчета) – это точка, с которой мы начинаем измерение отрезков на прямой. Она обозначается буквой O. Начало прямой можно выбрать произвольно, в зависимости от требований задачи.
-
Конец прямой – это точка, находящаяся на прямой бесконечно далеко от начала отсчета. Она обозначается буквой E. Конец прямой также выбирается произвольно и может быть удален от начала на любое расстояние.
-
Середина отрезка – это точка, которая делит отрезок на две равные части. Например, если отрезок AB имеет точку M в середине, то AM и MB будут равными. Середина отрезка обозначается буквой M.
-
Расстояние между двумя точками – это длина отрезка, соединяющего две заданные точки на прямой. Обозначается как |AB|, где A и B – две точки.
Описанные выше точки и свойства играют важную роль в геометрии и аналитической геометрии. Они позволяют нам легче работать с прямыми, определять и измерять расстояния, а также строить различные геометрические фигуры. Их понимание и использование помогают нам лучше ориентироваться на числовой оси и анализировать пространственное расположение объектов.
Углы на прямой
Прямая линия это такая линия, которая не имеет ни начала, ни конца. Она продолжается в бесконечность и не имеет изгибов или изломов. Прямая линия одно из основных понятий в математике и широко используется в геометрии.
Когда мы говорим о прямой, нам часто приходится сталкиваться с углами, которые образуются на ней. Угол — это пространственная фигура, образованная двумя лучами, которые начинаются с общей точки, называемой вершиной угла. В контексте прямой, углы также имеют свои особенности.
Одной из основных особенностей углов на прямой является то, что они образуются только на одной стороне прямой. Если мы возьмем два луча, которые лежат по противоположные стороны от прямой, угол, образованный этими лучами, будет являться прямым углом и иметь 180 градусов.
Углы на прямой также могут быть меньше прямого угла или больше его. Углы, меньшие прямого, называются острыми углами и имеют меньше 90 градусов. Углы, большие прямого, называются тупыми углами и имеют больше 90 градусов.
Есть несколько свойств углов на прямой, которые могут помочь нам в их изучении. Например, если два угла на прямой совмещаются и образуют прямой угол, то каждый из этих углов называется смежным прямым углом. Смежные прямые углы имеют общую сторону и общую вершину.
Еще одно интересное свойство углов на прямой связано с их суммой. Сумма всех углов на прямой всегда равна 180 градусам. Это может быть полезно, когда мы хотим измерить углы, например, в геометрической фигуре или при решении математических задач.
Важно знать и понимать углы на прямой, так как они широко используются в различных областях математики и геометрии. Знание свойств углов может позволить нам решать задачи более эффективно и точно.
Пересечение прямых
Когда мы говорим о прямых, мы обычно представляем себе две линии, которые никогда не пересекаются. Но что происходит, когда прямые пересекаются? В этом случае мы говорим о пересечении прямых.
Пересечение прямых — это точка или множество точек, в которых две прямые пересекаются друг с другом. Это место, где координаты x и y двух прямых равны друг другу.
Когда мы говорим о пересечении прямых, есть несколько возможных сценариев. Возможно, прямые пересекаются в одной точке, и мы получаем решение в виде пары координат (x, y). Это называется точечным пересечением. Например, если у нас есть прямая с уравнением y = 2x + 1 и прямая с уравнением y = -x + 3, то они пересекаются в точке (1, 3).
Если прямые параллельны, то у них нет точечного пересечения. Это означает, что они никогда не пересекаются в какой-либо точке. Например, если у нас есть прямая с уравнением y = 2x + 1 и прямая с уравнением y = 2x + 3, то они параллельны, и у них нет точек пересечения.
Также возможен случай, когда прямые совпадают. Это означает, что они имеют одинаковые уравнения и, следовательно, пересекаются во всех точках. Например, если у нас есть две прямые с уравнением y = 2x + 1, то они совпадают и имеют бесконечное количество пересечений.
Пересечение прямых играет важную роль в математике и используется в различных областях. Например, в геометрии пересечение прямых может означать пересечение двух отрезков или найденные точки пересечения в координатной плоскости. В физике пересечение прямых может означать место, где два объекта встречаются в пространстве. А в экономике пересечение прямых может означать точку равновесия или оптимального решения.
Отрезки на прямой
Сегодня мы поговорим о таком интересном математическом понятии, как отрезки на прямой. Приготовьтесь к путешествию в мир геометрии и узнайте все о свойствах и определении отрезков на прямой.
Давайте начнем с определения. Отрезок на прямой — это часть прямой между двумя точками. Отметим, что точки, образующие отрезок, включаются в него. Поэтому отрезок можно изобразить как непрерывную линию, которая имеет начало и конец, обозначают его двумя точками снизу и сверху.
Отрезки на прямой могут быть разной длины. Некоторые отрезки могут быть короткими, а другие — длинными. Как определить длину отрезка? Для этого нужно измерить расстояние между точками начала и конца. Таким образом, длина отрезка на прямой — это модуль разности координат его конечных точек.
Давайте рассмотрим некоторые свойства отрезков на прямой. Первое свойство — сумма длин двух отрезков меньше или равна длине их общего отрезка. А что, если разделить отрезок на две равные части? Второе свойство гласит, что точка, делящая отрезок пополам, является его серединой.
Интересно, что отрезки могут быть перпендикулярны друг другу. Это означает, что они образуют угол в 90 градусов. И наоборот, если нас спросить, можно ли найти точку пересечения отрезков, образующих угол в 90 градусов, мы ответим, что конечно же, можно.
Мы коснулись только некоторых свойств отрезков на прямой — есть так много интересного, что можно изучать. Отрезки на прямой — это часто встречающееся понятие в геометрии, и их свойства широко применяются в различных областях науки и практической деятельности.
Теперь, когда вы знаете немного больше о отрезках на прямой, почему бы не потренироваться в их нахождении и изучении свойств? Это интересное и полезное упражнение, которое поможет вам глубже понять эту тему и улучшить математические навыки.
Ориентация прямой
Ориентация прямой означает, что мы можем определить направление движения по этой прямой. Направление может показываться стрелками, например, одной стрелкой, указывающей с одной стороны на другую, может указываться направление от наименьшего к наибольшему значению или характеристике.
Ориентация прямой часто определяется с помощью координатной оси или числовой прямой, которая отображает все значения чисел отрицательной и положительной стороной. Например, если имеется координатная ось, расположенная справа налево, то прямая, идущая слева направо, будет иметь положительную ориентацию, а прямая, идущая справа налево — отрицательную ориентацию.
Ориентация прямой также может определяться с учетом других аспектов, например, времени или физического движения. Когда мы говорим о прямой, представляющей движение, ориентация может указывать на направление движения.
Ориентация прямой может использоваться в разных областях науки и математики. Например, в физике она может указывать на направление электрического тока или вектора силы. В компьютерной графике она может определять направление объектов или осей координат на экране.
- В математике ориентация прямой играет важную роль в геометрии и алгебре. Например, она может влиять на результаты вычислений с векторами или при решении геометрических задач.
- Интересно, что ориентация прямой может быть положительной, отрицательной или нулевой. Нулевая ориентация означает, что прямая не имеет определенного направления и может двигаться в любом направлении.
Таким образом, ориентация прямой — это важный аспект, который помогает нам определить направление движения по прямой и использовать ее в различных дисциплинах. Понимание ориентации прямой может быть полезным для решения задач и анализа геометрических и математических моделей.
Одна прямая в математике: определение и свойства

Основные свойства прямой:
- Прямая является самым коротким путьом между двумя точками. Это означает, что если даны две точки, то существует только одна прямая, проходящая через эти точки.
- Любые две точки на прямой можно соединить отрезком. Отрезок является частью прямой между двумя точками, включающий эти точки и все промежуточные точки.
- Прямая делит плоскость на две полуплоскости. Все точки, лежащие на одной стороне от прямой, относятся к одной полуплоскости, в то время как точки, лежащие на другой стороне, относятся к другой полуплоскости.
- Прямая имеет бесконечное число точек. Это означает, что точки на прямой могут быть расположены очень близко друг к другу или очень далеко друг от друга.
Прямая — один из основных объектов изучаемых в геометрии. Она используется для определения других геометрических объектов, таких как отрезки, углы, треугольники и окружности. Прямые также являются основой для построения различных геометрических фигур и формулирования математических законов.