Определение координатной плоскости и ее правила

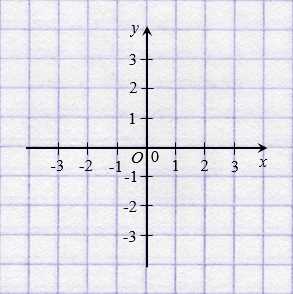
Координатная плоскость — это математическая система, которая позволяет нам определить положение точек в двумерном пространстве. Она состоит из двух осей: горизонтальной оси X и вертикальной оси Y, которые пересекаются в точке, называемой началом координат.

Правило координатной плоскости заключается в том, что каждой точке на плоскости соответствует пара чисел (x, y). Здесь x — это значение на оси X, а y — значение на оси Y. Например, точка A с координатами (3, 5) будет находиться на 3 единицы вправо от начала координат и на 5 единиц вверх от горизонтальной оси.

Координатная плоскость имеет множество применений. Она используется в геометрии для определения геометрических фигур и решения задач на площади и периметр. Она также широко применяется в физике, экономике, информатике и других областях науки и техники.

Определение координатной плоскости и правила его использования

Для описания положения точек на координатной плоскости, мы используем правило координат. Оно гласит, что каждая точка на плоскости имеет свои координаты, которые состоят из двух чисел: абсциссы (горизонтальная ось) и ординаты (вертикальная ось).

Абсцисса определяет расстояние от начала координат до некоторой точки по горизонтальной оси. Ордината определяет расстояние от начала координат до некоторой точки по вертикальной оси. Обычно, абсцисса записывается первой, затем ордината, в виде пары чисел (x, y), где x — абсцисса, y — ордината.

Прямые линии на координатной плоскости могут быть заданы в виде уравнений, которые связывают координаты точек, лежащих на этой линии. Они могут быть полезны для определения положения объекта, нахождения расстояния и других математических операций.

Чтобы лучше понять координатную плоскость и правила ее использования, можно нарисовать ее на бумаге или использовать специальные программы и считать пункты на разных уровнях или давать и адресовать их — все это поможет вам разобраться в работе с координатной плоскостью и ее правилами.

Структура координатной плоскости

Каждая точка на координатной плоскости задается парой чисел, которые называются ее координатами. Первое число в этой паре отвечает за горизонтальное положение точки и называется абсциссой. Второе число отвечает за вертикальное положение точки и называется ординатой. Например, точка A может иметь координаты (2, 3), что означает, что ее абсцисса равна 2, а ордината равна 3.

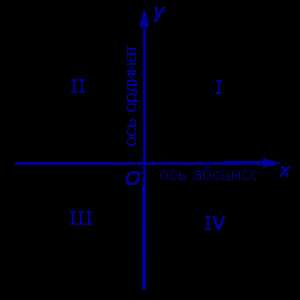
На координатной плоскости имеются оси — горизонтальная ось и вертикальная ось, которые пересекаются друг с другом в точке, которая называется началом координат. Горизонтальная ось называется осью абсцисс, а вертикальная ось — осью ординат.

Каждая ось разбивается на отрезки одинаковой длины, называемые делениями. Между делениями на оси прокладываются координатные линии, которые помогают определить координаты точек. Также на координатной плоскости обычно обозначаются числовые значения, чтобы показать, какому числу соответствует каждое деление.

Правило построения координатной плоскости

Итак, как же строить координатную плоскость? Начнем с оси абсцисс. Представьте себе горизонтальную линию, которая проходит через центр плоскости. Эта линия будет осью абсцисс. Теперь отметим на этой оси некоторые произвольные точки, которые будут служить нам знаками чисел. Обычно выбираются равноудаленные точки, чтобы облегчить чтение координат.

После того, как мы нарисовали ось абсцисс, давайте перейдем к оси ординат. Просто представьте себе вертикальную линию, которая проходит через центр плоскости. Это будет ось ординат. Подобно оси абсцисс, отметим на ней несколько точек для обозначения чисел.

И, наконец, с помощью этих двух осей можно представить числа и точки на координатной плоскости. На оси абсцисс будут представлены горизонтальные координаты, а на оси ординат — вертикальные. Когда заданы обе координаты, мы можем определить положение точки и использовать ее координаты для решения разнообразных задач и проблем.

Итак, построение координатной плоскости — это простой и интуитивный способ представления чисел и точек на плоскости. Она дает нам возможность легко работать с геометрическими и алгебраическими понятиями, а также использовать их для решения задач в различных областях.

Примеры использования координатной плоскости

Координатная плоскость находит широкое применение в различных областях знания, включая математику, физику, экономику и другие науки. Ниже приведены некоторые из примеров использования координатной плоскости:

• Графики функций: С помощью координатной плоскости можно визуализировать графики функций и изучать их свойства. Например, график функции y = x^2 будет представлять собой параболу, а график функции y = sin(x) — синусоиду.
• Геометрия: В геометрии координатная плоскость используется для изучения фигур и их свойств. Например, с помощью координат можно определить расстояние между точками, найти середину отрезка или найти точку пересечения прямых.
• Статистика: Координатная плоскость часто используется для визуализации данных в статистике. Например, диаграмма рассеяния позволяет проанализировать взаимосвязь между двумя переменными и найти возможные закономерности.
• Инженерия: В инженерии координатная плоскость применяется для моделирования и проектирования различных систем и устройств. Например, с помощью координатной плоскости можно строить схемы электрических цепей или проектировать детали механизмов.

Примеры использования координатной плоскости многочисленны и охватывают различные области. Она является важным инструментом для анализа данных, визуализации информации и решения разнообразных задач. Понимание основных принципов работы с координатной плоскостью поможет улучшить навыки в решении математических и научных задач.