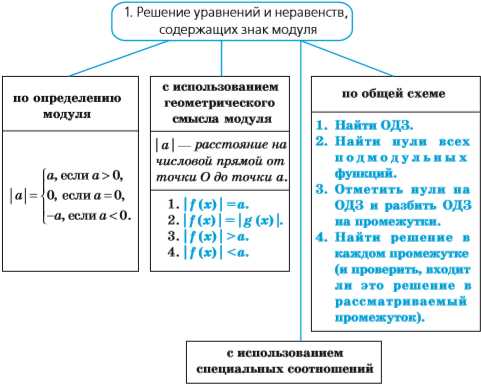
ОДЗ в математике означает «область допустимых значений». Это понятие используется для определения тех значений, которые могут принимать переменные в рамках заданного уравнения или неравенства. ОДЗ определяет, какие значения могут быть использованы для переменных, чтобы уравнение или неравенство были верными.
Например, в простом уравнении x + 2 = 5, ОДЗ для переменной x будет включать все значения, при которых x + 2 равно 5. В данном случае, x может принимать только значение 3.
Определение ОДЗ является важным инструментом для решения математических задач и проверки правильности полученных результатов.
Значение ОДЗ
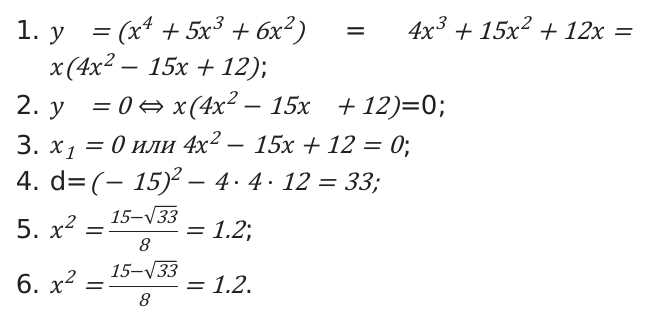
Значение ОДЗ лежит в основе понимания и решения различных математических задач. Когда мы рассматриваем функцию или переменную, ОДЗ помогает нам понять, какие значения мы можем использовать для получения верной информации или правильных результатов.
Представьте, что у вас есть функция, которая описывает зависимость между двумя переменными. Если ОДЗ не указано явно, возможны различные значения для этих переменных. ОДЗ помогает нам определить допустимые значения, чтобы функция была определена и давала смысловые результаты.
Например, если у нас есть функция, описывающая площадь прямоугольника, то ОДЗ может быть определено, чтобы ширина и длина были положительными числами. Это логично, потому что невозможно иметь отрицательную ширину или длину в реальном мире.
ОДЗ также может быть задано для переменных или функций вещественных чисел, целых чисел, натуральных чисел или дробных чисел. Каждое ОДЗ имеет свои особенности и ограничения.
Важно понимать ОДЗ, потому что она помогает избежать ошибок и противоречий в математических вычислениях и решениях. Если мы не учитываем ОДЗ при работе с переменными или функциями, мы можем получить неверные результаты или непредсказуемые значения.
Значение ОДЗ заключается в том, что оно помогает нам точно определить и использовать значения переменных и функций в математике. Оно предоставляет нам надежное исходное положение для анализа и решения задач. Без ОДЗ математическая наука стала бы менее точной, непредсказуемой и потеряла бы свою ценность в повседневной жизни и в других областях знания.
Как определить ОДЗ?

ОДЗ — это, по сути, все возможные значения, которые может принимать переменная в уравнении или неравенстве, чтобы оно имело смысл и было математически корректным. Звучит интересно, не правда ли?
Давай рассмотрим пример, чтобы все было нагляднее. Предположим, у нас есть уравнение: 2x + 3 > 5. Наша задача определить, какие значения x будут удовлетворять этому уравнению. Но как? Ведь уравнение можно решить для x и получить одно конкретное значение, а не область значений.
Подсказка: рассмотрим неравенство и применим свои математические навыки. Запомни, что при добавлении или вычитании одинакового числа с двух сторон неравенства, оно сохраняет свое значение. Как это поможет нам определить ОДЗ? Просто продолжай читать!
В нашем примере, чтобы избавиться от 3 на левой стороне неравенства, нам нужно вычесть 3 с обеих сторон. Таким образом, получим 2x > 2. Теперь поделим обе части неравенства на 2 — получим x > 1.
Вот и вся магия! Теперь мы знаем, что значение x должно быть больше 1, чтобы уравнение 2x + 3 > 5 выполнилось.
Итак, ответ на вопрос «Как определить ОДЗ?» — мы анализируем уравнение или неравенство, приводим его к более простому виду, убирая все лишнее, и из результатов определяем, какие значения переменной будут подходить. Это довольно просто, не правда ли?
Надеюсь, теперь ты чувствуешь себя увереннее в определении ОДЗ. В математике важно держать все точки над «i» и быть уверенным в каждом шаге. Приступай к решению задач с уверенностью и помни, что ОДЗ — это твои границы в мире решений математических задач!
Операции с ОДЗ
Когда мы работаем с ОДЗ, нам может потребоваться выполнить операции, такие как сложение, вычитание, умножение или деление, с выражениями или уравнениями, чтобы получить ответ или решение. При выполнении этих операций важно учитывать требования ОДЗ, чтобы избежать ошибок и получить правильный результат.
Давайте рассмотрим некоторые основные операции с ОДЗ:
- Сложение и вычитание: когда мы складываем или вычитаем выражения, важно убедиться, что ОДЗ каждого выражения совпадает, чтобы результат был корректным. Если ОДЗ одного выражения является, например, множество положительных чисел, а другого — все целые числа, мы должны сузить ОДЗ до их общего пересечения, чтобы получить правильный результат.
- Умножение: при умножении двух выражений, ОДЗ каждого из них также должно совпадать. Но в этом случае мы также должны обратить внимание на нулевые значения переменных, так как деление на ноль запрещено и может привести к некорректному значению или ошибке.
- Деление: деление является более сложной операцией в контексте ОДЗ, так как мы должны учитывать как делитель, так и делимое. Делитель не должен быть равен нулю и не должен попадать в ОДЗ, которое также запрещает его значение. Если делитель имеет ОДЗ, в котором есть ноль, мы должны исключить это значение из ОДЗ делимого, чтобы избежать деления на ноль. В этом случае мы можем сузить ОДЗ до исключения того значения, которое вызывает деление на ноль.
При выполнении операций с ОДЗ всегда важно не забывать об их требованиях и учитывать возможные ограничения переменных. Это позволит избежать ошибок и получить правильные ответы или решения задач.
Теперь, когда вы знакомы с основными операциями с ОДЗ, вы можете более уверенно решать задачи и уравнения, учитывая их возможные ограничения и требования. Постоянная практика и применение этих знаний позволят вам стать более квалифицированным в решении математических задач и достичь успеха в обучении.
Примеры ОДЗ
- Дробная функция: f(x) = 1 / (x — 2)
- Корневая функция: g(x) = √(x — 5)
- Логарифмическая функция: h(x) = log(x + 3)
- Тригонометрическая функция: k(x) = sin(x)
Ограничения по ОДЗ для данной функции заключаются в избегании деления на ноль и области, где знаменатель равен нулю. В данном случае ОДЗ будет следующее: x ≠ 2.
Для корневой функции ОДЗ должна обеспечивать неотрицательное значение подкоренного выражения. В нашем случае ОДЗ будет выглядеть так: x — 5 ≥ 0, что можно представить как x ≥ 5.
Логарифмическая функция определена только для положительных аргументов, поэтому ОДЗ для данной функции можно записать как x + 3 > 0, или, исключив дополнительное слагаемое x > -3.
Тригонометрические функции также имеют свои ограничения. Например, функция синуса периодическая и принимает значения в интервале [-1, 1]. Таким образом, ОДЗ для функции sin(x) будет просто -∞ < x < +∞.
Все эти примеры ОДЗ показывают, что в математике очень важно определить, в каких пределах функция определена и допустима, чтобы избежать ошибок и недопустимых операций. Поэтому необходимо внимательно анализировать ОДЗ при работе с математическими функциями и уравнениями.
Свойства ОДЗ
ОДЗ обладает несколькими важными свойствами, которые помогают нам решать математические задачи:
1. Единственность ОДЗ
Каждое математическое выражение или уравнение имеет только одну ОДЗ. Это означает, что есть определенный набор значений, которые можно присвоить переменным в выражении, чтобы оно было корректным. Если переменная может иметь несколько ОДЗ, то это означает, что она может принимать разные значения, в зависимости от контекста задачи.
2. Включение ОДЗ в другие ОДЗ
ОДЗ может быть включена в другую ОДЗ. Это означает, что если некоторое значение принадлежит одной ОДЗ, то оно будет принадлежать и другой. Например, если ОДЗ для переменной x состоит из всех чисел больше 5, то значит, что все числа больше 10 также принадлежат ОДЗ для переменной x. Это свойство очень полезно при решении задач, поскольку позволяет нам получать более точные результаты.
3. Исключение значений в ОДЗ
ОДЗ может исключать определенные значения или диапазоны значений. Например, если ОДЗ для переменной x состоит из всех чисел, кроме 5, это означает, что значение 5 не допустимо для переменной x. Это свойство позволяет нам определять ограничения для переменных и устанавливать условия, необходимые для правильного решения задачи.
4. ОДЗ может быть бесконечным
ОДЗ может содержать бесконечное количество значений. Например, ОДЗ для переменной x может состоять из всех действительных чисел. Это означает, что переменная x может принимать любое значение из этого диапазона. Бесконечность ОДЗ позволяет нам решать широкий спектр задач и строить точные модели в математике.
Определение области допустимых значений (ОДЗ) в математике
Определение ОДЗ имеет важное значение в математике, так как позволяет ограничить диапазон значений переменных или функций, в которых выражение имеет смысл. Отрицание условий ОДЗ может привести к делению на ноль, извлечению квадратного корня из отрицательного числа или другим недопустимым операциям.
Одним из способов определения ОДЗ является анализ знаменателя в выражении или функции. Если знаменатель равен нулю, то это означает, что выражение или функция не определены в данной точке или интервале. В таком случае, ОДЗ будет состоять из всех значений переменных или функций, при которых знаменатель не равен нулю.
ОДЗ может быть описана с помощью интервалов, множества точек или других математических обозначений. Например, ОДЗ может быть записано в виде (-∞, 0) U (0, +∞), что означает, что значение переменной должно быть меньше нуля или больше нуля, но не может быть равно нулю.