Определение равных векторов в геометрии. Урок для 9 класса

Основные понятия векторов

Захотите ли вы перенести предмет с одной точки на другую? Конечно, да! Ну, вот векторы нам в этом помогают. Они позволяют нам определить начало и конец перемещения и указать направление и длину этого перемещения. Векторы представляют собой стрелки, которые указывают на то, какой путь нужно пройти, чтобы достичь конечной точки.

Каждый вектор состоит из двух ключевых частей: направление и длина. Направление показывает, куда вектор указывает, а длина указывает, насколько далеко нужно двигаться. Направление обычно указывается с помощью угла относительно какой-то фиксированной оси, например, горизонтальной оси.

Если векторы имеют одинаковое направление и равные длины, то они считаются равными. Например, рассмотрим два вектора, первый со стрелкой вниз и длиной 3, а второй с той же стрелкой вниз и длиной 3. Оба вектора указывают вниз и имеют одинаковую длину, следовательно, они равны. Как вы думаете, можно ли сказать, что эти векторы представляют одно и то же движение или разные?

Также векторы могут быть сложены или вычитаны. При сложении векторов мы просто помещаем их концы вместе и рисуем новый вектор от начала первого вектора до конца второго вектора. Результатом будет вектор, который указывает на новое положение.

Векторы являются незаменимым инструментом для изучения мира вокруг нас. Используя их, мы можем анализировать и объяснять различные физические явления, предсказывать направление и скорость движения различных объектов и даже решать геометрические задачи.

Так что следующий раз, когда вы увидите стрелку, задумайтесь о векторах и их роли в нашей жизни. Узнайте, куда она указывает и представьте, какую роль она может сыграть в определении движения или направления.

Условие равенства векторов

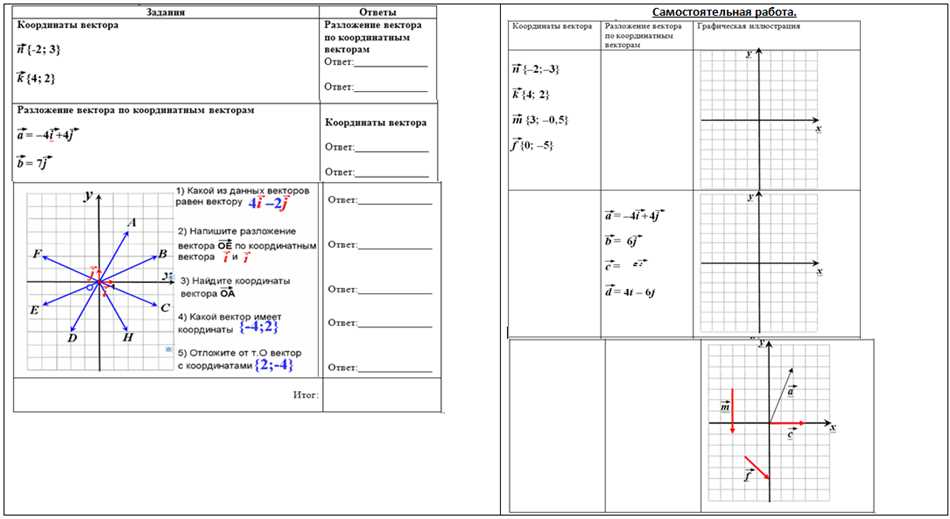
Прежде всего, векторы должны иметь одинаковую длину. Это означает, что расстояние от начала одного вектора до его конца должно быть равно расстоянию от начала второго вектора до его конца. Если два вектора имеют разные длины, то они не могут быть равными.

Кроме того, у векторов должны быть равными все их составляющие. Векторы состоят из координат, которые определяют их направление и величину. Если у двух векторов все координаты совпадают, то они считаются равными.

Однако равенство векторов может быть проверено не только по их длине и координатам. Оно также может быть проверено с помощью операций над векторами. Например, если для двух векторов выполняется операция сложения и результат совпадает, то векторы считаются равными.

Также при умножении векторов на скаляр, если результат равен для двух векторов, то они также считаются равными.

Это условие равенства векторов играет важную роль в геометрии. Поиск равных векторов позволяет нам определить симметрию, параллельность и другие важные свойства фигур и физических систем.

Геометрическое определение равенства векторов

Теперь представьте, что у вас есть 2 вектора — один отображает расстояние, которое вы прошли, а другой — расстояние, которое вы планируете пройти на карте. Если они имеют одинаковую длину и направление, то мы можем сказать, что эти векторы равны.

Таким образом, геометрическое определение равенства векторов заключается в том, что два вектора считаются равными, если они имеют одинаковую длину и направление.

Важно понимать, что равенство векторов не зависит от их положения в пространстве или начала координат. Другими словами, если два вектора имеют одинаковую длину и направление, они равны, даже если они начинаются из разных точек или находятся в разных частях пространства.

Чтобы лучше представить себе это определение, давайте рассмотрим пример.

Представьте, что у вас есть вектор А, направленный на восток со значением (2, 0), и вектор В, также направленный на восток, но со значением (4, 0). Очевидно, что оба вектора имеют одинаковое направление и длину, поэтому они равны.

Теперь представьте, что у вас есть вектор С, направленный на юг с значением (0, -3), и вектор D, тоже направленный на юг, но со значением (0, -5). Опять же, оба вектора имеют одинаковое направление и длину, поэтому они равны.

Таким образом, геометрическое определение равенства векторов позволяет нам определить, когда два вектора равны, основываясь на их направлении и длине.

Операции с векторами

В геометрии векторами называются направленные отрезки с определенной длиной. Векторы обладают определенными свойствами и могут подвергаться различным операциям. Давайте рассмотрим основные операции с векторами.

Сложение векторов

Одной из основных операций с векторами является их сложение. Сумма двух векторов получается приложением начала одного вектора к концу другого вектора. Итоговый вектор будет являться диагональю параллелограмма, образованного исходными векторами.

Пример: у вас есть векторы AB и BC. Чтобы получить вектор AC, нужно приложить вектор BC к концу вектора AB.

Умножение вектора на число

Еще одной важной операцией с векторами является умножение вектора на число. При умножении на положительное число длина вектора увеличивается, а его направление не изменяется. Когда вектор умножается на отрицательное число, его направление меняется, но его длина остается такой же. Эта операция также называется скалярным умножением вектора.

Пример: если у вас есть вектор AB, и вы умножаете его на 2, то получаете вектор AB с удвоенной длиной, но с тем же направлением.

Вычитание векторов

Вычитание векторов — это операция, обратная сложению векторов. Разность двух векторов получается приложением начала одного вектора к концу другого вектора, но с противоположным направлением исходного вектора.

Пример: у вас есть векторы AB и BC. Чтобы получить вектор AC, нужно приложить вектор BC к концу вектора AB, но в обратном направлении.

Равенство векторов

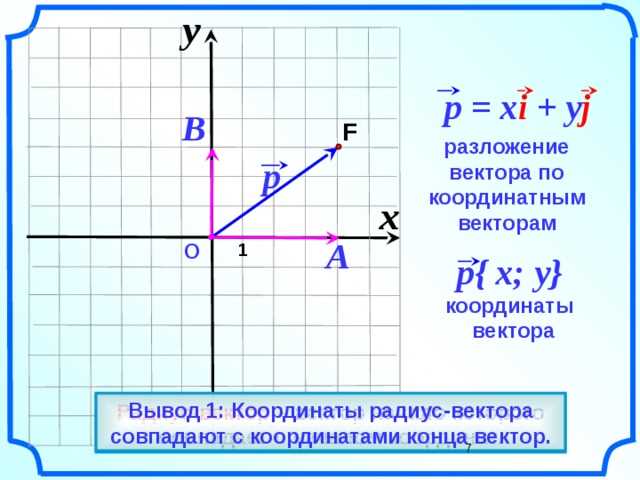
Два вектора считаются равными, если они имеют одинаковую длину и направление. То есть, если два вектора указывают в одну и ту же сторону и имеют одинаковую длину, они считаются равными.

Пример: если у вас есть вектор AB длиной 3 и вектор CD длиной 3, направленный в ту же сторону, то эти векторы равны.

Векторы — это очень полезный инструмент в геометрии. Изучение операций с векторами поможет вам лучше понять их свойства и применение в решении геометрических задач.

Определение равных векторов в геометрии. Урок для 9 класса

Предположим, у нас есть два вектора: вектор А и вектор В. Чтобы проверить, являются ли они равными, мы сравниваем их длины и направления. Если длины и направления векторов совпадают, то они являются равными векторами. Для удобства записи равных векторов мы используем символ «≡» между двумя векторами.

Например, если вектор А имеет длину 5 и направление вверх, а вектор В имеет длину 5 и направление вверх, то мы можем записать это в виде «А ≡ В«, что означает, что вектор А равен вектору В.

Если же длины или направления векторов отличаются, то они являются неравными векторами. Например, если вектор А имеет длину 5 и направление вверх, а вектор В имеет длину 5 и направление вниз, то мы можем записать это как «А ≠ В«, что означает, что вектор А не равен вектору В.

Правила сравнения векторов для определения их равенства:

• Для равенства векторов необходимо чтобы у них совпали модули (длины) и направления.
• Векторы, которые только попарно совпадают по направлению, не являются равными, так как их длины могут отличаться.
• Если длины векторов равны, но направления отличаются, то векторы также не являются равными.

Получившиеся правила позволяют убедиться в равенстве или неравенстве векторов путем сравнения их длин и направлений. Знание этих правил поможет нам в решении задач по геометрии и анализу векторов.