Определенный и неопределенный интеграл: различия и понятие

Интегралы — одна из важнейших тем в математике, которая позволяет решать широкий спектр задач. Существуют два основных типа интегралов: определенный и неопределенный.

Неопределенный интеграл — это интеграл без указания верхнего и нижнего пределов. Он является обратной операцией к дифференцированию и позволяет найти функцию, производная которой является исходной функцией. Неопределенный интеграл обозначается символом ∫.

Определенный интеграл — это интеграл, в котором указаны верхний и нижний пределы интегрирования. Он показывает площадь под кривой графика функции на заданном интервале. Определенный интеграл обозначается символом ∫ с указанием пределов интегрирования.

В данной статье рассмотрим подробнее понятие и различия между определенным и неопределенным интегралами.

Определение интеграла

Итак, что же такое интеграл? В общем смысле, интеграл означает нахождение площади под кривой, вычисление суммы бесконечного числа бесконечно малых величин, или нахождение обратной функции к производной.

Определенный интеграл

Давайте начнем с определенного интеграла. Он используется для вычисления площади под графиком функции на заданном интервале. Другими словами, определенный интеграл позволяет найти значение функции в определенном диапазоне переменной.

Прежде чем перейти к формулам, давайте проясним это на примере. Представьте себе график функции, отображающей движение автомобиля. Определенный интеграл позволит нам вычислить общее пройденное расстояние автомобиля на заданном интервале времени.

Математически определенный интеграл записывается следующим образом:

∫_a^b f(x) dx = F(b) — F(a),

где ∫ – знак интеграла; a и b – границы интегрирования; f(x) – подынтегральная функция; F(x) – интеграл от функции f(x). Это определение позволяет нам оценить площадь под графиком на заданном интервале и найти значение функции на этом интервале.

Неопределенный интеграл

Теперь давайте перейдем к неопределенному интегралу. В отличие от определенного интеграла, неопределенный интеграл не имеет верхней или нижней границы интеграции. Он позволяет нам найти общую антипроизводную функции, то есть искать функцию, производная которой равна подынтегральной функции.

Примером неопределенного интеграла может быть:

∫ f(x) dx = F(x) + C,

где C – постоянная, называемая постоянной интегрирования.

Неопределенный интеграл позволяет нам находить аналитическое выражение для функции, что позволяет проводить дальнейшие операции с ней и использовать в различных задачах.

Заключение

Итак, определенный и неопределенный интегралы имеют различные определения и применяются для решения разных задач. Определенный интеграл помогает найти площадь под графиком функции на заданном интервале, а неопределенный интеграл позволяет находить аналитическое выражение для функции. Оба эти интеграла являются важными инструментами математического анализа и они находят широкое применение в науке, инженерии, физике и многих других областях.

Определенный интеграл

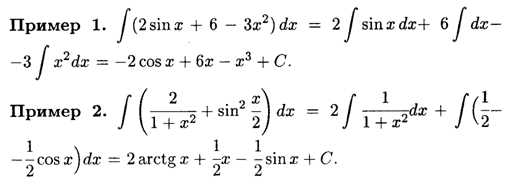
Интеграл – это математическая операция, являющаяся обратной к дифференцированию. Если дифференцирование позволяет найти скорость изменения функции, то интегрирование позволяет найти саму функцию по её скорости изменения.

Определенный интеграл — это частный случай интеграла, в котором находят не просто функцию, а значение функции на заданном отрезке.

Для вычисления определенного интеграла используется символ «∫», который означает интеграл. Определенный интеграл обозначается так:

∫_a^b f(x)dx

• a — это нижний предел интегрирования, то есть начальная точка отрезка;
• b — это верхний предел интегрирования, то есть конечная точка отрезка;
• f(x) — это подынтегральная функция, то есть функция, которую интегрируют;
• dx — это дифференциал переменной, по которой интегрируют.

Определенный интеграл можно интерпретировать как площадь фигуры, ограниченной графиком функции, осью OX и прямыми x=a и x=b. То есть, это площадь под кривой на заданном отрезке.

Получить точное значение определенного интеграла можно с помощью различных методов численного интегрирования, однако в некоторых случаях он может быть выражен аналитически. Например, интеграл от постоянной функции равен произведению этой функции на разность верхнего и нижнего пределов интегрирования:

∫_a^b cdx = c(b-a)

Определенный интеграл имеет множество приложений в различных областях науки, например, в физике для нахождения центра масс тонкого листа или объема тела, а также в экономике для определения площади под кривой спроса или предложения на рынке.

Таким образом, определенный интеграл является мощным инструментом для вычисления площадей и нахождения средних значений функций, что делает его неотъемлемой частью математического анализа и других научных дисциплин.

Неопределенный интеграл

Именно для решения таких задач и возникла математическая область, называемая интегралом. Интеграл – это мощный математический инструмент, который позволяет находить площадь фигур не только с прямоугольной формой, но и с самыми разнообразными и сложными контурами.

Различают два вида интегралов: неопределенный и определенный. Сегодня мы поговорим об неопределенном интеграле.

Неопределенный интеграл – это интеграл, у которого не указаны границы интегрирования. В отличие от определенного интеграла, который находит площадь ограниченной фигуры на заданном интервале, неопределенный интеграл находит некую функцию, производной которой является исходная функция.

Возьмем, например, функцию f(x) = 2x. Наша задача – найти функцию F(x), производной которой является функция f(x). То есть мы ищем такую функцию F(x), у которой производная F'(x) равна 2x.

Подумайте, какая функция может удовлетворить этому условию? Вспомните, что при нахождении производной функции, мы избавлялись от постоянных коэффициентов и превращали степень в коэффициент. Таким образом, следуя обратному пути, мы можем сказать, что функция F(x) должна иметь вид F(x) = x^2 + C, где С – произвольная постоянная.

То есть, неопределенный интеграл от функции f(x) = 2x будет равен F(x) = x^2 + C, где F'(x) = 2x.

Позвольте мне задать вам вопрос: Как вы себя чувствуете, осознавая, что вы только что узнали об одной из мощных математических техник, которая позволяет найти функцию, производной которой является исходная функция? Уверенно, не так ли?

Если у вас возникли вопросы или сомнения, не стесняйтесь – задавайте их в комментариях или в следующем уроке. Вместе мы сможем разобраться во всех тонкостях неопределенного интеграла и стать настоящими мастерами математики!

Свойства интеграла

1. Линейность

Интеграл обладает свойством линейности, то есть сумма или разность интегралов от двух функций равна интегралу от суммы или разности этих функций. Например, если такие функции f(x) и g(x) имеют определенный интеграл на каком-то отрезке, то интеграл от их суммы или разности на этом отрезке будет равен сумме или разности соответствующих интегралов.

2. Аддитивность

Интеграл также обладает свойством аддитивности, то есть интеграл от функции на объединении нескольких непересекающихся отрезков равен сумме интегралов на этих отрезках. Например, если f(x) имеет определенный интеграл на двух отрезках [a, b] и [b, c], то интеграл от функции f(x) на отрезке [a, c] будет равен сумме интегралов на отрезках [a, b] и [b, c].

3. Производная и интеграл

Есть тесная связь между понятием производной и интеграла. Если функция f(x) имеет производную на некотором отрезке, то интеграл от нее на этом отрезке будет равен приращению этой функции на этом отрезке. И наоборот, если интеграл функции равен приращению этой функции на некотором отрезке, то функция имеет производную на этом отрезке.

4. Интеграл и площадь

Интеграл можно интерпретировать как площадь под графиком функции. Это означает, что интеграл от неотрицательной функции на некотором отрезке равен площади фигуры, ограниченной графиком этой функции и осью абсцисс на этом отрезке.

5. Замена переменной

Интеграл может быть вычислен методом замены переменной. Это свойство очень полезно в случаях, когда функция не поддается прямому интегрированию, но может быть приведена к другому виду с помощью подходящей замены переменной. Замена переменной позволяет привести интеграл к более простому виду и упростить его вычисление.

Таким образом, свойства интеграла позволяют нам удобно и эффективно работать с данной математической операцией. Они дают нам возможность линейно комбинировать интегралы, вычислять их на различных отрезках, использовать связь между интегралом и производной, интерпретировать интеграл как площадь и применять метод замены переменной для упрощения вычислений.

Различия между определенным и неопределенным интегралом

Определенный интеграл – это интеграл, в котором заданы верхний и нижний пределы интегрирования. Он позволяет найти площадь ограниченной фигуры под кривой, а также считает сумму значений функции на определенном промежутке. Чтобы рассчитать определенный интеграл, необходимо знать точные значения нижнего и верхнего пределов, а также функцию, под которой происходит интегрирование.

Неопределенный интеграл – это интеграл, в котором не указаны верхний и нижний пределы интегрирования. Он позволяет найти общий вид функции, которая была проинтегрирована. Результатом неопределенного интеграла является функция, полученная с помощью выполнения операции интегрирования над исходной функцией. Для вычисления неопределенного интеграла необходимо знать только интегрируемую функцию, а точные значения пределов интегрирования не требуются.

Таким образом, можно сказать, что основное различие между определенным и неопределенным интегралом заключается в наличии или отсутствии пределов интегрирования. Определенный интеграл используется для вычисления численных результатов с учетом верхнего и нижнего пределов, тогда как неопределенный интеграл позволяет получить функцию источник, проинтегрировав которую.

Теперь, когда мы разобрались в различиях между определенным и неопределенным интегралом, давайте рассмотрим их применение в реальной жизни. Как бы вы использовали эти интегралы в своей работе или исследованиях? Какие задачи вы могли бы решить, используя эти инструменты? Поделитесь своими мыслями!

Определенный и неопределенный интеграл: понятие и различия

Неопределенный интеграл

Неопределенный интеграл — это процесс нахождения первообразной функции. Первообразная функция — это функция F(x), чья производная равна заданной функции f(x). Математически записывается как:

∫ f(x) dx = F(x) + C

где dx — бесконечно маленькое приращение переменной x, C — постоянная интегрирования (константа).

Неопределенный интеграл может быть выражен с использованием символа интеграла (∫), который означает процесс интегрирования.

Определенный интеграл

Определенный интеграл — это численное значение интеграла на заданном интервале. Он обозначается следующим образом:

∫_a^b f(x) dx = F(b) — F(a)

где a и b — концы интервала интегрирования, F(a) и F(b) — значения первообразной функции на концах интервала.

Определенный интеграл вычисляется путем нахождения значения функции на концах интервала, нахождения разности этих значений и взятия модуля от полученного результата (площадь под кривой может быть и отрицательной).

Различия между неопределенным и определенным интегралом

• Неопределенный интеграл находит первообразную функцию, а определенный интеграл находит численное значение интеграла на заданном интервале.
• Неопределенный интеграл выражается с помощью символа интеграла, а определенный интеграл обозначается через интервал интегрирования.
• Неопределенный интеграл имеет постоянную интегрирования, которая не присутствует в определенном интеграле.
• Определенный интеграл вычисляется численно, а для неопределенного интеграла используется то же математическое выражение, которое находит первообразную функцию.