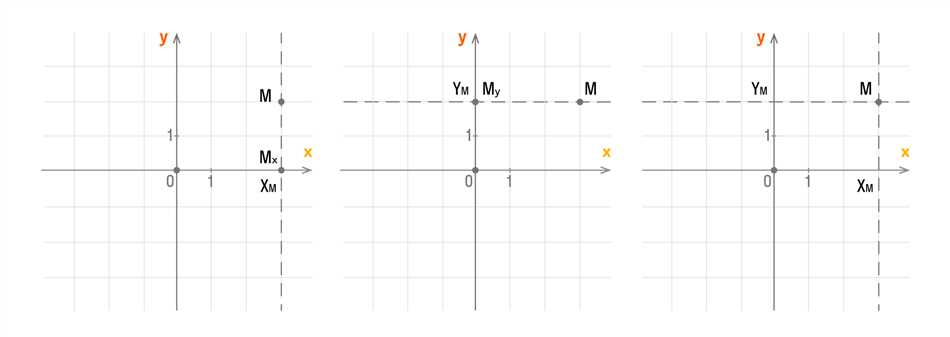
Когда мы говорим о алгебре, невозможно не обратить внимание на два важных понятия — ординату и абсциссу. Они являются основой для графического представления функций и явлений в алгебре. Вероятно, каждый из нас хотя бы раз сталкивался с этими терминами в школьной программе или учебниках. И, может быть, даже слышал о них в повседневной жизни. Но что они означают на самом деле и как они применяются?
Ордината — это вертикальная ось на графике, которая показывает значение функции или переменной. Она обычно помечается числами и позволяет представить, как меняется значение функции при изменении аргумента.
Абсцисса — это горизонтальная ось на графике, которая показывает значение аргумента функции. Также помечается числами и помогает нам определить, насколько изменяется значение функции при изменении аргумента.
Знание этих понятий позволяет нам лучше понимать и анализировать графики функций, строить математические модели и решать задачи. Погрузимся в мир алгебры и узнаем больше о роли ординаты и абсциссы в алгебре.
Определение ординаты
Ордината измеряет вертикальное расстояние от точки до начала координатной системы или до оси абсцисс. Она может принимать значения как в положительной, так и в отрицательной области.
В алгебре ордината используется для решения уравнений, построения графиков и анализа функций. Например, при построении графика линейной функции, значения ординаты определяются по формуле y = mx + b, где m — наклон прямой, а b — свободный член.
Ордината имеет широкое применение в различных областях науки и техники. Например, в физике ордината может представлять силу, ускорение или положение тела в пространстве. В экономике она может обозначать объем продаж или прибыль.
Понимание ординаты позволяет решать различные математические задачи и улучшает понимание процессов, происходящих на плоскости. Знание этого понятия открывает перед нами мир математического моделирования и анализа, позволяет видеть закономерности и предсказывать результаты.
Определение абсциссы
Абсцисса представляет собой горизонтальную ось, которая перпендикулярна к вертикальной оси, называемой ординатой. Вместе они образуют декартову систему координат, которая позволяет нам точно определить положение любой точки на плоскости. Абсцисса используется для измерения расстояния между точкой и вертикальной осью.
Абсцисса обозначается буквой «х» и может принимать различные значения, в зависимости от положения точки на плоскости. Если точка находится выше вертикальной оси, ее абсцисса будет положительной. Если точка находится ниже вертикальной оси, ее абсцисса будет отрицательной.
Определение абсциссы играет важную роль в алгебре и геометрии. Она помогает нам решать уравнения, строить графики функций и решать геометрические задачи. Знание определения абсциссы также поможет вам лучше понимать и применять математические концепции в повседневной жизни.
Связь ординаты и абсциссы с координатами точки на плоскости
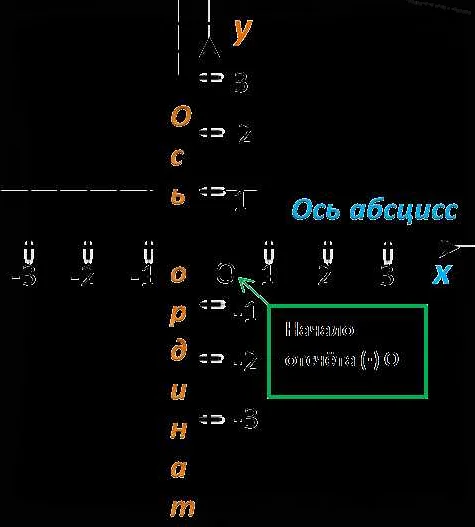
Координатная плоскость состоит из двух осей — горизонтальной оси, которая называется абсциссой, и вертикальной оси, которая называется ординатой. По сути, координаты точки на плоскости представляют собой пару чисел, где первое число отражает расстояние точки от вертикальной оси (ординаты), а второе число — расстояние от точки до горизонтальной оси (абсциссы).
Например, предположим у нас есть точка A с координатами (2, 3) на координатной плоскости. Здесь число 2 представляет расстояние от точки A до оси ординат, а число 3 — расстояние от точки A до оси абсцисс.
Визуально, координаты точек на плоскости можно представить с помощью сетки из перпендикулярных линий, где каждая линия соответствует определенному значению абсциссы или ординаты. Пересечение этих линий образует определенную точку.
Зачем нам нужна связь между ординатой, абсциссой и координатами точки на плоскости? С помощью координат мы можем выполнять различные операции, такие как нахождение расстояния между точками, определение углов и даже построение графиков. Имея координаты точки, мы можем легко распознать ее положение и выполнять все необходимые вычисления.
Таким образом, ордината и абсцисса являются ключевыми элементами в определении положения точки на плоскости. Они позволяют нам представить координаты точек в числовой форме и производить различные вычисления и операции с этими точками.
Графическое изображение ординаты и абсциссы
Когда мы говорим о графическом изображении ординаты и абсциссы, мы имеем в виду построение графика, в котором ось ординат представлена вертикальной линией, а ось абсцисс — горизонтальной. На этом графике мы можем отображать различные точки и их координаты.
Графическое изображение ординаты и абсциссы — это мощный инструмент для понимания и анализа различных математических функций и соотношений. Например, если мы хотим изучить зависимость между временем и расстоянием, мы можем отобразить время на горизонтальной оси (абсциссе) и расстояние на вертикальной оси (ординате).
Графическое изображение ординаты и абсциссы позволяет нам легко увидеть, какие точки соответствуют определенным значениям ординаты и абсциссы. Мы можем строить линии, кривые и другие графические элементы, чтобы визуально представить различные функции и их свойства.
С помощью графического изображения ординаты и абсциссы мы можем решать различные математические задачи и исследовать различные функции и уравнения. Например, мы можем определить точки пересечения двух графиков или найти максимум или минимум функции.
Применение ординаты и абсциссы в геометрии
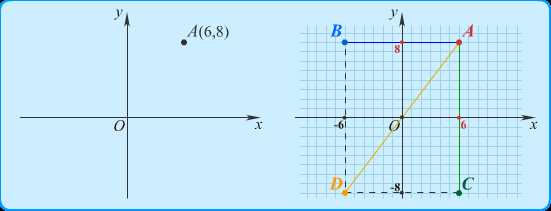
Ордината — это значение по оси Y, которое позволяет определить вертикальное положение точки на плоскости или в пространстве. Ординату обозначают буквой Y или y. Например, если мы говорим о точке P, то ордината этой точки обозначается как P(Y) или P(y).
Абсцисса, в свою очередь, представляет собой значение по оси X и определяет горизонтальное положение точки на плоскости или в пространстве. Абсциссу обозначают буквой X или x. Если речь идет о точке R, то ее абсцисса будет обозначаться как R(X) или R(x).
Применение ординаты и абсциссы в геометрии очень широко. Например, они позволяют нам находить расстояние между двумя точками на плоскости. Для этого мы используем формулу расстояния между точками, в которой используются и ордината, и абсцисса.
Ордината и абсцисса также позволяют нам строить различные геометрические фигуры и определять их свойства. Например, если мы знаем координаты трех точек на плоскости, то с помощью ординаты и абсциссы мы можем определить, образуют ли эти точки прямую, треугольник или какую-либо другую фигуру.
Кроме того, ордината и абсцисса используются в геометрии для нахождения центра и радиуса окружности, а также для определения углов наклона прямых или плоскостей.
Наконец, ордината и абсцисса играют важную роль в аналитической геометрии. С их помощью мы можем решать уравнения, строить графики функций и исследовать их свойства. Например, график функции y = f(x), где f — функция, представляет собой совокупность точек (x, y), где x — абсцисса, а y — ордината.
Таким образом, ордината и абсцисса являются важными понятиями в геометрии и имеют широкое применение в решении различных задач. Они помогают нам определить положение точек на плоскости или в пространстве, строить фигуры, находить расстояния, исследовать графики функций и многое другое. Понимание этих понятий и их применение позволяют нам лучше разбираться в геометрии и алгебре, а также применять их в решении различных задач и проблем.
Ордината и абсцисса в алгебре: понятия и применение
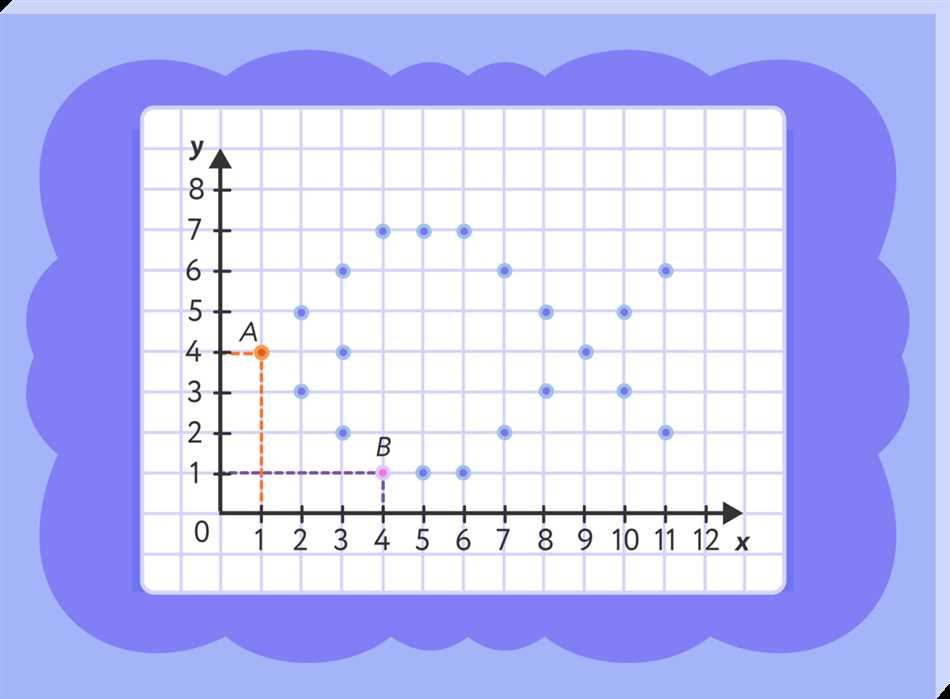
Абсцисса точки – это расстояние по горизонтали от начала координатной системы (начала оси абсцисс) до точки. Ордината точки – это расстояние по вертикали от начала координатной системы (начала оси ординат) до точки.
В алгебре координаты точек на плоскости помогают нам решать различные задачи и строить графики функций. Координаты точек могут быть представлены числами или переменными.
Например, если у нас есть точка A с координатами (3, 4), то 3 будет являться абсциссой этой точки, а 4 – ординатой. По аналогии, точка B с координатами (-2, -5) будет иметь абсциссу -2 и ординату -5.
С помощью координат точек на плоскости мы можем строить графики функций. График функции – это множество точек на плоскости, координаты которых удовлетворяют уравнению функции.
Например, график функции y = x^2 будет выглядеть как парабола, потому что каждая точка на этом графике будет иметь координаты (x, x^2).
Таким образом, понимание понятий ординаты и абсциссы в алгебре позволяет нам более удобно работать с геометрическими объектами и решать задачи, связанные с алгеброй и графиками функций.





