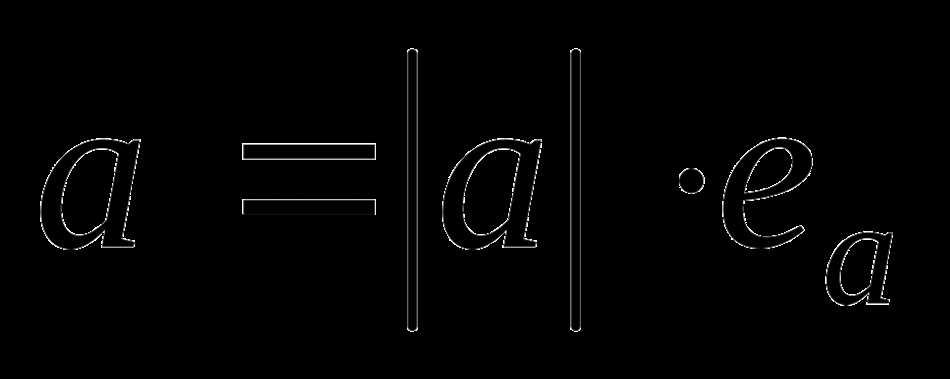
Орт вектор: определение, свойства и применение

Орт вектор — это вектор, который обладает особым свойством – он ортогонален, или перпендикулярен, другим векторам. Такой вектор имеет длину равную единице и выбран таким образом, чтобы его направление было перпендикулярно к плоскости или пространству. Орт векторы играют важную роль во многих областях, включая физику, математику, компьютерную графику, механику и другие. Они помогают в решении задач, связанных с расчетами, анализом и визуализацией различных объектов и явлений. В данной статье мы рассмотрим определение, свойства и применение орт векторов более подробно.

Орт вектор: определение

Итак, что же такое орт вектор? Вектор, само собой, представляет собой направленный отрезок, имеющий длину и направление. Казалось бы, векторы — это уже достаточно интересная и полезная концепция. Но вот когда в дело вступает орт, все становится еще интереснее.

Орт вектор — это вектор, который обладает особым свойством: его длина равна 1. Да, именно так! Вообрази множество векторов, разных по направлению и длине. И теперь из этого множества выбери такие векторы, длина которых будет равна 1. И это будут орт векторы!

Ты, наверное, задаешься вопросом: «А зачем вообще нужны орт векторы?». Отличный вопрос! Орт векторы играют очень важную роль во многих областях науки и техники. Например, они широко используются в физике, компьютерной графике, робототехнике и многих других областях. Они помогают нам описывать и анализировать различные явления и моделировать их поведение.

Но важно помнить, что орт векторы не только имеют длину равную 1, они также должны быть ортогональными, то есть перпендикулярными друг другу. Обрати внимание на это свойство орт векторов, оно часто играет ключевую роль в расчетах и анализе данных.

Теперь, когда мы знакомы с определением орт вектора, давай подытожим! Орт вектор — это вектор, длина которого равна 1 и который перпендикулярен к другим векторам. Они широко используются в науке и технике, помогая нам лучше понять и анализировать мир вокруг нас. И если тебе когда-нибудь придется столкнуться с орт векторами, ты уже знаешь, что они представляют и почему они так важны.

Так вот, уважаемый читатель, ты теперь владеешь знаниями о понятии орт вектора. Не забывай применять их на практике и вдохновляться всеми необычными и красивыми свойствами орт векторов. И помни, что математика и наука в целом — это великое приключение!

Свойства орт вектора

• Единичная длина: Одним из ключевых свойств орт вектора является то, что его длина равна единице. Это означает, что каждый компонент вектора имеет размер, равный или близкий к 1. Благодаря этому свойству орт вектора, мы можем использовать его для измерения и представления физических величин, таких как направление движения или координаты точки в пространстве.
• Перпендикулярность: Орт векторы являются перпендикулярными друг другу. Это означает, что при их суммировании или вычитании мы получаем вектор, перпендикулярный им обоим. Такое свойство орт векторов позволяет использовать их для решения геометрических задач, таких как определение угла между двумя линиями или нахождение пересечения двух плоскостей.
• Линейная независимость: Орт векторы являются линейно независимыми. Это означает, что никакой из данных векторов не может быть представлен как линейная комбинация других векторов. Такое свойство позволяет нам использовать орт векторы для построения базиса векторного пространства и решения систем линейных уравнений.

Важно понимать, что свойства орт вектора могут быть использованы в сочетании с другими математическими операциями и свойствами векторов для решения различных задач и проблем. Орт векторы – это мощный инструмент, который помогает нам визуализировать и анализировать сложные физические и математические явления.

Применение орт вектора

Графика и компьютерные игры

Орт векторы широко используются в области графики и компьютерных игр для определения направления и освещения объектов. Они позволяют задавать ориентацию камеры, расположение источников света и другие аспекты визуализации. Благодаря использованию орт векторов, создаются реалистичные и убедительные графические сцены, которые погружают игрока в виртуальный мир.

Робототехника и автономные системы

Орт векторы находят свое применение в области робототехники и автономных систем. Они используются для определения ориентации робота в пространстве, позволяя ему точно перемещаться и выполнять различные задачи. Орт векторы помогают роботам ориентироваться в окружающей среде и взаимодействовать с ней, делая их более умными и эффективными в работе.

Физика и инженерия

В физике и инженерии орт векторы используются для решения различных задач, связанных с механикой и электромагнетизмом. Они помогают определить направления силы, момента и других физических величин, а также учитывать ориентацию объектов при проектировании космических аппаратов, самолетов и других сложных систем. Орт векторы играют важную роль в анализе и моделировании различных физических явлений.

Навигация и география

В навигации и географии орт векторы используются для определения направления движения и местоположения объектов на поверхности Земли. Они помогают разработать системы GPS (глобального позиционирования), картографические приборы и другие средства ориентации. Орт векторы позволяют точно определить координаты объектов и направление движения, облегчая путешествия и обеспечивая безопасность в пути.

Медицина и биология

В медицине и биологии орт векторы находят применение для определения направления и ориентации внутри тела человека или живого организма. Они помогают в разработке методов исследования, определения патологий и планирования хирургических вмешательств. Орт векторы используются в медицинской томографии, рентгенологии и других методах диагностики, позволяя точно определить положение и размеры органов или опухолей.

В заключении, орт векторы имеют широкое применение в различных областях, от графики и компьютерных игр до медицины и биологии. Они позволяют определить направление и ориентацию объектов, улучшая качество визуализации, точность перемещения и понимание физических явлений. Изучение и применение орт векторов позволяют нам лучше понять и взаимодействовать с окружающим миром.

Способы построения орт вектора

1. Нормализация вектора

Один из самых простых способов построения орт вектора — это нормализация вектора. Для этого нужно разделить каждую компоненту вектора на его длину. Например, если у нас есть вектор v = (3, 4), то его длина равна √(3^2 + 4^2) = 5. Для получения орт вектора нужно разделить каждую компоненту на 5: (3/5, 4/5). Полученный вектор имеет длину 1 и является орт вектором.

2. Использование геометрических методов

Другой способ построения орт вектора — это использование геометрических методов. Например, если у нас есть вектор v = (3, 4), то его ортогональный вектор будет иметь координаты (4, -3). Это можно понять, если представить векторы геометрически: вектор (3, 4) будет направлен вправо и вверх, а его ортогональный вектор (4, -3) — вправо и вниз.

3. Использование матриц

Матрицы также могут быть использованы для построения орт вектора. Для этого нужно создать матрицу, в которой каждая строка или столбец соответствует каждой компоненте вектора, а длина вектора равна 1. Например, для вектора v = (3, 4) можно создать матрицу [3/5, 4/5]. Эта матрица является орт вектором.

Это только несколько способов построения орт вектора. В зависимости от конкретной задачи может быть использован иной подход. Однако, независимо от способа, орт вектор является важным инструментом для работы с векторами и может быть применен во многих областях.

Орт вектор: определение, свойства и применение

Свойства орт вектора:

• Длина орт вектора равна единице (|a| = 1).
• Орт вектор может быть упорядоченным (направленным) или неупорядоченным (беспорядочным).
• Два орт вектора, которые направлены в противоположных направлениях, называются сопряженными (a и -a).
• Скалярное произведение двух орт векторов равно нулю (a · b = 0).
• Орт векторы образуют ортогональную систему векторов.

Применение орт вектора:

1. Орт векторы используются для описания ориентации объектов в трехмерном пространстве, например, в компьютерной графике и 3D моделировании.
2. Орт векторы также используются в физике для моделирования и описания направления сил и моментов вращения.
3. В алгоритмах и методах обработки изображений и компьютерного зрения орт векторы используются для определения направления осей, контуров и границ объектов.