Орта в физике: понятие и применение

Физика — это наука о законах и явлениях природы, которая изучает свойства материи и ее взаимодействие с энергией. Орто (от греческого «ορθός» — прямой, правильный) — это термин, используемый в физике для описания объекта или явления, которое имеет определенную ориентацию или направление. Это понятие широко применяется в различных областях физики, таких как оптика, электродинамика, механика и др. Орто может быть применен для анализа или предсказания поведения объектов и взаимодействий между ними. С пониманием концепции орто в физике мы можем лучше понять и объяснить различные явления, происходящие в окружающем нас мире.

Определение и особенности орты

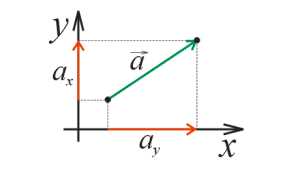
Как вы, наверное, уже догадались, орты – это оси или направления, которые можно использовать для описания положения или движения объектов в пространстве. Любую точку можно задать с помощью трех значений, соответствующих проекциям этой точки на оси. Оси, в свою очередь, перпендикулярны друг другу и образуют систему координат.

Каждая ось в трехмерном пространстве представляется вектором, который называется ортом. Орты обозначаются буквами i, j и k. Орт i соответствует оси x, орт j — оси y, а орт k — оси z. Орты i, j и k являются единичными векторами, что означает, что их длины равны 1.

Орты имеют важное свойство — они ортогональны друг другу. Это означает, что они перпендикулярны и образуют прямые углы между собой. Именно эта ортогональность делает орты полезными для описания различных физических явлений. Например, вектор скорости может быть разложен на проекции вдоль осей, используя орты, что позволяет более точно определить его направление и величину.

Орты также используются для описания углов, направлений, вращений и векторных величин в физике. Они играют ключевую роль в геометрии и линейной алгебре, а также во многих других областях науки и техники.

Определение орты

Когда мы говорим орт, можно представить себе стрелку, которая указывает определенное направление, как стрелки на компасе или указатель на дорожном знаке. Орты помогают нам ориентироваться и определить, куда направлен вектор.

Основные орты в трехмерном пространстве — это орт X, орт Y и орт Z. Орт X указывает вправо, орт Y указывает вверх, а орт Z указывает вперед. Эти орты образуют правую тройку ортогональных векторов, которые используются в системе координат, называемой декартовой системой координат. Координаты точек в трехмерном пространстве представляются векторами, состоящими из скалярных значений, умноженных на соответствующие орты.

Орты имеют длину единица и всегда перпендикулярны друг к другу. Они играют важную роль в различных областях физики, включая механику, электродинамику и оптику. Например, при рассмотрении движения тела или расчете электрического поля, орты позволяют определить направление и величину векторов, что в свою очередь помогает нам понять и предсказать различные явления и явления природы.

Понимание ортов является важной основой в физике и помогает нам добиться более глубокого понимания законов и принципов, которыми руководится природа. Без ортов было бы гораздо сложнее описывать и анализировать физические явления и решать различные задачи. Поэтому, понимание ортов и их применение являются ключевыми элементами в изучении и применении физики.

Особенности орты

1. Орты в пространстве

В трехмерном пространстве у нас есть три орта, которые образуют декартову систему координат — орт X, орт Y и орт Z. Они направлены вдоль осей координат и помогают нам ориентироваться в пространстве.

Например, представьте себе, что вы стоите на перекрестке двух улиц и вам нужно добраться до точки B, которая находится на улице, пересекающейся с вашей. Вы можете использовать орт X для движения вдоль своей улицы, а затем орт Y, чтобы перейти на другую улицу и добраться до точки B. Орты помогают нам описывать и перемещаться в пространстве.

2. Орты в электромагнетизме

Орты также широко используются в электромагнетизме, где мы имеем орты, определяющие направление магнитного поля и электрического поля.

Например, если у нас есть магнитное поле, направленное вверх, мы можем использовать орт Y для его описания. Если электрическое поле направлено вправо, мы можем использовать орт X. Орты в электромагнетизме помогают нам анализировать и решать различные электрические и магнитные задачи.

3. Орты в механике

В механике орты используются для описания и решения задач, связанных с движением тел и силами, действующими на них.

Например, при рассмотрении движения по плоскости мы можем использовать орт X и орт Y для описания перемещения объекта. Если на объект действует сила, мы можем использовать орт, направленный вдоль этой силы, чтобы анализировать его влияние на движение объекта. Орты помогают нам понять и решить механические задачи.

4. Орты в векторных операциях

Орты также используются при выполнении векторных операций, таких как умножение вектора на скаляр или нахождение скалярного или векторного произведения двух векторов.

Например, при умножении вектора на скаляр, мы умножаем каждую компоненту вектора на этот скаляр. Орты помогают нам определить направление и значению каждой компоненты исходного вектора. Орты играют ключевую роль в векторных операциях и облегчают выполнение различных вычислений.

В итоге, орты — это неотъемлемая часть физики, которая помогает нам лучше понимать и анализировать различные физические явления. Они позволяют нам описывать и перемещаться в пространстве, а также решать задачи, связанные с электромагнетизмом и механикой. Орты являются мощным инструментом, который позволяет нам углубить наше понимание физических законов и явлений.

Применение орт в физике

Один из основных способов применения орт — это описание направлений и ориентаций. Например, в векторном анализе, орты используются для определения направления векторов. Допустим, мы имеем вектор силы, который действует на тело. С помощью ортов мы можем определить направление этой силы и тем самым узнать, куда она направлена.

Орты также играют важную роль при решении задач, связанных с расчетами векторных произведений и скалярных произведений. Векторное произведение двух векторов дает новый вектор, который перпендикулярен плоскости, образованной исходными векторами. Орт этой плоскости определяется с помощью ортов исходных векторов. Скалярное произведение двух векторов, с другой стороны, можно выразить через косинус угла между ними, что также требует знания ортов.

В некоторых случаях, орты также обозначают различные координатные оси. Например, в трехмерном пространстве, орты x, y и z обычно используются для обозначения осей, соответствующих координатам x, y и z. Это позволяет нам описывать положение точек в пространстве с помощью координат и ортов.

Кроме того, орты также применяются в оптике и электромагнетизме. Например, они используются для описания поляризации света и различных волн электромагнитного излучения. Орты помогают определить направление колебаний электрического и магнитного полей в этих явлениях.

Математическое использование орт

Математический подход к использованию орта существенно облегчает анализ сложных физических явлений и решение различных задач. Например, при описании движения объекта может потребоваться знание его скорости и направления. Для этого используется векторная алгебра, где орты служат базисными векторами, описывающими координатные оси.

Орты обладают свойством ортогональности, что означает, что они перпендикулярны друг другу. Это свойство позволяет нам удобно работать с векторами и проводить анализ сил, давления, электрических полей и других физических величин.

Математическое использование орта в физике позволяет нам решать различные задачи, такие как вычисление работы, мощности, ускорения и других физических величин. Оно также позволяет нам описывать и анализировать сложные физические системы, такие как электрические цепи, механические динамические системы и другие.

Использование орта в физике является неотъемлемой частью нашего понимания и исследования окружающего нас мира. Благодаря этому инструменту мы можем более точно описывать физические процессы и предсказывать их последствия. Поэтому понимание и использование орта значительно облегчает наше изучение физики и применение ее в реальной жизни.

Применение орт в векторной алгебре

Орты широко используются во многих областях физики, таких как механика, электромагнетизм, оптика и др. Например, в механике они помогают описывать движение и силы. Вектор скорости, ускорения и силы могут быть разложены на компоненты при помощи ортов, что значительно облегчает их анализ и вычисления.

Орты также применяются в электромагнетизме для описания электрических и магнитных полей. Направление векторов электрического поля и магнитной индукции может быть выражено с использованием ортов. Это позволяет адекватно описывать и понимать поведение электромагнитных волн и сил в пространстве.

Кроме того, орты применяются в оптике для описания поляризации света. Поляризация – это особенность световой волны, выражающая направление колебаний электрического поля в пространстве. Орты используются для описания осей поляризации и визуального представления направления светового вектора.

Применение ортов в векторной алгебре позволяет более удобно и точно описывать физические явления и процессы в пространстве. Это помогает упростить расчеты, предсказать результаты экспериментов и развивать новые методы и модели в физике. Орты являются важным инструментом для работы с векторами и играют важную роль в различных областях физики.

Орта в физике: понятие и применение

Орт может быть полезен для определения направлений, углов, взаимоотношений и геометрических свойств объектов. Его концепция применяется во множестве физических дисциплин, включая механику, электромагнетизм, оптику, квантовую механику и другие.

Примеры применения орта в физике:

• Орты вектора: Вектор может быть разложен на ортогональные компоненты, которые обозначаются как единичные векторы. Эти единичные векторы являются ортами, которые показывают направление и ортогональность вектора.
• Ортонормированные базисы: В некоторых случаях, векторы могут быть выбраны так, чтобы образовать ортонормированный базис. Это означает, что все векторы являются ортогональными друг к другу и имеют единичную длину.
• Операторы ортогональности: В математике и физике используются операторы ортогональности, которые проецируют векторы на ортогональные подпространства или выполняют ортогонализацию векторов. Это позволяет упростить вычисления и решение уравнений.
• Орты функций: В квантовой механике, функции могут быть описаны с использованием ортонормированных базисных функций, таких как функции собственных значений операторов. Операторы выбираются так, чтобы они имели ортогональные или перпендикулярные собственные функции.

Использование орта в физике позволяет упростить анализ объектов и величин, а также установить взаимоотношения и свойства между ними. Он является важным инструментом для понимания и объяснения физических явлений и процессов.