Ортоцентр треугольника: определение и основные свойства

Ортоцентр – это одна из ключевых точек в геометрии треугольника, которая привлекает внимание своей уникальностью. Итак, что же такое ортоцентр и какие свойства ему присущи? Ортоцентр – это точка пересечения высот треугольника, или, другими словами, точка, в которой проходят все перпендикуляры, опущенные из вершин треугольника на прямые, содержащие стороны, противоположные этим вершинам. Каждый треугольник имеет свой собственный ортоцентр, и его местоположение может меняться в зависимости от формы треугольника. Погрузимся глубже в изучение этой интересной и полезной точки, и узнаем больше о ее свойствах и особенностях.

Определение ортоцентра

Для определения ортоцентра треугольника, следует построить высоты из каждой вершины треугольника и найти точку их пересечения.

Во-первых, построим высоту AE из вершины A. В результате получим перпендикуляр, опущенный из вершины A на сторону BC.

Затем нарисуем высоту BD из вершины B. Получим перпендикуляр, опущенный из вершины B на сторону AC.

Наконец, построим высоту CF из вершины C. Получим перпендикуляр, опущенный из вершины C на сторону AB.

Ортоцентром и будет точка пересечения высот треугольника.

Ортоцентр имеет несколько интересных свойств. Например, суммы углов, образованных ортоцентром с вершинами треугольника, равны 180 градусов. Это означает, что ортоцентр находится на окружности, проходящей через вершины треугольника и его центральную точку — окружность Эйлера.

Ортоцентр также является центром подобия для треугольников, образованных вершинами и серединными точками сторон исходного треугольника. Это значит, что при подходящей масштабировании и повороте, ортоцентр остается неподвижным.

Ортоцентр — важная точка в геометрии и имеет множество интересных и полезных свойств. Построение ортоцентра и изучение его свойств помогают нам лучше понять геометрические особенности треугольника и его взаимосвязи с другими фигурами.

Существование ортоцентра

Чтобы понять, существует ли ортоцентр в данном треугольнике, нужно взглянуть на его углы. Окей, мне интересно, а что, если все углы прямые? Тогда существование ортоцентра становится спорным. Но не волнуйтесь, в реальном мире такое случается редко.

Вопрос: А что, если все углы треугольника тупые? Может ли быть ортоцентр в таком случае?

Ответ прост: нет, ортоцентра в таком треугольнике быть не может. Ведь ортоцентр — это точка пересечения высот треугольника, а высоты проходят через вершины и перпендикулярны к противолежащим сторонам. В тупоугольном треугольнике высоты лежат за пределами треугольника.

Очень интересно, не правда ли? Ортоцентр — это нечто особенное в треугольнике, кто-то, кто связывает все его углы и стороны. Он добавляет глубину и гармонию, и важно помнить, что он существует не всегда. Так что, следующий раз, когда вы встретите треугольник, подумайте о его ортоцентре и увидьте красоту и симметрию, которые он приносит в этот мир геометрии!

Способы определения ортоцентра

1. Построение высот

Первый способ – это построение высот треугольника. Высота – это линия, которая проходит через вершину треугольника и перпендикулярна противоположной стороне. Существуют различные методы построения высот треугольника, включая использование циркуля и линейки или теоремы о прямоугольных треугольниках.

Когда вы построили все три высоты треугольника, их пересечение является ортоцентром.

2. Теорема о перпендикулярных биссектрисах

Второй способ основан на теореме о перпендикулярных биссектрисах треугольника. Биссектриса – это линия, которая делит угол треугольника на две равные части. Если построить биссектрисы для каждого угла треугольника, они будут перпендикулярны друг к другу в точке, называемой центром биссектрис.

Ортоцентр треугольника является центром биссектрис и пересечением перпендикулярных биссектрис.

3. Прямоугольный треугольник

Третий способ основан на знании, что ортоцентр треугольника является центром окружности, описываемой около прямоугольного треугольника, то есть треугольника, у которого один из углов является прямым. Для определения ортоцентра в этом случае нужно найти середины сторон треугольника и провести линии, соединяющие середины сторон с противоположными вершинами. Они пересекутся в ортоцентре.

Итак, теперь вы знаете несколько способов определить ортоцентр треугольника. Приступайте к решению задач о треугольниках с уверенностью и не забывайте практиковаться!

Основные свойства ортоцентра

1. Высоты пересекаются в ортоцентре

Первое и наиболее примечательное свойство ортоцентра заключается в том, что все высоты треугольника пересекаются именно в этой точке. Это означает, что если мы проведем высоты из каждой вершины треугольника, то они все пересекутся в одной точке — ортоцентре.

2. Сумма углов при вершинах равна 180 градусам

Другое интересное свойство ортоцентра связано с углами треугольника. Если мы посмотрим на углы, образованные сторонами треугольника и линиями, соединяющими вершины с ортоцентром, то заметим, что их сумма всегда равна 180 градусам. То есть, если мы сложим углы при вершинах треугольника и углы между сторонами и линиями, идущими к ортоцентру, то получим 180 градусов.

3. Ортоцентр лежит внутри, на сторонах или вовсе снаружи треугольника

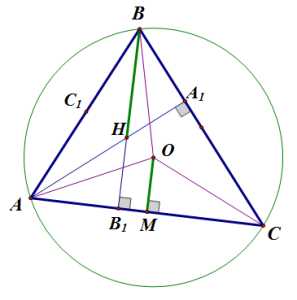
Ортоцентр может находиться как внутри треугольника, так и на его сторонах, и даже вовсе снаружи. Это зависит от особенностей треугольника. Например, если все углы треугольника острые, то ортоцентр будет внутри треугольника. Если же один из углов острый, а два других тупые, то ортоцентр будет лежать на сторонах треугольника. Если все углы тупые, то ортоцентр будет снаружи треугольника.

4. Отношение расстояний от ортоцентра до вершин треугольника

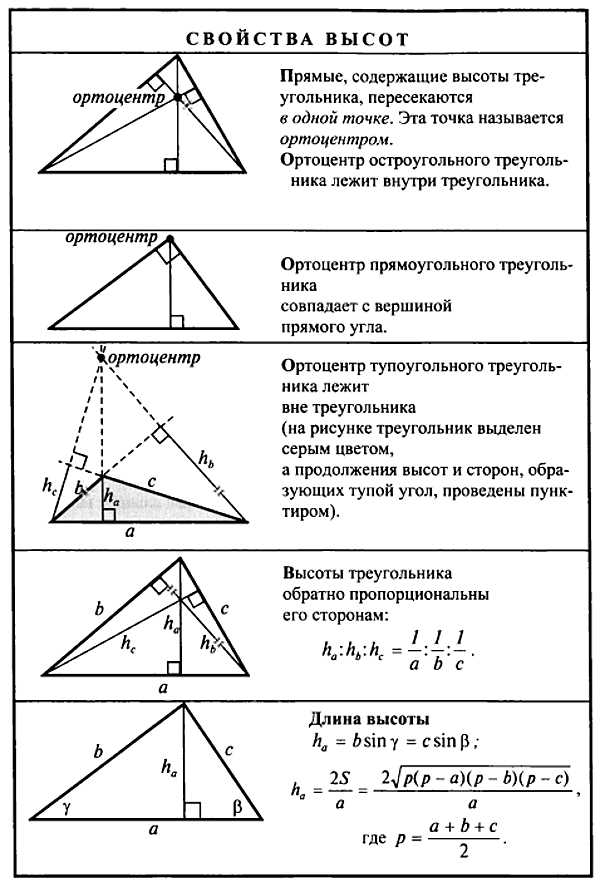
Известно также, что отношение расстояния от ортоцентра до вершины треугольника к расстоянию от ортоцентра до середины соответствующей противоположной стороны равно 2:1. Это интересное свойство демонстрирует определенную геометрическую закономерность и может быть использовано для решения задач, связанных с ортоцентром и треугольником.

Все эти основные свойства ортоцентра делают его уникальным и важным элементом треугольника. Он является ключевой точкой, связанной с высотами, углами и расстояниями в треугольнике. Познакомиться и изучить эти свойства поможет лучше понять и анализировать геометрические проблемы и задачи, связанные с ортоцентром и треугольником.

Ортоцентр и основные элементы треугольника

Ортоцентр треугольника имеет свойства, которые стоит знать. Во-первых, ортоцентр лежит внутри треугольника, или на его сторонах, или на его продолжении. Во-вторых, сумма расстояний от ортоцентра до всех вершин треугольника равна нулю. В-третьих, ортоцентр треугольника является вершиной описанного вокруг треугольника окружности, вписанного в треугольник окружности и описанного окружности правильного равносторонного треугольника.

Почему ортоцентр так важен? Он играет ключевую роль во многих свойствах и задачах, связанных с треугольниками. Например, ортоцентр лежит на прямой, проведенной через середины сторон треугольника (средняя линия). Также ортоцентр является центром окружности Эйлера — окружности, проходящей через основания высот треугольника.

Теперь давайте представим себе треугольник и рассмотрим основные элементы, связанные с ортоцентром. Представьте каждую из трех сторон треугольника как отрезок между двумя его вершинами. Тогда каждая сторона треугольника имеет свою медиану, которая является отрезком, соединяющим середину стороны с противоположной вершиной. В медиане точно в середине лежит точка, называемая серединой медианы.

Интересно, что середины медиан треугольника лежат на одной прямой и эта прямая проходит через ортоцентр треугольника. Невероятно, не правда ли? Однако это факт! Это свойство является одним из многих удивительных свойств, связанных с ортоцентром и основными элементами треугольника.

Как видите, ортоцентр и основные элементы треугольника тесно связаны друг с другом, и изучение их свойств может помочь нам лучше понять геометрию треугольников, их связи и основные закономерности. Используя эти знания, мы сможем решать сложные задачи, проводить доказательства и расширять свой кругозор.

Отношение расстояний до ортоцентра

Давайте сразу взглянем на интересующий нас треугольник. Вот он, с его вершинами A, B и C:

• Вершина A имеет координаты (x₁, y₁);
• Вершина B имеет координаты (x₂, y₂);
• Вершина C имеет координаты (x₃, y₃).

Теперь нам нужно найти координаты ортоцентра. Это можно сделать, найдя перпендикуляры к сторонам треугольника, проходящие через середины этих сторон. Мы получим три точки пересечения этих перпендикуляров, и среди них будет ортоцентр.

После нахождения координат ортоцентра, мы можем рассчитать расстояние от каждой вершины до этой точки. Для этого используйте простую формулу расстояния между двумя точками: √((x₂ — x₁)² + (y₂ — y₁)²).

Теперь, чтобы найти отношение расстояний от вершин треугольника до ортоцентра, разделим расстояние от каждой вершины до ортоцентра на отношение суммы двух других расстояний от вершин к ортоцентру.

Обозначим расстояние от вершины A до ортоцентра H как D_AH, от вершины B до ортоцентра H как D_BH, и от вершины C до ортоцентра H как D_CH.

Таким образом, получаем формулу для отношения расстояний: (D_AH / (D_BH + D_CH)), (D_BH / (D_AH + D_CH)), (D_CH / (D_AH + D_BH)).

Теперь, если мы подставим значения расстояний в формулу, мы получим искомый результат. Отношение расстояний до ортоцентра помогает нам понять, какую долю каждая вершина треугольника занимает от общего расстояния до ортоцентра.

Это очень интересное свойство, которое можно использовать при изучении треугольников и решении задач, связанных с ортоцентром. Надеюсь, вы сами сможете проверить это свойство на практике и убедитесь в его правильности.

Ортоцентр треугольника: определение и основные свойства

Высотами треугольника называются отрезки, проведенные из вершины треугольника к противоположным сторонам и перпендикулярные этим сторонам. Они образуют треугольник, который называется высотником.

Основные свойства ортоцентра треугольника:

• Ортоцентр лежит внутри, на сторонах или на продолжениях сторон треугольника, в зависимости от типа треугольника.
• Ортоцентр треугольника является центром описанной окружности высотником.
• Ортоцентр является точкой пересечения медиан треугольника, которые также проходят через центр тяжести треугольника.
• Углы треугольника, образованные сторонами и высотами, являются прямыми.

Ортоцентр треугольника играет важную роль в геометрии и имеет множество свойств и применений в различных задачах и теоремах.