Ось координат и координаты точки – это одни из основных понятий в математике, которые широко применяются в различных областях науки, техники и ежедневной жизни. Ось координат представляет собой прямую линию, разделенную на две половины, каждая из которых имеет свою направленность и указывает на положение точки относительно начала отсчета. Координаты точки – это числа, которые определяют положение точки на оси координат. Используя ось координат и координаты точки, мы можем решать задачи по определению расстояния, направления, перемещения и других важных параметров. В этой статье мы рассмотрим более подробно понятие оси координат и координат точки, а также рассмотрим их применение на примерах из жизни.
Ось координат
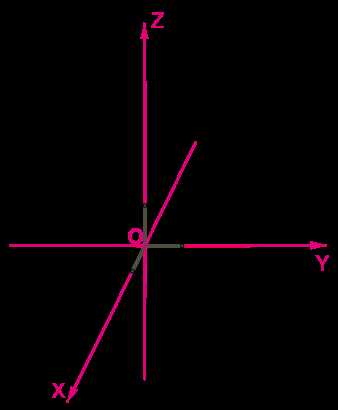
Начало координат обозначается буквой O и служит как опорная точка для измерения расстояний. Вертикальная линия называется осью Y, а горизонтальная — осью X. Пользуясь этими осями, мы можем определить положение точки на плоскости.
Каждая точка на оси координат имеет свои координаты, которые показывают насколько она удалена от начала координат по каждой оси. Например, точка (3, 4) означает, что она находится на 3 единицы вправо от начала координат и на 4 единицы вверх.
Ось координат является важным инструментом в математике и физике. Она позволяет нам описывать и анализировать различные явления и отношения между объектами. Все виды графиков и диаграмм используют ось координат для отображения данных и понимания зависимости между переменными.
Например, ось координат может использоваться для решения задачи, связанной с движением объекта. Если мы знаем начальное положение объекта и его скорость, ось координат позволяет нам определить, где объект будет находиться в определенный момент времени.
Также ось координат может использоваться для построения графиков функций. График функции — это графическое представление зависимости между входными и выходными значениями функции. Ось X представляет входные значения, а ось Y — выходные значения. С помощью графика функции мы можем анализировать ее поведение и находить решения уравнений и неравенств.
Таким образом, ось координат играет важную роль в различных областях науки и позволяет нам лучше понять и описать мир вокруг нас. Используйте ее на практике и задавайтесь вопросами: какие точки находятся на определенном расстоянии от начала координат? Как можно описать движение объекта с помощью оси координат? Какие данные можно представить на графике функции?
Определение оси координат

Представьте, что вы находитесь в центре большой комнаты и к вашему мнению первую ось координат всегда зрительная. Комната имеет две стены, и вы решаете назвать одну стену «горизонтальной осью» и другую стену «вертикальной осью». Теперь вы можете указать местоположение любой точки в комнате, используя эти две оси.
Точно так же и в математике оси координат представляют собой систему двух перпендикулярных линий, которые пересекаются в одной точке, называемой началом координат. Одна линия называется горизонтальной осью, а другая — вертикальной осью. Где они пересекаются, устанавливается начало координат, обозначаемое точкой O.
Горизонтальная ось обычно обозначается буквой X, а вертикальная ось — буквой Y. Таким образом, каждая точка в двумерной плоскости может быть указана с помощью двух чисел, обозначающих ее положение по горизонтальной и вертикальной осям.
Ось X расположена горизонтально слева направо от начала координат, а ось Y расположена вертикально снизу вверх. Положительные значения на оси X находятся справа от начала координат, а отрицательные значения — слева. По аналогии, положительные значения на оси Y находятся выше начала координат, а отрицательные значения — ниже.
Обратите внимание, что оси координат являются бесконечными, расширяясь во всех направлениях. Таким образом, мы можем указать положение любой точки в плоскости с помощью ее координат X и Y.
Итак, ось координат — это система двух перпендикулярных линий, которые помогают нам определить положение любой точки на плоскости. Они играют важную роль в математике, физике, графиках и многих других областях, где точное описание положения точек является неотъемлемой частью работы.
Прямая система координат
Каждая точка на плоскости может быть определена с помощью двух чисел, называемых координатами. Первое число соответствует расстоянию от точки до вертикальной оси Y и называется ординатой или Y-координатой. Второе число соответствует расстоянию от точки до горизонтальной оси X и называется абсциссой или X-координатой.
Прямая система координат применяется во многих областях, включая физику, геометрию, экономику, программирование и графический дизайн. Она позволяет нам анализировать и визуализировать данные, строить графики функций, решать уравнения и многое другое.
Представим, что ты оказался в центре координатной плоскости и хочешь узнать свое положение. Ты можешь определить свои координаты, измерив расстояние до горизонтальной и вертикальной осей. Если ты находишься, например, 3 единицы вправо от начала координат и 2 единицы вверх, твои координаты будут (3,2).
Кроме того, прямая система координат может быть использована для определения расстояния между двумя точками. Для этого мы используем теорему Пифагора. Если у нас есть точки A и B с координатами (x1, y1) и (x2, y2) соответственно, то расстояние между ними можно найти по формуле: √((x2-x1)^2 + (y2-y1)^2).
Прямая система координат может быть представлена в виде таблицы с двумя столбцами: один столбец для значений X-координаты, а другой — для значений Y-координаты. Такая таблица помогает держать трек своей позиции на плоскости и строить графики функций.
Плоская система координат
Определим плоскую систему координат более подробно. Начнем с оси абсцисс — это горизонтальная ось, которая обозначается буквой «x». Ось абсцисс разделяет плоскость на две части — положительную и отрицательную. Ноль на оси абсцисс обозначается точкой, которая называется началом координат.
Теперь обратим внимание на ось ординат — это вертикальная ось, которая обозначается буквой «y». Ось ординат также разделяет плоскость на положительную и отрицательную части. Ноль на оси ординат располагается в точке, пересечении с осью абсцисс, образуя начало координат.
Таким образом, плоская система координат представляет собой двумерное пространство, в котором каждая точка имеет две координаты — абсциссу и ординату. Абсцисса определяет положение точки по горизонтальной оси, а ордината — по вертикальной.
Это очень полезный инструмент, который нашел свое применение в различных областях, таких как математика, физика, экономика и даже в повседневной жизни. Он позволяет нам легко определить расстояние между точками, находить углы, строить графики функций и многое другое.
Итак, плоская система координат — это мощный инструмент для определения точного положения объектов на плоскости. Она предоставляет нам возможность визуализировать и анализировать различные явления и явления, происходящие в двумерном пространстве. Используя этот инструмент, мы можем легко разбить и понять мир вокруг нас.
Координаты точки
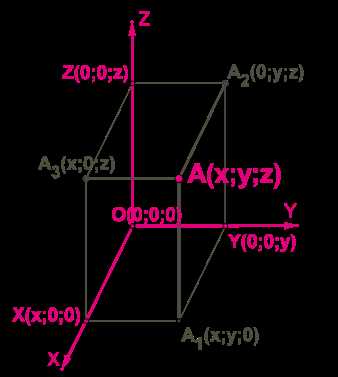
Координаты точки — это как бы ее адрес на плоскости. Чтобы указать положение точки, мы используем два числа, которые называются координатами. Первое число показывает разницу в расстоянии между точкой и вертикальной осью, а второе число показывает разницу в расстоянии между точкой и горизонтальной осью. Удобно, правда?
Координаты точки обычно записываются в виде упорядоченной пары чисел, разделенных запятой и заключенных в скобки. Например, (3, 4) — это координаты точки, которая находится 3 единицы от вертикальной оси и 4 единицы от горизонтальной оси.
Если вы когда-то играли в игру «Морской бой», то, скорее всего, вы уже знаете, как использовать координаты точки. Вы должны были указать координаты, чтобы «стрелять» в определенные ячейки и попытаться потопить корабли противника.
Координаты точек также используются в географии для определения местоположения городов, стран и других географических объектов. Они также важны в физике, чтобы описать движение объектов в пространстве и время.
Так вот, теперь у вас есть представление о том, что такое координаты точки. Они помогают нам определить местоположение точки на плоскости и используются в различных областях науки и техники. В следующий раз, когда вы играете в игры или интересуетесь географией, подумайте о том, какие координаты скрыты за этими предметами и местами. И возможно, с помощью знания координат, вы сможете открыть для себя что-то новое и захватывающее!
Определение координат точки
Для удобства измерения и записи положения точки на плоскости, система координат была введена. Оси координат — это две перпендикулярные прямые, на которых значения координат точки отмечаются. Ось, идущая слева направо, называется горизонтальной осью или осью x, а ось, идущая сверху вниз, называется вертикальной осью или осью y.
Каждая из осей имеет свое начало, которое обозначается точкой с координатами (0,0). Это начало называется началом координат или точкой пересечения осей.
Чтобы задать конкретные координаты точки, сначала нужно определить, находится ли она выше или ниже вертикальной оси, а затем левее или правее горизонтальной оси. Далее, отсчитывая значения по каждой оси, мы можем определить точные числовые значения координат точки.
Например, если точка находится выше оси x и левее оси y, ее координаты будут отрицательными. Если же она находится ниже оси x и правее оси y, ее координаты будут положительными.
Знание координат точки позволяет нам точно определить ее положение на плоскости, а также выполнять различные действия, такие как нахождение расстояния между точками и построение графиков функций.
Ось координат и координаты точки: понятие и применение
Координаты точки — это числа, которые указывают расстояние от точки до начала координатных осей. Координаты точки на оси абсцисс обозначаются числом x, а на оси ординат — числом y. Точка с координатами (0, 0) называется началом координат или точкой пересечения координатных осей.
Координаты точки могут быть положительными или отрицательными, в зависимости от ее положения относительно начала координат. Если точка находится выше оси абсцисс, то координата y будет положительной. Если точка находится ниже оси абсцисс, то координата y будет отрицательной. Если точка находится правее оси ординат, то координата x будет положительной. Если точка находится левее оси ординат, то координата x будет отрицательной.
Одним из основных применений оси координат и координат точек является построение графиков функций и изображение геометрических фигур. С их помощью можно анализировать различные параметры функций и фигур, определять их свойства и решать задачи связанные с расстояниями, площадями и другими характеристиками.