Ось тангенса: определение
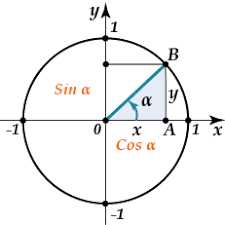
Для понимания оси тангенса нужно знать, что тангенс угла определяется как отношение противолежащей стороны к прилежащей стороне. Например, если у нас есть прямоугольный треугольник со сторонами a и b, угол между сторонами a и гипотенузой отмечен как θ, то тангенс угла θ будет равен отношению a к b.
Ось тангенса представлена на графике с измерениями в углах, как правило, в радианах. Каждое значение угла соответствует определенному значению на оси тангенса. Таким образом, ось тангенса является инструментом для визуализации и анализа зависимостей между углами и значениями тангенса.
Ось тангенса имеет ряд основных свойств и характеристик. Например, она имеет периодичность равную π (или 180 градусам) и является неограниченной в обеих направлениях. Это означает, что для каждого угла существует бесконечное количество значений на оси тангенса.
Ось тангенса широко используется в различных областях, включая физику, инженерию, компьютерную графику и др. Она позволяет ученым и специалистам анализировать и предсказывать разные явления и их зависимости от углов и значений тангенса.
Таким образом, ось тангенса – это инструмент, который помогает нам лучше понять и визуализировать значения тангенса для различных углов, и может быть полезным при решении разных математических и физических задач. Попробуйте использовать ось тангенса в своих расчетах и исследованиях и увидите, как она может помочь вам лучше понять и объяснить различные феномены и процессы.
Что такое ось тангенса?
Ось тангенса играет важную роль в математике, особенно в тригонометрии. Она позволяет нам определить функцию тангенс и исследовать его свойства.
Но что такое тангенс и зачем нам это нужно? Вот пример, чтобы прояснить. Представь, что ты планируешь поход в горы. Любая гора имеет свою высоту и уклон, и ты хочешь знать, какой уклон надо преодолевать, чтобы достичь вершины. Вот в таких случаях и пригодится функция тангенс.
Функция тангенс равна отношению противолежащего катета (высоты горы) к прилежащему катету (горизонтальное расстояние). Она показывает, насколько круто ты будешь подниматься в гору при движении вдоль почти вертикального угла.
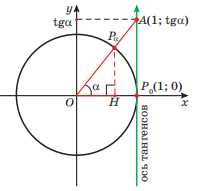
Ось тангенса позволяет нам измерить этот уклон. Если мы возьмем начало координат и будем двигаться вдоль оси тангенса, то получим все возможные значения тангенса.
Интересно, что ось тангенса проходит через все кратные числа пи (π). Значит, ось тангенса тесно связана с геометрией окружности и треугольниками.
Так что ось тангенса – это не просто линия на графике, а важный инструмент в изучении математических и геометрических концепций. Она помогает нам понять и применить тангенс, чтобы решать различные задачи, связанные с измерением углов и уклонов.
Свойства оси тангенса
1. Периодичность
Одно из главных свойств оси тангенса — ее периодичность. Функция тангенс имеет период равный π, это означает, что ее значения повторяются с постоянным интервалом каждые π радиан. Такая периодичность оси тангенса позволяет анализировать и предсказывать поведение функции на определенных интервалах.
Например, если мы знаем, что значение тангенса угла равно 1 на интервале от 0 до π/4, то мы можем с уверенностью сказать, что значение тангенса угла на интервале от π/4 до π/2 также будет равно 1.
2. Асимптоты
Ось тангенса имеет две асимптоты: горизонтальную и вертикальную. Горизонтальная асимптота задает границу для значений оси тангенса и равна ±∞. Это означает, что значения оси тангенса никогда не достигают бесконечности, но могут быть очень большими или очень малыми.
Вертикальная асимптота проходит через точки π/2 + πk, где k — целое число. Эта асимптота показывает, что ось тангенса имеет разрыв в этих точках и не существует значений функции в этих точках.
3. Симметричность
Ось тангенса обладает свойством симметричности относительно начала координат. Это означает, что значения функции в точках (-x, -y) и (x, y) симметричны относительно начала координат.
Например, если мы знаем, что тангенс угла α равен 2, то мы можем сказать, что тангенс угла -α также будет равен 2.
4. Монотонность
Ось тангенса является монотонной функцией на каждом из своих интервалов между вертикальными асимптотами. Это означает, что значения функции на каждом таком интервале будут либо все положительными, либо все отрицательными.
Например, на интервале (0, π/2) значения оси тангенса будут положительными, а на интервале (-π/2, 0) будут отрицательными.
5. Нули и экстремумы
Ось тангенса имеет нули, то есть значения функции, при которых тангенс равен нулю. Нули оси тангенса находятся в точках, где значения функции пересекают ось x.
Также ось тангенса имеет точки экстремума, в которых значения функции достигают максимума или минимума. Эти точки находятся вблизи вертикальных асимптот и равны ±∞.
Ось тангенса имеет множество свойств и особенностей, которые делают ее полезной и интересной для изучения. Она находит применение в физике, инженерии, компьютерных науках и других областях, где необходимо анализировать и моделировать зависимости и взаимодействия между величинами.
Свойства оси тангенса
1. Ограниченность. Ось тангенса имеет ограниченное множество значений. Ее значения находятся в промежутке от минус бесконечности до плюс бесконечности, и она периодическая с периодом равным pi (пи).
2. Асимптоты. У оси тангенса есть горизонтальные асимптоты. Они расположены на высоте целых кратных периода pi/2 (пи/2). То есть, если мы находимся на точке графика, у которой значение аргумента является pi/2 (пи/2), то тангенс этого аргумента равен плюс бесконечности. Аналогично, если значение аргумента равно 3pi/2 (3пи/2), то тангенс равен минус бесконечности.
3. Непрерывность. Ось тангенса является непрерывной функцией везде, кроме точек, где возникают вертикальные асимптоты. В таких точках, тангенс принимает значения плюс или минус бесконечность в зависимости от знака приближения к точке справа или слева.
4. Кривая стремится к асимптотам. Когда аргумент оси тангенса стремится к плюс или минус бесконечности, значение функции стремится к горизонтальным асимптотам. Это значит, что тангенс быстро увеличивается или уменьшается, когда значение аргумента увеличивается или уменьшается бесконечно.
5. Зеркальность. Ось тангенса симметрична относительно начала координат. Это значит, что значения функции находятся на одинаковом расстоянии от оси OX, но с противоположными знаками. Например, если тангенс аргумента равен 3, то тангенс аргумента с противоположным знаком, равен -3.
Это лишь некоторые из свойств оси тангенса, которые помогают нам понимать и использовать эту функцию в различных задачах. Зная их, мы можем более уверенно и эффективно работать с осью тангенса и извлекать пользу из ее свойств.
Применение
Одним из главных применений оси тангенса являются задачи на вычисление высот. Например, при измерении высоты горы или высоты здания можно использовать ось тангенса для определения угла наклона и подсчета необходимых данных. Благодаря этому, инженеры и строители могут точно рассчитать не только высоту объектов, но и подходящие материалы для строительства.
Ось тангенса также находит применение в геодезии. С помощью нее можно измерять расстояния между объектами, угол между ними и высоту горизонтальных плоскостей. Это важно для создания карт и планов, а также для выявления неровностей и предупреждения природных катастроф.
Кроме того, ось тангенса используется в физике. Например, при изучении движения тела под углом к горизонту можно рассчитать силу, скорость и траекторию тела с помощью оси тангенса. Это особенно важно в механике, аэродинамике и других дисциплинах, где изучается движение тел.
Кроме применения в науке и технике, ось тангенса находит свое применение и в повседневной жизни. Например, при построении и установке мебели, определении угла наклона наклонной поверхности или даже при решении головоломок и геометрических задач. Ось тангенса упрощает эти процессы и помогает нам решать задачи быстрее и точнее.
Итак, ось тангенса нашла широкое применение в науке, технике и повседневной жизни. Она помогает нам решать различные задачи, определять углы, высоты и расстояния. Используя ось тангенса, мы можем быть уверены в точности наших расчетов и решений. Без этого инструмента, многие задачи и проблемы были бы гораздо сложнее для нас. Поэтому, необходимо оценить и уважить применение оси тангенса в нашей жизни и использовать ее в полной мере.
Ось тангенса: определение, свойства, применение
Ось тангенса обладает рядом свойств, которые делают ее полезной в различных областях науки и техники:
- Симметрия: Ось тангенса является симметричной относительно оси ординат. Это означает, что значения тангенса для углов, лежащих по разные стороны от оси тангенса, будут отрицательными и будут иметь одинаковую абсолютную величину.
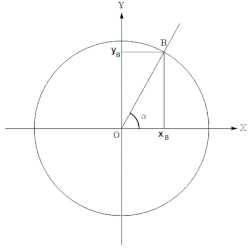
- Определение угла: Ось тангенса позволяет определить тангенс угла между отрезком, проведенным от начала координат до точки на графике, и положительным направлением оси абсцисс. Тангенс этого угла будет числовым значением, выражающим отношение длины отрезка к длине отрезка, проведенного по оси абсцисс от начала координат до точки пересечения отрезка с осью ординат.
Из-за своих свойств ось тангенса применяется во многих областях, включая физику, инженерию и математику. Например, в физике она используется для вычисления траекторий движения тела под углом к горизонту, а в инженерии — для определения угла наклона поверхностей и направления движения механизмов.