Знакомство с темами математического анализа может быть довольно запутанным, но понимание основных концепций поможет сделать их более доступными. В числовом выражении, указанным после основания, основание является числом, а показатель степени — это число, указанное над основанием и определяющее его степень. Например, в выражении 2^3 основание равно 2, а показатель степени равен 3. Знание основания и показателя степени позволяет нам выполнить операцию возведения в степень и определить результат этой операции. В данной статье мы рассмотрим, что такое основание и показатель степени и как правильно их использовать.
- Что такое основание и показатель степени?
- Основание степени: что это такое и как использовать?
- Показатель степени
- Как использовать основание и показатель степени?
- Основание степени
- Показатель степени
- Применение в практических задачах
- Операции с основаниями и показателями степеней
- Основание и показатель степени: что это такое и как использовать?
Что такое основание и показатель степени?
Основание – это число, которое умножается само на себя определенное количество раз. Например, в выражении 2^3, число 2 является основанием, потому что оно умножается на само себя три раза: 2 * 2 * 2 = 8. Основание может быть любым числом, положительным или отрицательным.
Показатель степени – это число, указывающее, сколько раз нужно умножить основание на само себя. В примере выше, число 3 является показателем степени, потому что основание 2 умножается на само себя три раза. Показатель степени также может быть любым числом, положительным или отрицательным.
Основание и показатель степени вместе образуют выражение, которое часто называется степенным числом. Например, в выражении 2^3, число 2 является основанием, а число 3 – показателем степени. Вместе они образуют степенное число 8.
Зачем нам нужно использовать основание и показатель степени? Они позволяют нам упростить сложные выражения и работать с числами больших порядков. Например, вместо того чтобы записывать число 2, как произведение самого себя много раз (2 * 2 * 2 * …), мы можем записать его в виде степенного числа 2^3. Это упрощает запись и позволяет нам легко выполнять различные операции, такие как умножение и деление степенных чисел.
Теперь, когда мы знаем, что такое основание и показатель степени, мы можем использовать их в наших вычислениях и задачах. Они помогают нам понять и упростить сложные математические операции и представить числа в более компактной форме. Попробуйте применить эти понятия в практике и увидите, как они могут упростить вашу работу с числами!
Основание степени: что это такое и как использовать?
Для лучшего понимания, давайте рассмотрим пример. Предположим, у нас есть число 2 и мы хотим возвести его в степень 3. Это означает, что мы умножаем число 2 на себя три раза: 2 * 2 * 2 = 8. В этом примере число 2 является основанием, а число 3 – его степенью.
Основание степени важно, так как оно определяет результат и характер степени. Поэтому важно выбирать правильное основание, чтобы получить желаемый результат. Например, если мы хотим найти квадрат числа 5, основание степени будет 5, а показатель степени будет 2. Таким образом, 5^2 = 25.
Когда мы используем основание степени, мы можем получить различные результаты, в зависимости от того, какое число мы выбираем в качестве основания и показателя степени. Некоторые числа могут давать большие результаты при возведении в степень, например, 2^10 = 1024, тогда как другие числа могут давать меньшие результаты, например, 2^(-2) = 1/4.
Использование основания степени может быть полезно в различных ситуациях. Например, при решении задач по физике, когда нужно вычислить площадь поверхности или объем объекта. Также это может быть полезно в управлении финансами или при работе с большими числами в программировании.
Теперь, когда вы знаете, что такое основание степени и как его использовать, вы можете экспериментировать с разными числами и степенями. И помните, что основание степени – это ключ к получению желаемого результата!
Показатель степени
Чтобы лучше понять, что такое показатель степени, давайте рассмотрим пример. Представьте, что у нас есть число 2, и нам нужно возвести его в степень. Если показатель степени равен 2, то результатом будет 2 умножить на 2, то есть 4. Если показатель степени равен 3, то результатом будет 2 умножить на 2, затем на 2, что даст нам 8.
Показатель степени обозначается с помощью верхнего индекса, который ставится после числа, являющегося основанием. Например, 2^3 означает число 2, возведенное в степень 3. В результате мы получим 8.
Теперь представьте, что мы имеем не только числа, но и переменные в выразлениях. Например, у нас есть выражение x^2. Это означает, что переменная x возводится в степень 2. Если, например, x=3, то x^2 будет равно 9.
Показатель степени может быть любым числом, в том числе и отрицательным. Например, 2^-2 означает, что число 2 возводится в отрицательную степень 2. В этом случае мы получим 1/4, так как отрицательная степень означает, что мы делим 1 на число, возведенное в положительную степень.
Теперь, когда вы знаете, что такое показатель степени и как его использовать, попробуйте решить несколько задач самостоятельно. Какая степень получится, если возведешь число 5 в 4-ю степень? Попробуйте посчитать и проверьте себя.
Как использовать основание и показатель степени?

Основание степени
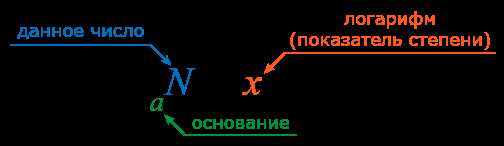
Основание степени — это число, которое возводится в степень. Оно может быть любым положительным числом, кроме нуля и единицы. Например, в выражении 2^3, число 2 является основанием степени.
Основание степени важно для определения значения выражения. Например:
- 2^0 = 1
- 2^1 = 2
- 2^2 = 4
- 2^3 = 8
Выражение 2^0 равно 1, так как любое число, возведенное в степень 0, равно 1. А выражение 2^1 равно самому основанию, то есть 2. Чем больше показатель степени, тем больше будет результат. Таким образом, зная основание степени, мы можем оперировать числами в виде степеней и решать различные задачи.
Показатель степени
Показатель степени — это число, которое показывает, сколько раз нужно перемножить основание степени. Он может быть любым целым числом, в том числе и отрицательным.
При положительном показателе степени мы перемножаем основание столько раз, сколько указано в показателе. Например:
- 2^3 = 2 * 2 * 2 = 8
- 3^4 = 3 * 3 * 3 * 3 = 81
При отрицательном показателе степени мы возводим основание в обратную величину показателя и получаем десятичную дробь. Например:
- 2^-2 = 1 / (2 * 2) = 1/4 = 0.25
- 10^-3 = 1 / (10 * 10 * 10) = 1/1000 = 0.001
Таким образом, показатель степени определяет, сколько раз нужно перемножить основание степени, чтобы получить результат. Он может быть как положительным, так и отрицательным.
Применение в практических задачах
Основание и показатель степени широко применяются в различных областях, включая физику, экономику, программирование и технические науки. Они позволяют упростить и ускорить вычисления, а также решать сложные задачи.
Например, в физике основание и показатель степени используются для определения мощности электрических цепей, экспоненциального роста и затухания величин, а также для моделирования различных физических процессов.
В экономике основание и показатель степени помогают анализировать темпы роста и падения различных показателей, таких как ВВП, инфляция и процентные ставки.
В программировании основание и показатель степени используются для работы с большими числами, оптимизации алгоритмов и решения математических задач.
Таким образом, основание и показатель степени являются важными инструментами для решения различных задач, их правильное использование позволяет упростить вычисления и получить точные результаты. Не бойтесь использовать их в своих расчетах и задачах, они сделают вашу жизнь намного проще!
Операции с основаниями и показателями степеней
Основание и показатель степени играют важную роль в работе с экспонентами. Поэтому необходимо знать, как выполнять операции с ними правильно.
Когда нужно сложить или вычесть степени с одинаковыми основаниями, мы просто складываем или вычитаем показатели: a^m + a^n = a^(m + n). Это правило действует только при условии, что основания степеней совпадают, и знаки показателей одинаковые.
Если основания степеней различаются, сложение или вычитание невозможны, но можно использовать свойства степеней для их переписывания в удобной форме. Например, a^m + b^m = (a^m)/(b^m).
Умножение степеней с одинаковым основанием происходит по правилу: a^m * a^n = a^(m + n). Это интуитивно понятно: если нам нужно перемножить несколько одинаковых чисел, мы просто складываем их показатели.
Также умножение может применяться к произведению степеней: (a^m) * (b^n) = (a * b)^(m + n). Снова, это правило основано на свойствах степеней.
Деление степеней с одинаковым основанием выполняется по правилу: (a^m)/(a^n) = a^(m — n). Как и в случае умножения, мы просто вычитаем показатели.
Если основания степеней различаются, деление невозможно, но с помощью свойств можно переписать выражение в другой форме, чтобы упростить его.
Наконец, возведение степени в степень осуществляется путем умножения показателей: (a^m)^n = a^(m * n). Здесь мы просто умножаем показатели, чтобы получить новый показатель степени.
Эти правила помогают упростить сложные выражения со степенями, делают работу с основаниями и показателями степеней более легкой и интуитивно понятной.
Основание и показатель степени: что это такое и как использовать?
Основание и показатель степени часто обозначаются как a и n соответственно. Их можно представить в виде a^n, где a — основание, а n — показатель степени. Когда число возведено в положительную целую степень, каждый раз число умножается само на себя. Например, 2^3 равно 2 * 2 * 2, что равно 8.
При использовании отрицательного показателя степени происходит обратная операция — число делится на себя само несколько раз. Например, 2^(-3) равно 1 / (2 * 2 * 2), что равно 1/8 или 0.125.
Также стоит отметить, что для любых оснований а и показателей степеней n, число a^0 будет равно 1. Это связано с тем, что когда число возводится в степень 0, оно равно 1.
Основание и показатель степени также могут быть представлены в виде таблицы, чтобы упростить их визуализацию и выполнение математических операций с ними. Ниже приведен пример таблицы с различными значениями основания и показателя степени:
| Основание | Показатель степени | Результат |
| 2 | 3 | 8 |
| 5 | 2 | 25 |
| 10 | -2 | 0.01 |
В таблице выше видно, что при возведении различных оснований в степень можно получить различные результаты. Это позволяет использовать основание и показатель степени для решения различных математических задач, например, для вычисления площади круга (где основание радиус, а показатель степени 2) или для расчета процентов (где основание число, а показатель степени процент).